A particle of mass m and charge q is lying at the origin in a uniform

A particle of mass m, carrying a charge q, is lying at the origin in a uniform magentic field directed along X axis. At the instant t = 0 it is given a velocity $v_{a}$ at an angle $θ$ with the y-axis, in the XY plane. The coordinates of the particle after two revolution will be

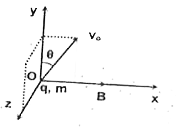A $(0, 0 \frac{2 π m v_{0} sin θ}{q B})$
B $(\frac{2 π m v_{0} sin θ}{q B}, 0, 0)$
C $(\frac{4 π m v_{0} sin θ}{q B}, 0, 0)$
D(0,0,0)
A charged particle is fired at an angle $θ$ to a uniform magnetic field directed along the x-axis. During its motionalong a helical path, the particle will
Anever move parallel to the x-axis
Bmove parallel to the x-axis once during every rotation for all velues of $θ$
Cmove parallel to the x-axis at least once during every rotation if $θ = 45^{\circ}$
Dnever move perpendicular to the x-direction
In a certain region uniform electric field E and magnetic field B are present in mutually opposite directions. At the instant $t = 0$ , a particle of mass m carrying a charge q is given velocity $v_{0}$ at angle $θ$ , with the $y -$ axis, in the yz plane. The time after which the speed of the particle would be minimum is equal to

A $\frac{m V_{0}}{q E}$
B $\frac{m V_{0} sin θ}{q E}$
C $\frac{m V_{0} cos θ}{q E}$
D $\frac{2 π m}{q B}$

A particle of mass $m$ and charge $q$ is lying at the origin in a uniform magnetic field $B$ directed along x-axis. At time t = 0, it is given a velocity $v_{0}$ , at an angle $θ$ with the y-axis in the xy-plane. Find the coordinates of the particle after one revolution.