If G,rA and rV denote the internal resistances of a galvanometer, an ammeter and a voltmeter among the following the correct relationship is
G<rA<rV
rA<rV<G
rA<G<rV
rV<rA<G
The correct Answer is:3
Step by step video, text & image solution for If G,r_(A) and r_(V) denote the internal resistances of a galvanometer, an ammeter and a voltmeter among the following the correct relationship is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - LEVEL-I(C.W)
58 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Level-II(C.W)
63 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE - 4
20 Videos
- MAGNETISM AND MATTERBOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
17 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-II-(H.W)
9 Videos
Similar Questions
Knowledge Check
Consider two identical galvanometers and two identical resistors with resistance R. If the internal resistance of the galvanometers Rc<R/2, which of the following statement(s) about any one of the galvanometers is (are) true?
AThe maximum voltage range is obtained when the two resistors and one galvanometer are connected in seriesBThe maximum voltage range is obtained when the two resistors and one galvanometer are connected in series , and the second galvanometer is connected in parallel to the first galvanometerCThe maximum current range is obtained when all the components are connected in parallelDThe maximum current range is obtained when the two galvanometers are connected in series and the combination is connected in parallel with both the resistorsThe value of resistance of an unknown resistor is calculated using the formula R=V/I where V and I are the readings of the voltmeter and the ammeter, respectivley. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RVandRG,respectively) are finite and nonzero.
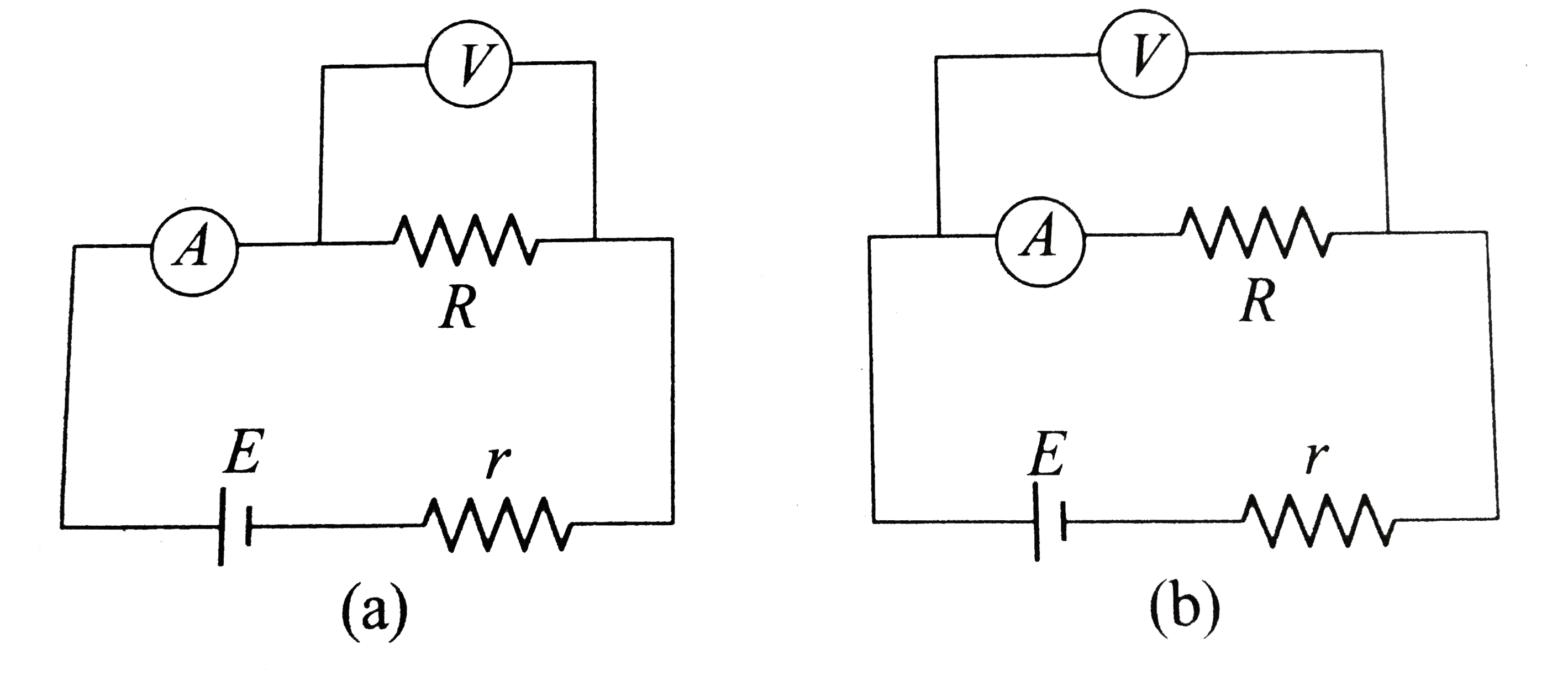 ,
,
Let RAandRB be the calculated values in the two cases A and B , respectively.
If the resistance of voltmeter is RV=1kΩ and the percentage error in the measurement of R (the value of R is nearly 10Ω)isAzero in both casesBnonzero but equal in both casesCmore in circuit ADmore in circuit BThe value of resistance of an unknown resistor is calculated using the formula R=V/I where V and I are the readings of the voltmeter and the ammeter, respectivley. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RVandRG,respectively) are finite and nonzero.
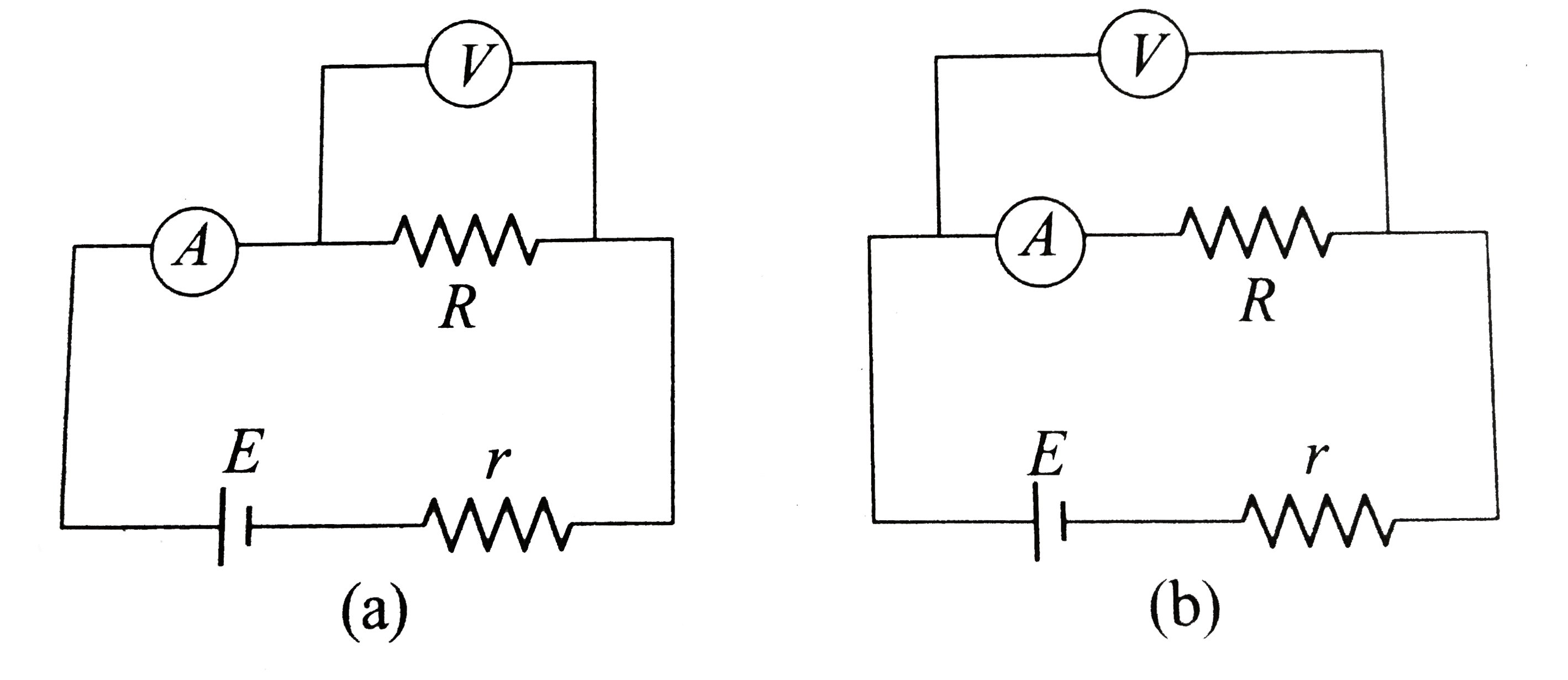 ,
,
Let RAandRB be the calculated values in the two cases A and B , respectively.
The relation between RA and the actual value of R isAR>RABR<RACR=RBDdependent upon E and r.
Resistance value of an unknown resistor is calculated using the formula R=VI where V and I be the readings of the voltmeter and the ammeter respectively. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RvandRGrespectively ) are finite and non zero.
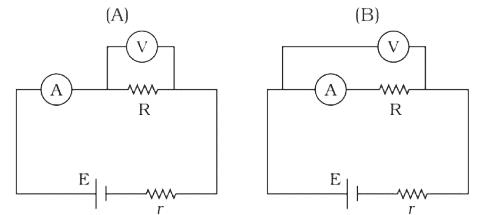
Let RvandRG be the calculated values in the two cases A and B respectively.
The relation between RBand the actual value of R is:
View SolutionResistance value of an unknown resistor is calculated using the formula R=VI where V and I be the readings of the voltmeter and the ammeter respectively. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RvandRBrespectively ) are finite and non zero.
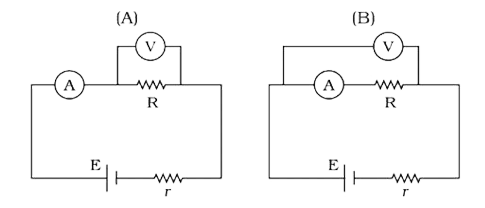
Let RAandRB be the calculated values in the two cases A and B respectively.
The relation between RA and the actual value R is
View SolutionResistance value of an unknown resistor is calculated using the formula R=VI where V and I be the readings of the voltmeter and the ammeter respectively. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RvandRGrespectively ) are finite and non zero.
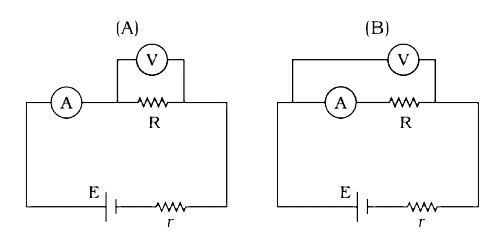
Let RvandRG be the calculated values in the two cases A and B respectively.
If the resistance of voltmeter is Rv=1kΩ and that of ammeter is RG=1Ω the magnitude of the percentage error in the measurement of R (the value of R is nearly 10Ω ) is:
View SolutionConsider the two circuits P and Q, shown below, which are used 20 measure the unknown resistance R.
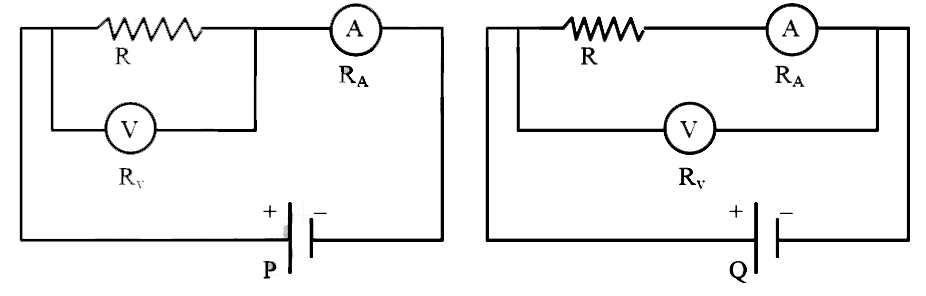
In each case, the resistance is estimated by using Ohm's law Rest=V/I, Where V and I are the readings of the voltmeter and the ammeter respectively. The meter resistances, Rv and RA are such that RA<<R<<Rv. The internal resistance of the battery may be ignored. The absolute error in the estimate of the resistance is denoted by δR=|R=Rest|.
View SolutionIf resistance of voltmeter is 10000Ω and resistance of ammeter is 2Ω then find R when voltmeter reads 12 V and ammeter reads 0.1 A
View Solution