Refer to the arrangement of charges in Fig and a Gaussian surface of radius R with Q at the centre. Then
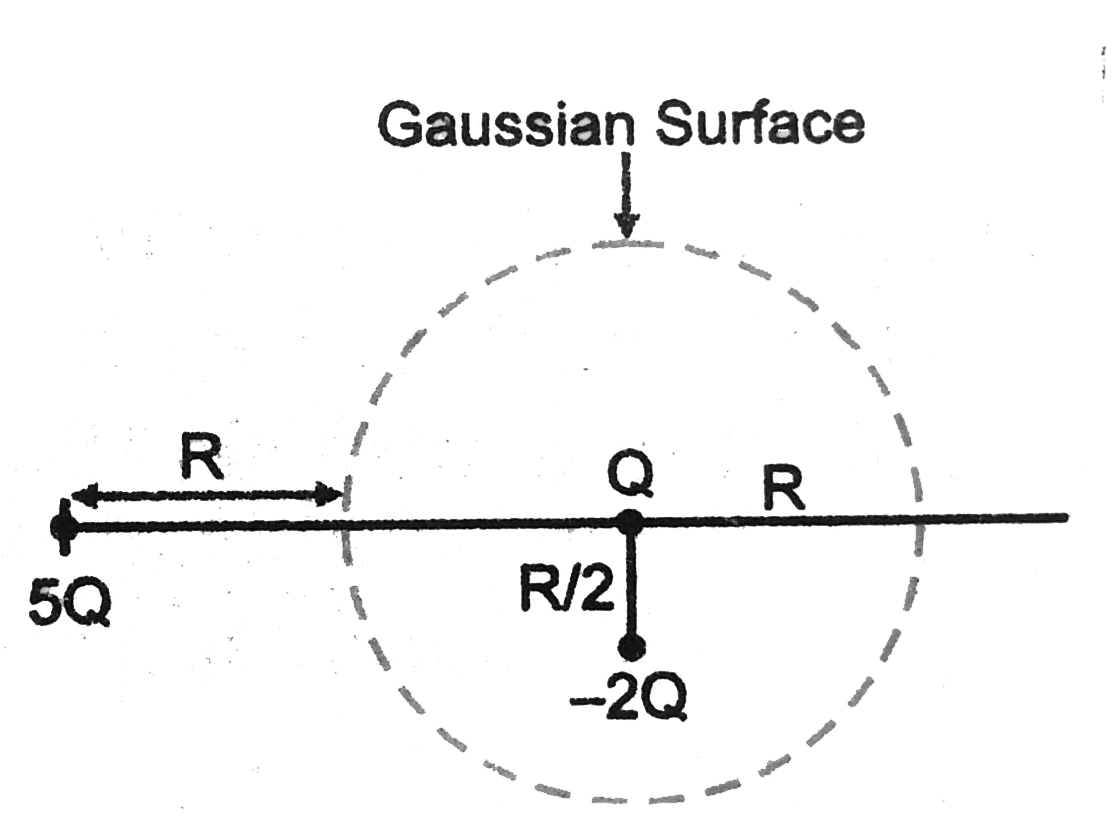
total flux through the surface of the spehre is −Qε0
field on the surface of the sphere is −Q4πε0R2
flux through the surface of sphere due to 5Q is zero.
field on the surface of spher due to −2Q is same everywhere.
The correct Answer is:A,C
Total charge enclosed by the gaussians surface is Q[=Q+(−2Q)] so total flux tough the surface is −Qε0 .As charge +5Q is outside the Gaussian surface the electric flux due ot it is zero .The electric field on the surface of the sphere is due to all the charges and is not consants beacuse the distribution of charges is not same for each and every point .
Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level V
Explore 93 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Passage I
Explore 3 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level 3
Explore 22 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:ADDITIONAL PROBLEMS
Explore 14 Videos
- EXPERIMENTAL PHYSICSBook:NARAYNAChapter:EXPERIMENTAL PHYSICSExercise:Comprehension type
Explore 6 Videos
Similar Questions
Knowledge Check
The work done in carrying a charge q once around a circle of radius r with a charge Q placed at the centre centre will be
AQq4πε0r2BQq4πε0rCzeroDQq24πε0rThe work done in carrying a charge q once around a circle of radius r with a charge Q placed at the centre centre will be
AQq4πε0r2BQq4πε0rCzeroDQq24πε0rThe work done in carrying a charge Q1 once round a circle of radius R with a charge Q2 at the centre is
AQ1Q24π∈0R2BzeroCQ1Q24π∈0RDinfinite
A solid insulating sphere of radius a carries a net positive charge 3Q, uniformly distributed throughout its volume. Concentric with this sphere is a conducting spherical shell with inner radius b and outer radius c and having a net charge -Q, as shown in figure

a. Consider a spherical Gaussian surface of radius rgtc, the net charge enclosed by this surface is .............
b. The direction of the electric field rgtc is .............
c. The electric field at rgtc is ............... .
d. The electric field in the region with radius r, which cgtrgtb, is ...............
e. Consider a spherical Gaussian surface of radius r, where c>r>b, the net charge enclosed by this surface is ................ .
f. Consider a spherical Gaussian surface of radius r, whereb>r>a, the net charge enclosed by this surface is ................. .
g. The electric field in the region b>r>a is ................ .
h. Consider a spherical Gaussian surface of radius r<a. Find an expression for the net charge Q(r) enclosed by this surface as a function of r. Note that the charge inside the surface is less than 3Q.
i. The electric field in the region r<a is ................. .
j. The charge on the inner surface of the conducting shell is .......... .
k. The charge on the outer surface of the conducting shell is .............. .
l. Make a plot of the magnitude of the electric field versus r.
View SolutionA charge of 8.85C is placed at the centre of a spherical Gaussian surface of radius 5cm .The electric flux through the surface ..
View SolutionAn infinite, uniformly charged sheet with surface charge density σ cuts through a spherical Gaussian surfance of radius R at a distance X from its center, as shown in the figure. The electric flux Φ through the Gaussian surfce is .

View Solutionq1,q2,q3 and q4 are point charges located at point as shown in the figure and S is a spherical Gaussian surface of radius R. Which of the following is true according to the Gauss's law

View SolutionAssertion:- In a given situation of arrangement of charges, an extra charge is placed outside the Gaussion surface. In the Gauss Theroem
∮→Ed→s=Q∈ε0Q∈ remains unchanged whereas electric field →E at the site of the element is changed.
Reason:- Electric field →E at any point on the Gaussian surface is due to inside charge only.
View Solution
