the electric field is given by →E=→Fq0 here the test charge q0 should be (a) Infinitesimally small and positive
(b) Infintestimally small and negative
only a
only b
a (or) b
neither a and b
The correct Answer is:A
Step by step video, text & image solution for the electric field is given by vec(E)=(vec(F))/(q_(0)) here the test charge q_(0) should be (a) Infinitesimally small and positive (b) Infintestimally small and negative by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level 1(C.W)
Explore 24 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level II(C.W)
Explore 27 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Intergers type question
Explore 11 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:ADDITIONAL PROBLEMS
Explore 14 Videos
- EXPERIMENTAL PHYSICSBook:NARAYNAChapter:EXPERIMENTAL PHYSICSExercise:Comprehension type
Explore 6 Videos
Similar Questions
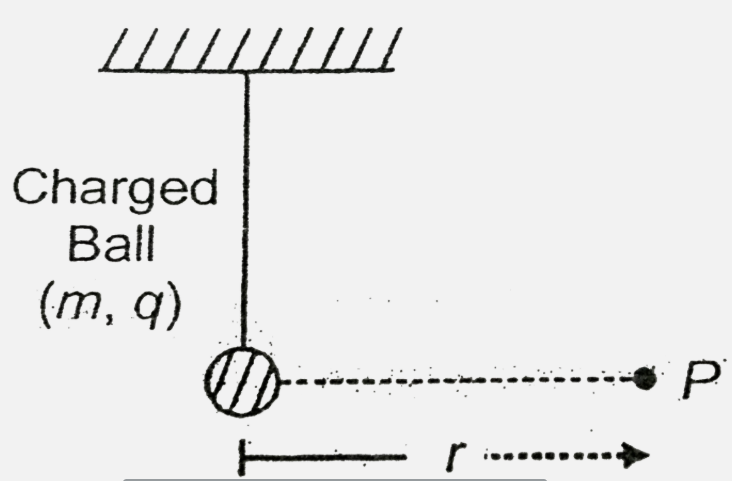
The electric field at point P due to a charged ball is given by
Ep=14πε0qr2
To measure 'E' at point P, A test charge q0 is placed at point P and measure electric force F upon the test charge. Check whether Fq0 is equal to 14πε0qr2 or not .
View SolutionAn electric field is defined in terms of q0 a small positive charge. If the definition was in terms of a small negative charge of the same magnitude, then compared to the original field the newly defined electric field.
(a) would point in the same direction and have the same magnitude.
(b) would point in the opposite direction and have the same magnitude.
(c ) would point in the same direction and have the different magnitude.
(d) would point in the opposite direction and have the different magnitude.
View Solution
Knowledge Check
the electric field is given by →E=→Fq0 here the test charge q0 should be (a) Infinitesimally small and positive
(b) Infintestimally small and negativeAonly aBonly bCa or bDneither a or bIf electric field around a surface is given by ∣∣→E∣∣=Q∈ε0|A| where 'A' is the normal area of surface and Q∈ is the charge enclosed by the surface. This relation of gauss's law is valid when
ASurface is equipotentialBMagnitude of electric field is constantCMagnitude of electric field is constant & the surface is equipotentialDFor all Gaussian surfaces.Force →F acting on a test charge q0 in a uniform electric field →E is
A→F=q0→EB→F=→Eq0C→F=q0→ED→F=q20→E
A particle having mass m and charge q is released from the origin in a region in which electric field and megnetic field are given by →B=−B0ˆj and →E=→E0ˆk. Find the speed of the particle as a function of its z-coordinate.
View SolutionAn infinite sheet in xy plane has a uniform surface charge density σ. The thickness of the sheet is infinitesimally small. The sheet begins to move with a velocity →v=vˆi
(i) Find the electric field (→E) and magnetic field (→B) above and below the sheet.
(ii) If the velocity of the sheet is changed to →v=vˆk , find the electric and magnetic field above and below the sheet.
View SolutionA charge Q located at a point →r is in equilibrium under the combined field of three charges q1,q2 and q3. If the charges q1 and q2 are located at point →r1 and →r2 respectively, find the direction of the force on Q due to q3 in terms of q1,(q2),→r1→r2, and →r.
View SolutionForce →F acting on a test charge q0 in a uniform electric field →E is
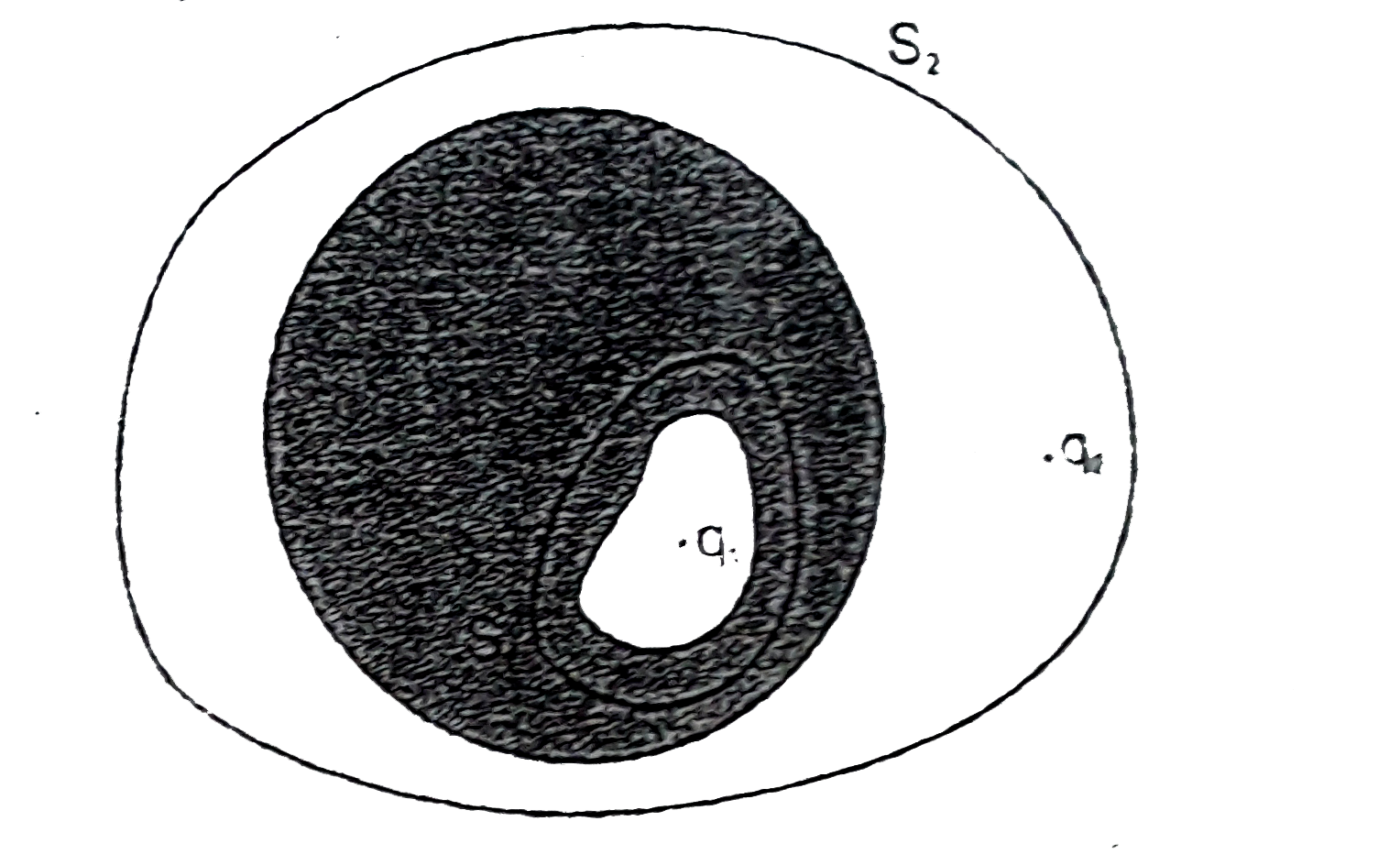
View SolutionFigure shows a conducting sphere with a cavity. A point charge q1 is placed inside cavity, and q2 is placed out side the sphere →Ein is electric field due to charge induced on surface of cavity. →Eout is electric field due to charge induced on outer surface of sphere and →Enet is net field at any point. Two closed gaussian surface S1 & S2 are also drawn in the figure.
View Solution

