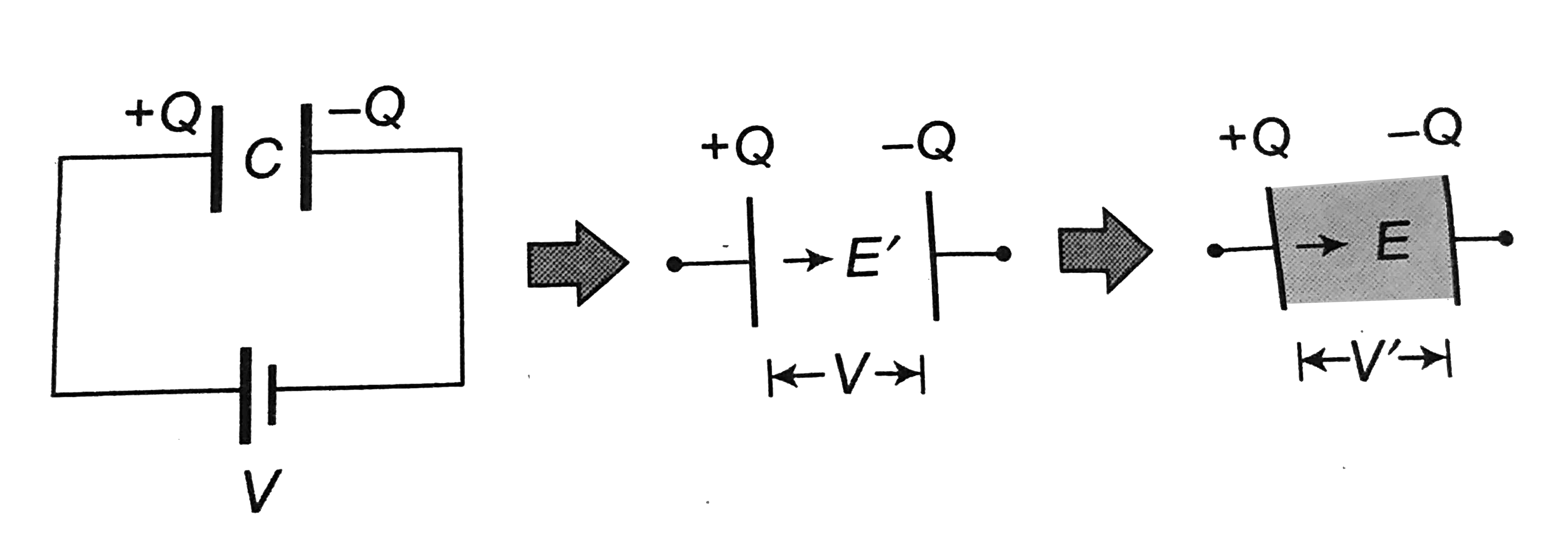
A parallel plate capacitor of plate area A and plate separation d is charged to potential difference V and then the battery is disconnected. A slab of dielectric constant K is then inserted between the plates of the capacitor so as to fill the space between the plates. If Q, E and W denote respectively, the magnitude of charge on each plate, the electric field between the plates (after the slab is inserted), and work done on the system, in question, in the process of inserting the slab, then

A

$Q = \frac{A \in_{0} V}{d}$

B

$\frac{K A \in_{0} V}{d}$

C

$E = \frac{V}{K d}$

D

$W = \frac{1}{2} \frac{A \in_{0} V^{2}}{d} (1 - \frac{1}{K})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$C = \frac{A \in_{0}}{d}, Q = C V = \frac{A \in_{0} V}{d}$
Charge remains same, $(A)$ is O.K.
$C V = K C V' \Rightarrow V' = \frac{V}{K}$
$E = \frac{V'}{d} = \frac{v}{K d}, (c)$ is O.K.
$W_{1 \to 2} = | U_{2} - U_{1} | = ∣ ∣ ∣ \frac{Q^{2}}{2 K C} - \frac{Q^{2}}{2 C} ∣ ∣ ∣$
$= \frac{1}{2} \frac{A \in_{0} V^{2}}{d} (1 - \frac{1}{K}), (D)$ is O.K.

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
In a parallel-plate capacitor of plate area $A$ , plate separation $d$ and charge $Q$ the force of attraction between the plates is $F$ .
A $F \propto Q^{2}$
B $F \propto \frac{1}{A}$
C $F \propto d$
D $F \propto \frac{1}{d}$
Question 2 - Select One
Figure shows a parallel plate capacitor with plate area $A$ and plate separation $d$ . A potential difference is being applied between the plates. The battery is then disconnected and a dielectric slab of dieletric constant $K$ is placed in between the plates of the capacitor as shown.

The electric field in the gaps between the plates and the electric slab will be
A $\frac{ε_{0} A V}{d}$
B $\frac{V}{d}$
C $\frac{K V}{d}$
D $\frac{V}{d - t}$
Question 3 - Select One
Figure shows a parallel plate capacitor with plate area $A$ and plate separation $d$ . A potential difference is being applied between the plates. The battery is then disconnected and a dielectric slab of dielectric constant K is placed in between the plates of the capacitor as shown.

The electric field in the dielectric slab is
A $\frac{V}{K d}$
B $\frac{K V}{d}$
C $\frac{V}{d}$
D $\frac{K V}{t}$

CP SINGH-CAPACITANCE-Exercise

Home
Ask Doubt
Profile