Calculate the distance in (Å) for given compound if bond length is 2.35Å.
The correct Answer is:
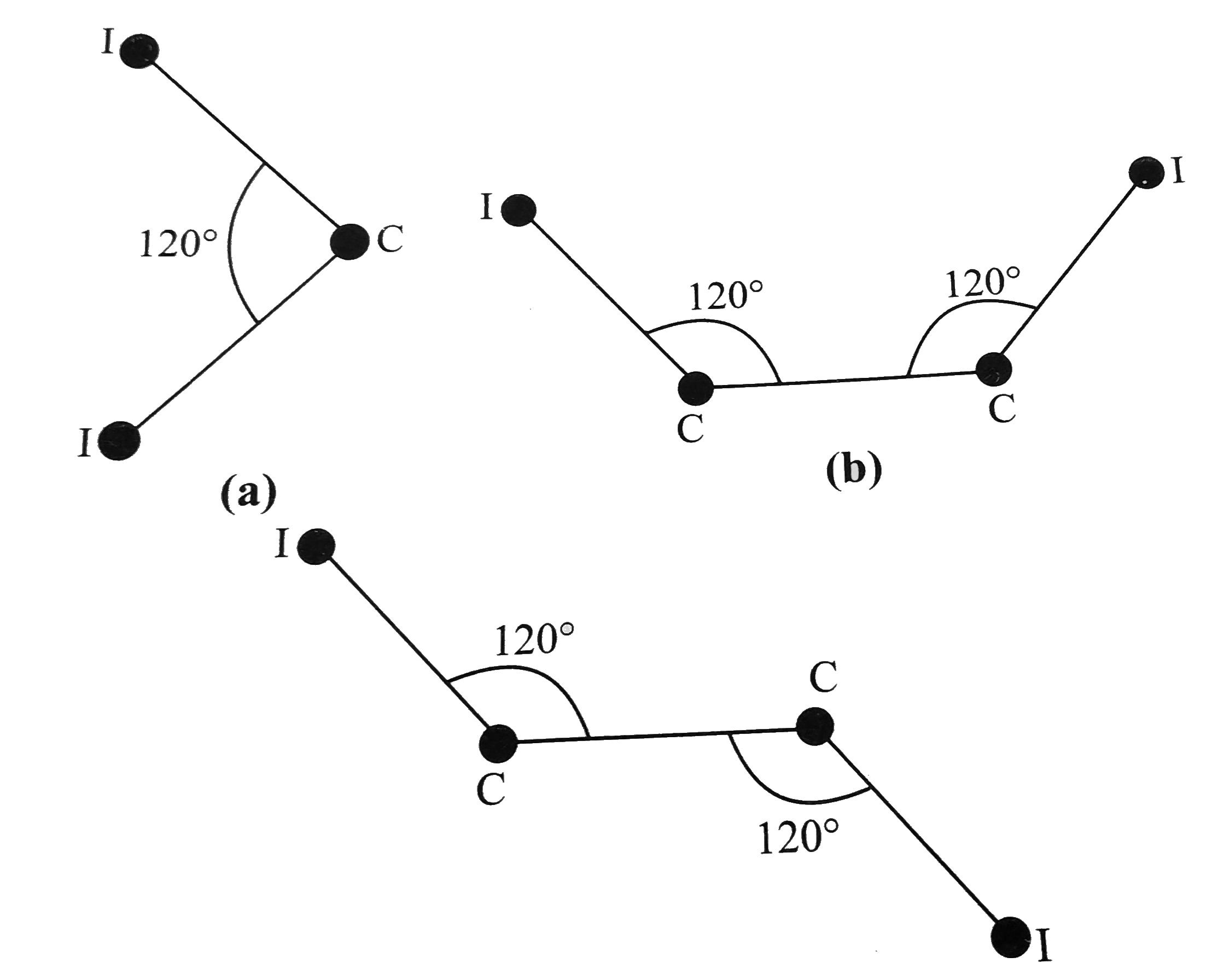
To calculate the I−I distance in the compound H₂C₂I₂, given that the C−I bond length is 2.35 Å, we can follow these steps:
Step 1: Understand the Molecular Geometry
The compound H₂C₂I₂ has a structure where each carbon is bonded to two iodine atoms. The carbon atoms are sp² hybridized, which means the bond angles around each carbon are approximately 120 degrees.
Step 2: Draw the Structure
Draw the structure of H₂C₂I₂. Each carbon atom is at the center of a triangle formed with the two iodine atoms. The bond angle between the two C−I bonds is 120 degrees.
Step 3: Identify the Relevant Triangle
In the triangle formed by the C−I bonds, we can denote:
- C as the carbon atom,
- I₁ and I₂ as the two iodine atoms.
The angle between the two C−I bonds (∠I₁CI₂) is 120 degrees. To find the distance between the two iodine atoms (I−I), we can drop a perpendicular from the carbon to the line joining the two iodine atoms, creating two right triangles.
Step 4: Calculate the Length of IO
We can denote:
- CI as the bond length (2.35 Å),
- IO as the distance from the carbon to the midpoint of the I−I bond.
Using the sine function in the triangle:
- The angle ICO (where O is the midpoint of I−I) is half of 120 degrees, which is 60 degrees.
Using the sine definition:
\(
\sin(60^\circ) = \frac{IO}{CI}
\)
Substituting the known values:
\(
0.866 = \frac{IO}{2.35}
\)
Now, solving for IO:
\(
IO = 0.866 \times 2.35
\)
Calculating this gives:
\(
IO \approx 2.035 \, \text{Å}
\)
Step 5: Calculate the I−I Distance
Since IO is the distance from carbon to the midpoint of the I−I bond, the total I−I distance is:
\(
I-I = 2 \times IO = 2 \times 2.035 \approx 4.07 \, \text{Å}
\)
Final Answer
The I−I distance in H₂C₂I₂ is approximately 4.07 Å.
---
The compound H₂C₂I₂ has a structure where each carbon is bonded to two iodine atoms. The carbon atoms are sp² hybridized, which means the bond angles around each carbon are approximately 120 degrees.
Draw the structure of H₂C₂I₂. Each carbon atom is at the center of a triangle formed with the two iodine atoms. The bond angle between the two C−I bonds is 120 degrees.
In the triangle formed by the C−I bonds, we can denote:
- C as the carbon atom,
- I₁ and I₂ as the two iodine atoms.
We can denote:
- CI as the bond length (2.35 Å),
- IO as the distance from the carbon to the midpoint of the I−I bond.
- The angle ICO (where O is the midpoint of I−I) is half of 120 degrees, which is 60 degrees.
\(
\sin(60^\circ) = \frac{IO}{CI}
\)
Substituting the known values:
\(
0.866 = \frac{IO}{2.35}
\)
Now, solving for IO:
\(
IO = 0.866 \times 2.35
\)
Calculating this gives:
\(
IO \approx 2.035 \, \text{Å}
\)
Since IO is the distance from carbon to the midpoint of the I−I bond, the total I−I distance is:
\(
I-I = 2 \times IO = 2 \times 2.035 \approx 4.07 \, \text{Å}
\)
The I−I distance in H₂C₂I₂ is approximately 4.07 Å.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Consider the statement ltbrlt I. Bond length in N+2 is 0.02Å greater than in N2.
II. Bond length of NO+ is 0.09Å less than in NO.
III O2−2 has shorter bond length than O2.
Which of the following statements are true?AI and IIBII and IIICI , II and IIIDI and IIIConsider the statements :
I . Bond length in N+2is0.002Å greater than in N2
II. Bond length in NO+is0.09Å less than in NO
III. O2−2 has shorter bond length than O2
which of the following statements are ture ?AI and IIBII and IIICI, II and IIIDI and III
Write the IUPAC names of the following compounds :
(i) (CH3)2C(C2H5)2
(ii)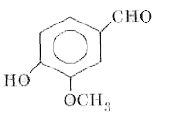
View SolutionCalculate the bond order in
(i) H+2 (ii) H−2andH2−2 have the same bond order?
View SolutionCalculate the enthalpy change for the reaction H2(g)+I2(g)→2HI(g)
Given that the bond energies of H-H,I-I and H-I are433, 151 and 299 kJmol−1 respectively.
View SolutionExplain the observations that the bond length in N+ is 0.02Å larger than in N2 while the bond length in NO+ is 0.09Å less than in NO.
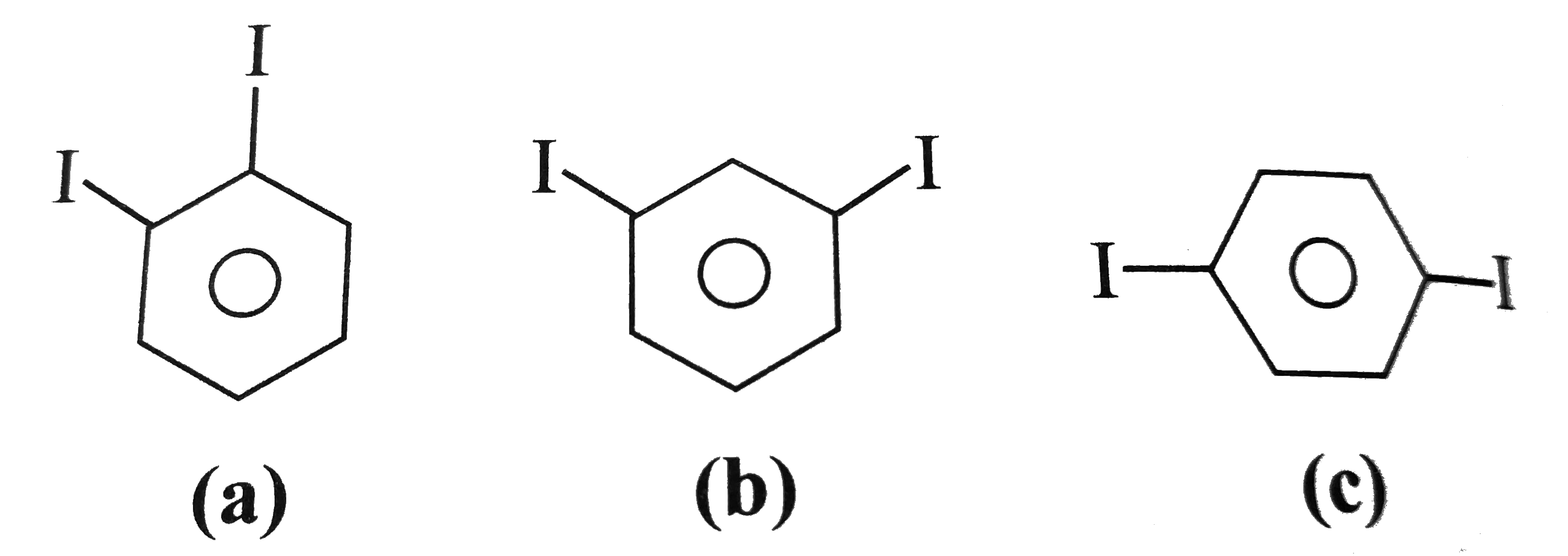
View SolutionCalculate the I-I distance in each of the three isomeric diiodobenzenes Assume that the ring is a regular hexagon and that each C−I bonds lies on a line through the centre of the hexagon .
Given C−I bond length =210 pm
The distance between two adjacent C-atom (i.e C-C)
=140 pm
 .
.
View SolutionCalculate the bond length of C−X bond, if C−C bond length is 1.54Å,X−X bond length is 1.00Å and electronegativity values of C and X are 2.0 and 3.0 respectively.
View Solution


 .
.