Points A and B lie on the parabola y = 2x^2 + 4x

The mid-point of the line-segment AB is P(0,4). If the coordinates of B are (-2, 3) then the co-ordinates of A are
A(2,5)
B3
C $\frac{13}{2}$
D $- \frac{13}{2}$
The mid-point of the line segment joining the points (- 2, 4) and (6, 10) is
A(2, 5)
B(2, 7)
C(3, 7)
D(3, 8)
In the figure P(3, 2) is the mid-point of the line segment AB. What are the co-ordinates of A and B respectively:

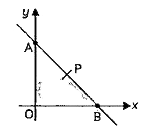A(4,0) and (6, 0)
B(0,4) and (6,0)
C(0,4) and (0,6)
D(0,-4) and (-6, 0)

Points $A$ and $B$ lie on the parabola $y = 2 x^{2} + 4 x - 2,$ such that origin is the mid-point of the line segment $A B .$ If $I$ be the length of the line segment $A B,$ then find the unit digit of $l^{2} .$