The two points on the line x+y=4that at a unit perpendicular distance from the line lie 4x+3y=10 are (a1,b1) and (a2,b2), then a1+b1+a2+b2
5
6
7
8
The correct Answer is:D
Step by step video & text solution for The two points on the line x +y =4 that at a unit perpendicular distance from the line lie 4x +3y =10 are (a_1, b_1) and (a_2, b_2), then a_1+ b_1+a_2+ b_2 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- STRAIGHT LINES BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - STRAIGHT LINES EXERCISE - Exercise-2 : One or More than One Answer is/are Correct
12 Videos
- STRAIGHT LINES BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - STRAIGHT LINES EXERCISE - Exercise-3 : Comprehension Type Problems
4 Videos
- SOLUTION OF TRIANGLESBOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-5 : Subjective Type Problems
12 Videos
- TRIGONOMETRIC EQUATIONS BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - TRIGONOMETRIC EQUATIONS EXERCISE - Exercise-5 : Subjective Type Problems
9 Videos
Similar Questions
Knowledge Check
If the equation of the locus of a point equidistant from the points (a1,b1) and (a2,b2) is (a1−a2)x+(b2+b2)y+c=0, then the value of C is
Aa21−a22+b21−b22B√a21+b21−a22−b22C12(a21+a22+b21+b22)D12(a21+b22+a21+b22)The capacitance of the capacitors of plate areas A1 and A2(A1<A2) at a distance d is
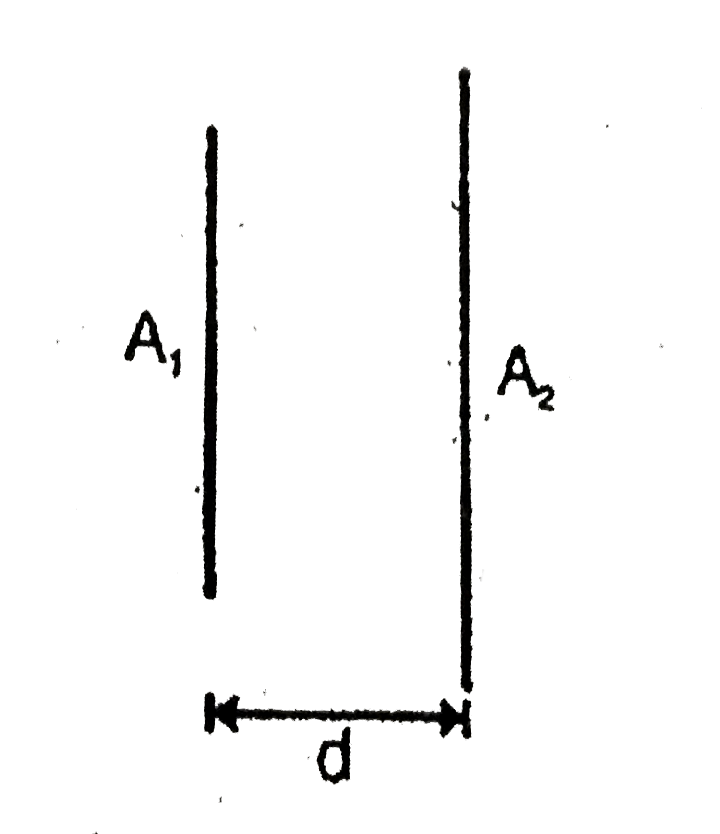 Aε0A1dBε0A2dCε0(A1+A2)2dDε0√A1A2d
Aε0A1dBε0A2dCε0(A1+A2)2dDε0√A1A2d
Let →a=a1ˆi+a2ˆj+a2ˆk,→b=b1ˆi+a2ˆj+b2ˆk,and→c=c1ˆi+c2ˆj+c2ˆk, be three non-zero vectors such that →c is a unit vector perpendicular to both vectors →aand→b . If the angle between aandb is π/6, then |a1a2a3b1b2b3c1c2c3|2 is equal to 0 1 14(a12+a22+a32)(b12+b22+b32) 34(a12+a22+a32)(b12+b22+b32)(c12+c22+c32)
View SolutionLet →a=a1ˆi+a2ˆj+a3ˆk;→b=b1ˆi+b2ˆj+b3ˆk;→c=c1ˆi+c2ˆj+c3ˆk be three non-zero vectors such that →c is a unit vector perpendicular to both →a&→b. If the angle between →aand→b is π6 , then ∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣2=
View SolutionIn direct proportion a1b1 = a2b2
View Solutiona1,a2,a3,∈R−{0} and a1+a2cos2x+a3sin2x=0forallx∈R, then (a)vector →a=a1ˆi+a2ˆj+a3ˆkand→b=4ˆi+2ˆj+ˆk are perpendicular to each other (b)vector →a=a1ˆi+a2ˆj+a3ˆkand→b=−ˆi+ˆj+2ˆk are parallel to each other (c)vector →a=a1ˆi+a2ˆj+a3ˆk is of length√6 units, then one of the ordered triple (a1,a2,a3)=(1,−1,−2) (d)are perpendicular to each other if 2a1+3a2+6a3=26,then∣∣a1ˆi+a2ˆj+a3ˆk∣∣is2√6
View SolutionIf the tangent and normal to xy=c2 at a given point on it cut off intercepts a1,a2 on one axis and b1,b2 on the other axis, then a1a2+b1b2= (A) −1 (B) 1 (C) 0 (D) a1a2b1b2
View SolutionIf amˆi+bmˆj+cmˆk m=1,2,3 are pairwise perpendicular unit vectors then ∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣ is equal to
View Solution
