If the minimum value of the quadratic expression y=ax2+bx+c is negative attained at negative vlaue of x, then :
a>0
b>0
c>0
D>0
The correct Answer is:A, B, D
Step by step video, text & image solution for If the minimum value of the quadratic expression y =ax ^(2)+bx +c is negative attained at negative vlaue of x, then : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRATIC EQUATIONS Book:VIKAS GUPTA (BLACK BOOK)Chapter:QUADRATIC EQUATIONS Exercise:EXERCISE (COMPREHENSION TYPE PROBLEMS)
Explore 23 Videos
- QUADRATIC EQUATIONS Book:VIKAS GUPTA (BLACK BOOK)Chapter:QUADRATIC EQUATIONS Exercise:EXERCISE (MATCHING TYPE PROBLEMS)
Explore 1 Video
- QUADRATIC EQUATIONS Book:VIKAS GUPTA (BLACK BOOK)Chapter:QUADRATIC EQUATIONS Exercise:EXERCISE (SUBJECTIVE TYPE PROBLEMS)
Explore 45 Videos
- PROBABILITY Book:VIKAS GUPTA (BLACK BOOK)Chapter:PROBABILITY Exercise:Exercise -5 : Subjective Type problems
Explore 12 Videos
- SEQUENCE AND SERIES Book:VIKAS GUPTA (BLACK BOOK)Chapter:SEQUENCE AND SERIES Exercise:EXERCISE (SUBJECTIVE TYPE PROBLEMS)
Explore 21 Videos
Similar Questions
Knowledge Check
The quadratic expression ax2+bx+c>0∀x∈R, then :
A13a−5b+2c>0B13a−b+2c>0Cc>0,D<0Da+c>b,D<0The values of 'a' for which the quadraic expression ax2+(a−2)x−2 is negative for exactly two integral values of x, belongs to
A[−1,1]B[1,2)C[−1,1]D[-2,-1])For which of the following graphs the quadratic expression y=ax2+bx+c the product abc is negative ?
A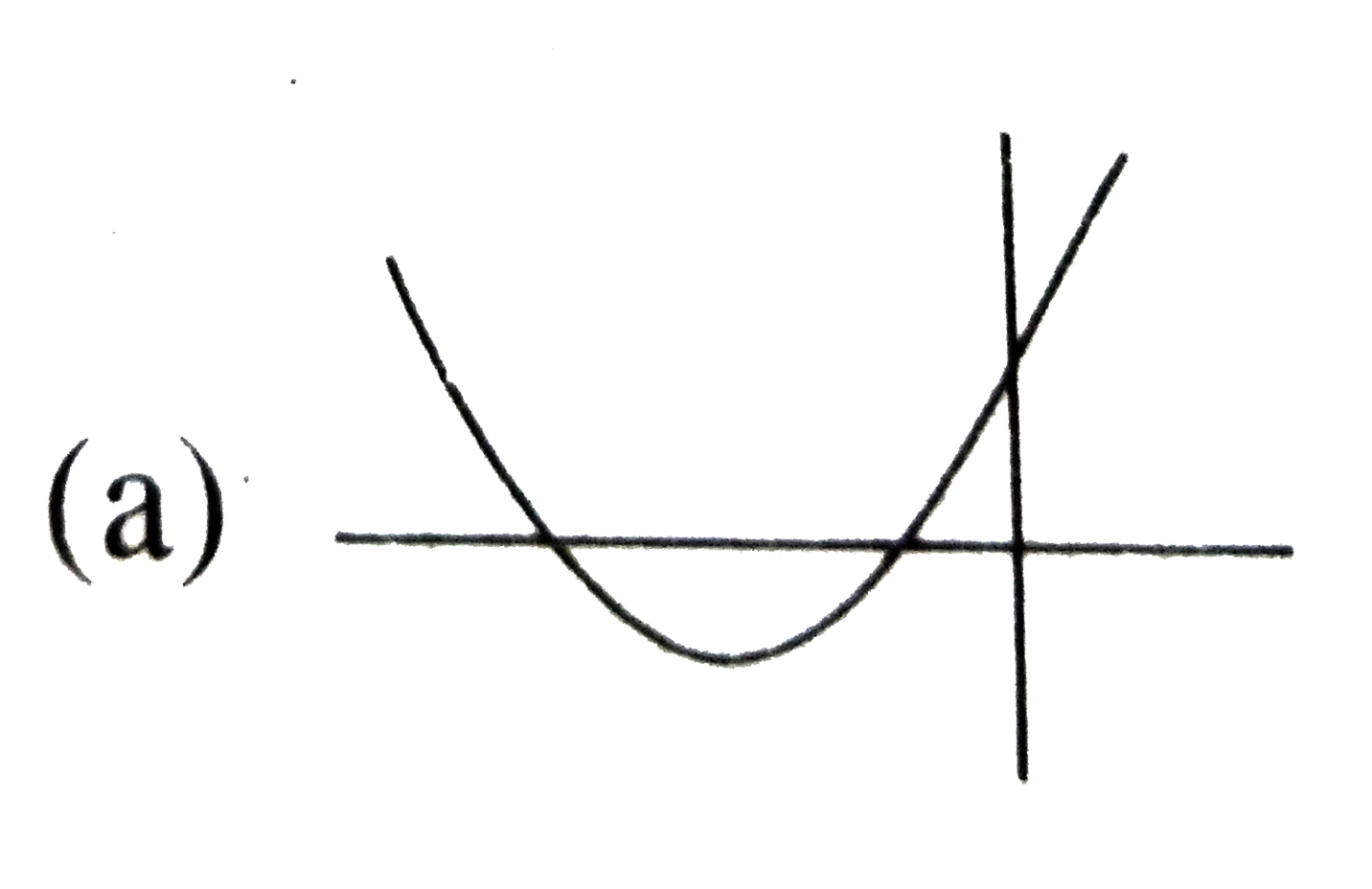 B
B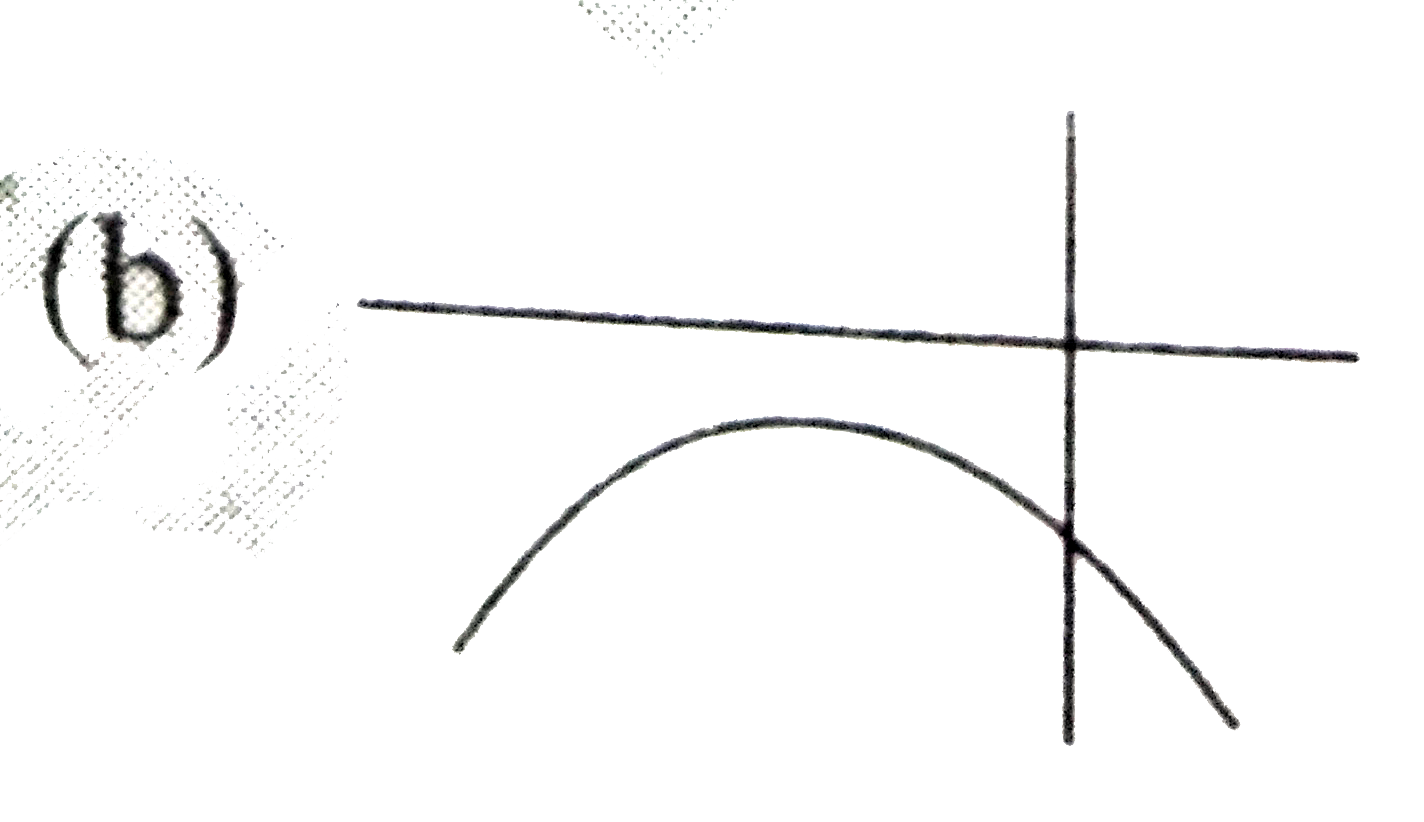 C
C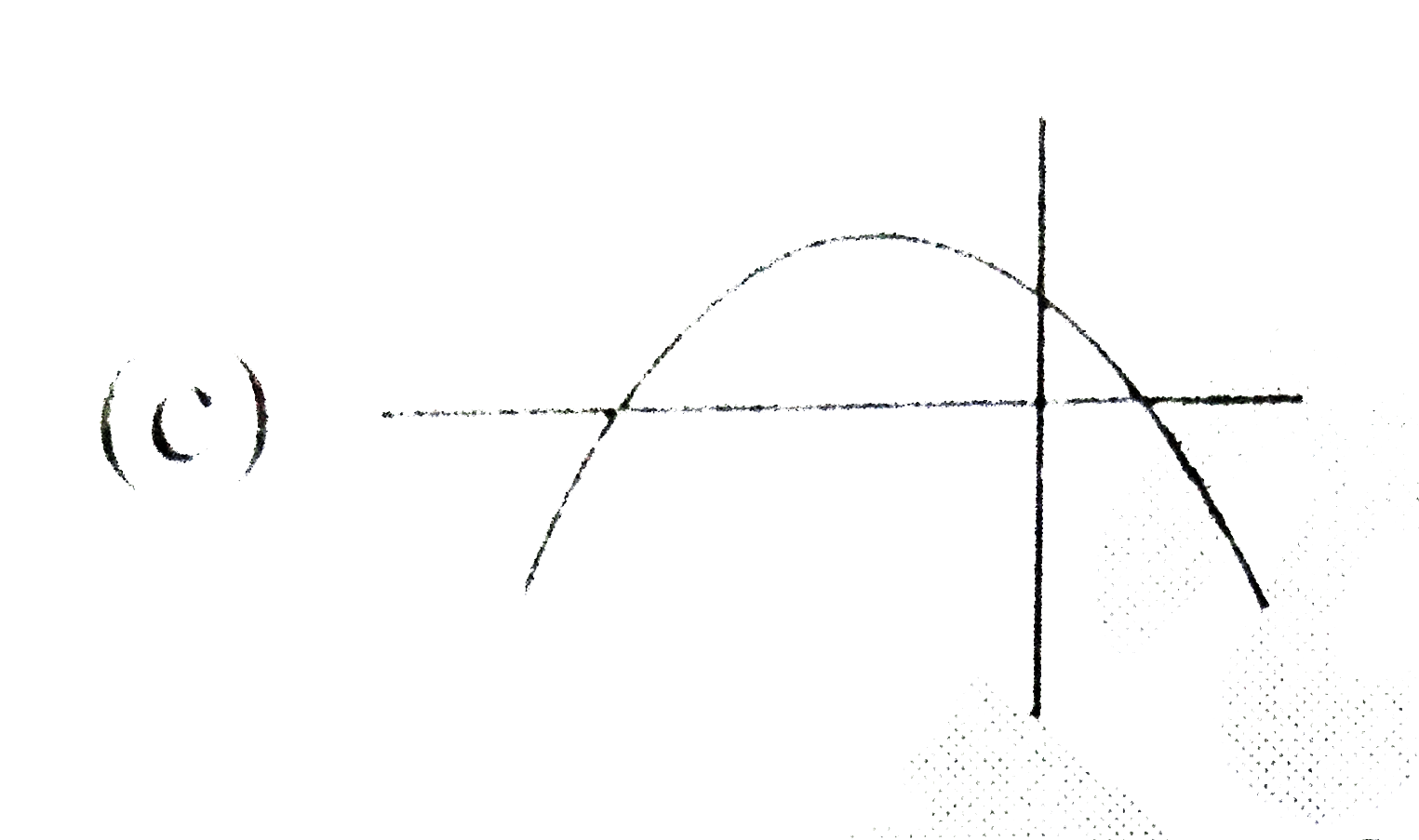 D
D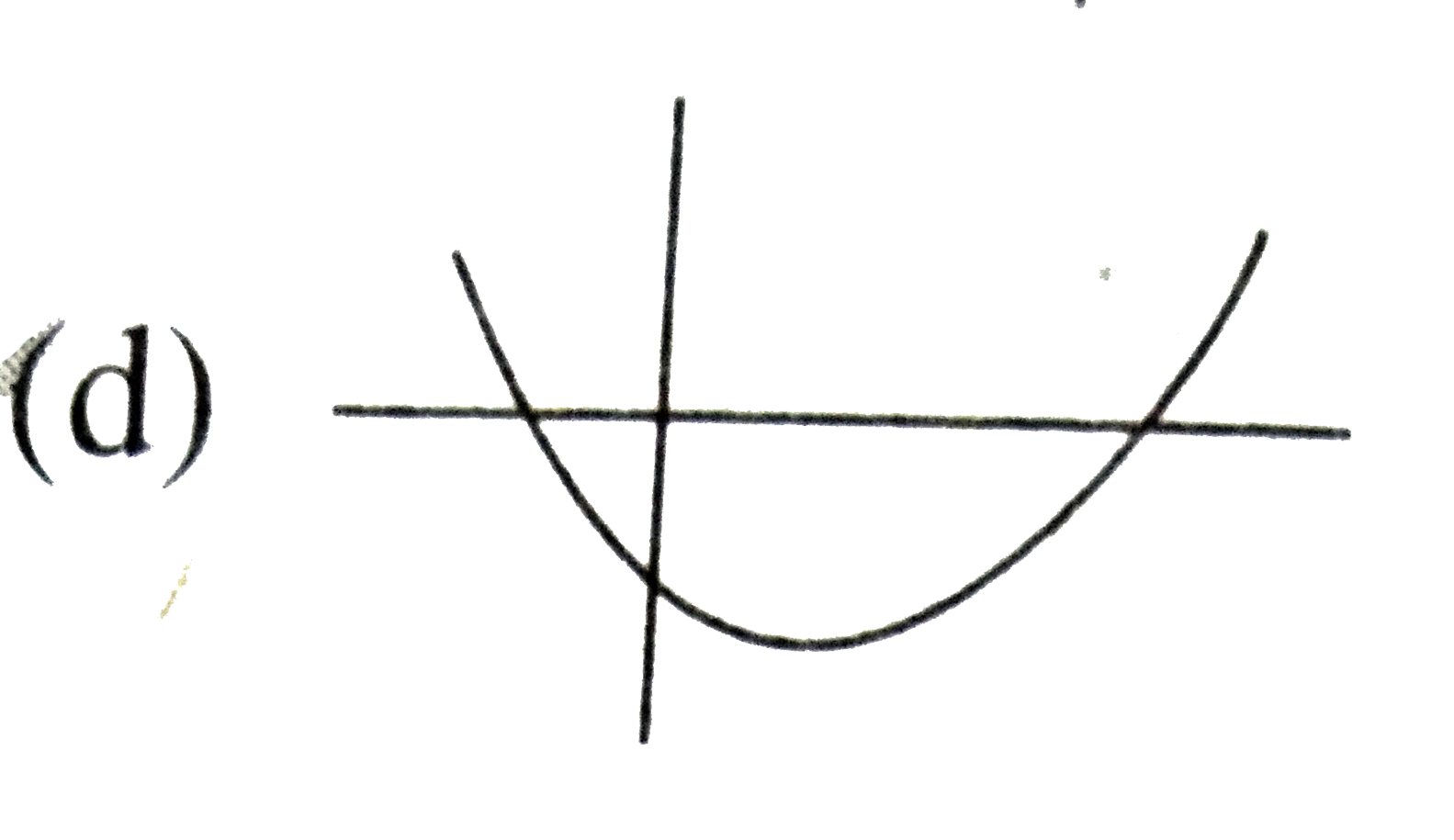
The quadratic expression ax2+bx+c>0 ∀x∈R ,then
View SolutionPlease explain Range of quadratic expression f(x)=ax2+bx+c
View SolutionThe values of 'a' for which the quadraic expression ax2+(a−2)x−2 is negative for exactly two integral values of x, belongs to
View SolutionIf a and b are the maximum and minimum values of the quadratic expressions 1−2x−5x2 and x2−2x+5 respectively then the set of the all values of x for which the expression 5ax2+bx+7 is positive
View SolutionIf graph of the quadratic y=ax2+bx+c is given below :
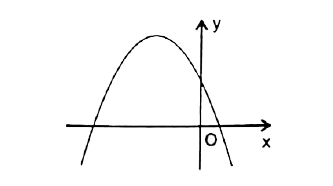 then:
then:
View Solution
