Cube
Cube
In the Geometry section of the mathematics, one interesting concept is the concept of cube, which is a solid three-dimensional figure. A cube will have 6 square faces, 8 vertices and 12 edges. The cube can also be considered as a regular hexahedron.
In your normal daily life when dealing with puzzle games, you might have at some point of time could come across a 3 × 3 Rubik's cube. It is one of the best examples of a cube that you must have seen in real life. The Rubik's cube helps solve puzzles that sharpen your mind through posing organizing challenges. In real life, you could see many other cube examples which are used or involved in solving puzzles. One such example other than a Rubik's cube is the 6 sided dice and such others.
The part or section of Geometry that discusses these cubes is called as the Solid Geometry. Solid geometry is all about considering the three-dimensional shapes and/or figures. And these have surface areas and volumes.
We have already discussed in the earlier section that a cube is a 3-Dimensional figure having six sides. In addition to that, the cube-shaped object has 8 vertices and 12 edges. This phenomenon is such that the cube will have 3 edges that meet at only one vertex point. The cube cal also is known as a square parallelepiped. This cube-shaped object is also known as an equilateral cuboid and/ or a right rhombohedron.
By observing the figure given above, the cube will have edge, face and vertex. While L represents the length, B represents the breadth, and finally, H represents the height of the cube-shaped object. There are these edges of the cube which are connecting at a single point which is called as the vertex of the cube.
Normally, the face of a cube is connected by usually four vertices. In addition to these properties of the cube, we look at the formulae for the surface area and also the volume of the cube.
Until now, in the previous sections, we have discussed in detail about the cube definition, various types of cubes, their properties and distinguishing characteristics. Now, we will look at the formulae that help us in finding the Surface Area and Volume for Cube.
Surface Area of Cube
We can easily recognize that for any shaped object, the area of that shaped object is clearly defined as the region that stays occupied by that shape in the plane. Since the cube is a 3D object which is three dimensional, the area occupied by the cube will be in a 3-Dimensional plane-shaped object. Moreover, the cube shape object will be having a total of 6 faces. Hence, the calculation of the surface area of the cube will involve finding out the surface area of the cube for each and every face of the total six faces.
Thus, the formula for calculating the surface area of the cube will be derived as:
Surface area of the cube = 6a2, which will be in square units.
Volume of Cube
The volume of the cube is represented by the total space contained in the cube. Supposing that an object is in cubical shape and we need put into it a certain liquid. Then, we need to find out the number of volume of that particular water that can be put in that particular cube. To find out the number of litres that can be put in that particular cube-shaped object, we need to find out the volume of that particular cube-shaped object. And, this can be only attained by using the below-given formula:
Thus, the formula for calculating the volume of the cube will be derived as:
Volume of cube = a3, cubic units.
Related Videos:
- Surface area of cube
- Lateral surface area of cube
- Cuboid
- Volume of a cuboid
- Surface area of a cuboid
- Lateral surface area of a cuboid
Length of Diagonal of Cube
The length of the diagonal of a cube can be calculated in the following manner:
Supposing that the length of the side of the cube is represented by a;
Then, the length of the diagonal of the face of the cube will be derived using the formula, which is = √2 a.
And, on the other hand, the length of Diagonal of Cube = √3 a
Properties of a cube
Now, we will look at the properties if the cube, which literally distinguishes the cube from the variety of different shaped object and thereby form a basis for our complete understanding of how a cube looks like, what sets it apart from other different shaped objects and how we can differentiate the cube from other different shaped objects:
- All the faces of a cube are in a square shape.
- All faces of the cube will be having equal dimensions and thereby form unilaterally as a square with equal sides of the square.
- Similar to the square, the angles of the cube plane will have a right angle, thereby providing the cube with equal angles at the plane angles, which is the right angle (90 degrees).
- Although the cube has a total of six different faces, each and every face side of the cube meets the other four faces making the cube look like a square-shaped object.
Important Chapters:
Similar Questions
Knowledge Check
- Question 1 - Select One
Following frightening diagrams show identical cubes such that edge of cube 2 lies exactly in the middle of one of the faces of Cube 1 and Cube 4 has a corner at the body centre of the cube 3 . Find the contribution (in fraction) of the spheres shown to each of the cube 1 ,2 , 3 and 4 respectively is
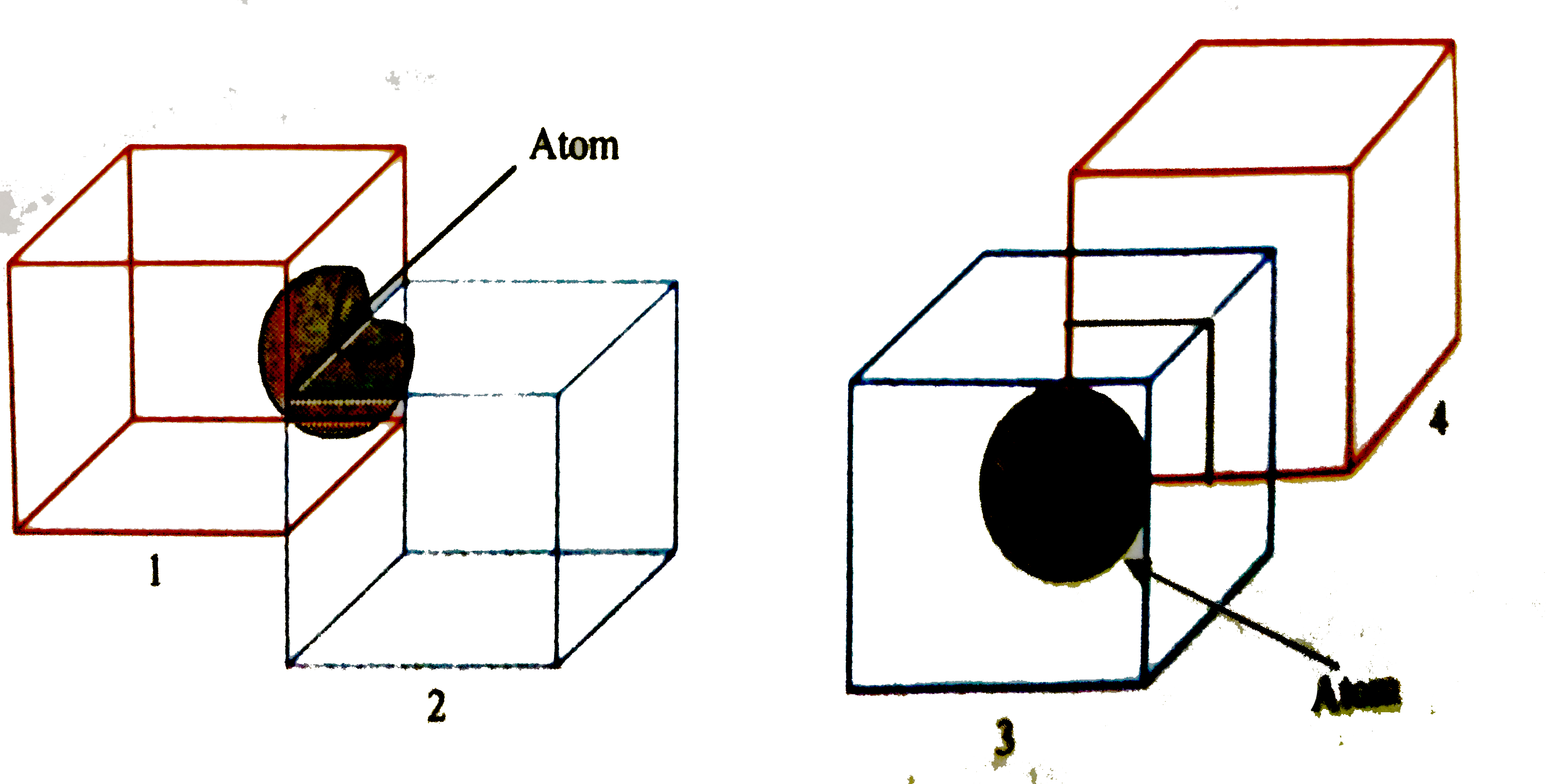 A12,14,1,18B12,14,18,1C18,14,1,12D18,14,12,1
A12,14,1,18B12,14,18,1C18,14,1,12D18,14,12,1 - Question 2 - Select One
Statements :
All spheres are cones
Some cubes are cones
All circles are cubes
Conclusions:
(i) No cube is sphere
(ii) All spheres may be cubes
(iii) Some cones are not circles
(iv) At least some cubes are circles
(v) Some cones which are cubes may be circlesA(i) & (ii) does not followB(i) & (iii) does not followC(ii)& (v) does not followD(iii) & (iv) does not follow


