Square
Step-by-Step Solution for Understanding Squares
1. Definition of a Square:
A square is a special type of quadrilateral where all four sides are equal in length and all four angles are equal to 90 degrees.
Hint: Remember that a square is a specific type of rectangle and rhombus.
2. Labeling the Square:
Let's label the vertices of the square as A, B, C, and D in a clockwise manner.
Hint: Visualizing the square and labeling the corners helps in understanding its properties better.
3. Properties of a Square:
- Equal Sides: All sides of the square are equal. If one side is of length 'A', then:
- AB = BC = CD = DA = A
- Equal Angles: All angles in a square are right angles (90 degrees).
- ∠A = ∠B = ∠C = ∠D = 90°
Hint: To remember the properties, think of a square as a perfect shape with symmetry.
4. Diagonals of the Square:
- Draw the diagonals AC and BD.
- The diagonals bisect each other at point O and are equal in length (D1 = D2).
- The diagonals intersect at right angles (90 degrees).
Hint: Diagonals in a square not only bisect each other but also create four right triangles.
5. Area of the Square:
- The area of a square can be calculated using the formula:
Area=side2=A2
- Alternatively, if we consider the square as composed of two triangles, we can calculate the area of each triangle:
- Area of triangle ABC = 12×base×height=12×A×A=A22
- Area of triangle ADC = 12×base×height=12×A×A=A22
- Therefore, the total area of the square is:
Area=A22+A22=A2
Hint: The area can be thought of as the total space enclosed within the square.
Summary
A square is a quadrilateral with equal sides and angles of 90 degrees. Its diagonals bisect each other at right angles and are equal in length. The area of a square is calculated using the formula A2, where A is the length of one side.
A square is a special type of quadrilateral where all four sides are equal in length and all four angles are equal to 90 degrees.
Let's label the vertices of the square as A, B, C, and D in a clockwise manner.
- Equal Sides: All sides of the square are equal. If one side is of length 'A', then:
- AB = BC = CD = DA = A
- Equal Angles: All angles in a square are right angles (90 degrees).
- ∠A = ∠B = ∠C = ∠D = 90°
- Draw the diagonals AC and BD.
- The diagonals bisect each other at point O and are equal in length (D1 = D2).
- The diagonals intersect at right angles (90 degrees).
- The area of a square can be calculated using the formula:
Area=side2=A2
- Alternatively, if we consider the square as composed of two triangles, we can calculate the area of each triangle:
- Area of triangle ABC = 12×base×height=12×A×A=A22
- Area of triangle ADC = 12×base×height=12×A×A=A22
- Therefore, the total area of the square is:
Area=A22+A22=A2
A square is a quadrilateral with equal sides and angles of 90 degrees. Its diagonals bisect each other at right angles and are equal in length. The area of a square is calculated using the formula A2, where A is the length of one side.
Similar Questions
In figure XY∣∣ seg AC. If 2AX=3BX and XY=9, complete the activity to find the value of AC.
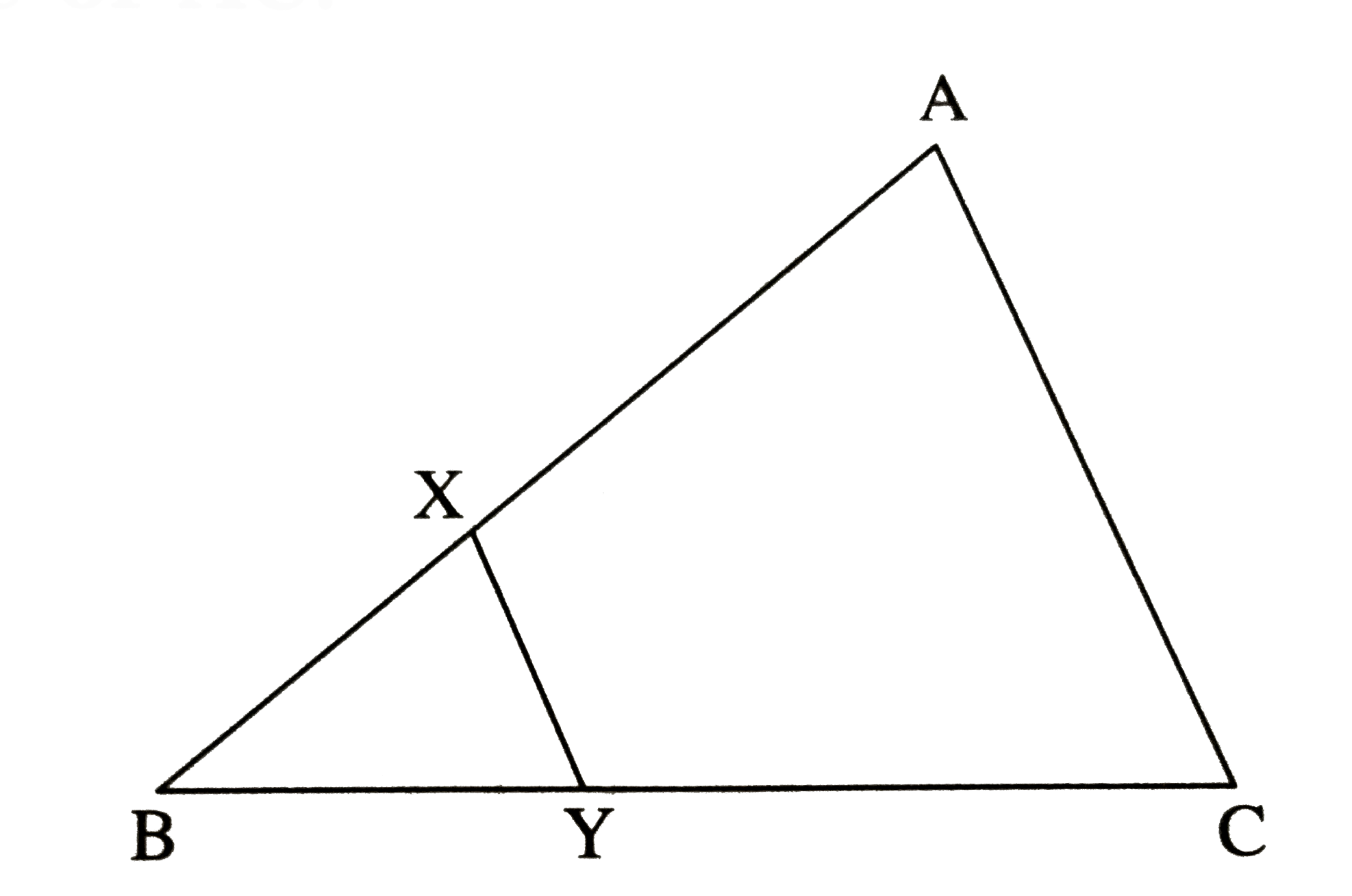
Activity: 2AX=3BX
∴AXBX=□□
∴AX+BXBX=□+□□.........(By componendo)
∴ABBX=□□.............1
ΔBCA~ΔBYX.......(□ test of similarity)
∴BABX=ACXY
..............(Corresponding sides of similar triangles)
∴□□=AC9
∴AC=□ ...........[From 1]View SolutionA circle, a square and an equilateral triangle have the same area. The correct increasing order of the perimeters will be (a) triangle, square, circle (b) triangle, circle, square (c) circle, triangle, square (d) circle, square, triangle
View Solution
Knowledge Check
- Question 1 - Select One
A square is drawn by joining mid pint of the sides of a square. Another square is drawn inside the second square in the same way and the process is continued in definitely. If the side of the first square is 16 cm, then what is the sum of the areas of all the squares ?
A256 sq cmB512 sq cmC1024 sq cmD512/3 sq cm - Question 2 - Select One
A square is drawn by joining mid-points of the sides of a square. Another square is drawn inside the second square in the same way and the process is continued indefinitely. If the side of the first square is 16 cm, then what is the sum of the areas of all the squares ?
(a)256sq. Cm
(b)512 sq. cm
(c)1024sq. Cm
(d)512/3sq. CmA256sq. CmB512 sq. cmC1024sq. CmD512/3sq. Cm - Question 3 - Select One
The length of side of a square is 'a' metre. A second square is formed by joining the middle points of this square. Then a third square is formed by joining the middle points of the sides of the second square and so on. Then, the sum of the areas of squares which carried upto infinity, is
Aa2B2a2C3a2D4a2
A side of a square is 16 cm. A new square is formed by joining the midpoints of sides, again a new square is formed by joining the mid-points of the new square and this process goes on till infiity. Find the total area of such square formed ?
View SolutionIn the figure shown square II is formed by joining the mid-points of square II
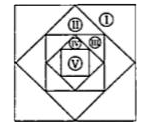
and so on . In this way total five squares are drawn . The sides of the square I is 'a' cm.
What is the total area of all the five squares ?View Solution

