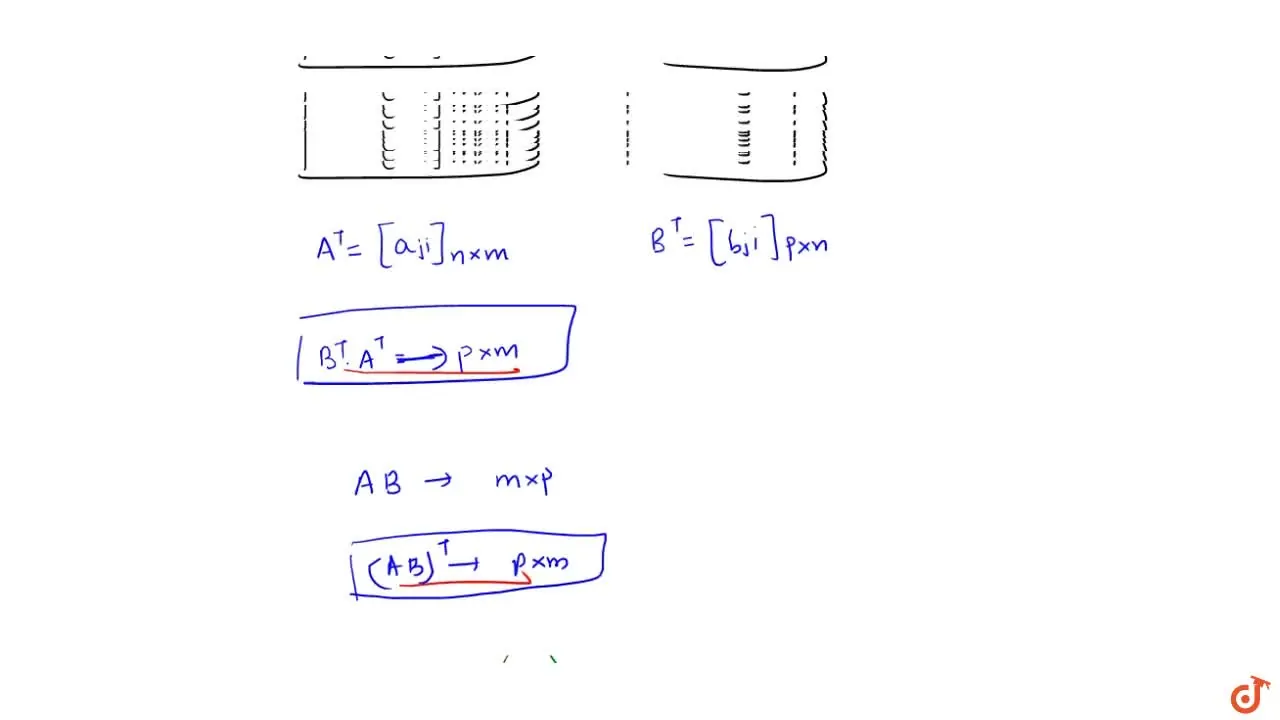
If A and B are two matrices such that AB is defined; then ${(A B)}^{T} = B^{T} . A^{T}$

Video Solution

Answer

Step by step video & image solution for If A and B are two matrices such that AB is defined; then (AB)^T = B^T . A^T by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS MATRICES

Knowledge Check

If A and B are two matrices such that $A B = B and B A = A$ then $A^{2} + B^{2} =$ (A) 2AB (B) 2BA (C) A+B (D) AB
A $A^{2} + B^{2}$
B $O$
C $A^{2} + 2 A B + B^{2}$
D $A + B$

If A and B are two matrices such that Aand AB are both defined, then
View Solution
If A and B are two matrices such that A+B and AB are both defined, then
View Solution
If A and B are two matrices such that A+B and AB are both defined, then
View Solution
If A and B are two matrices such that A+B and AB are both defind, then
View Solution
If A and B are two matrices such that AB=B and BA=A , then $A^{2} + B^{2} =$
View Solution
If A and B are two matrices such that $A + B$ and AB are both defined, then
View Solution
If A and B are two matrices such that $A B = B and B A = A$ then $A^{2} + B^{2} =$ (A) 2AB (B) 2BA (C) A+B (D) AB
View Solution

If A and B are two matrices such that AB is defined; then ${(A B)}^{T} = B^{T} . A^{T}$

Similar Questions

Knowledge Check

If A and B are two matrices such that $A B = B and B A = A$ then $A^{2} + B^{2} =$ (A) 2AB (B) 2BA (C) A+B (D) AB

Recommended Questions

If A and B are two matrices such that AB is defined; then (AB)T=BT.AT

Similar Questions

Knowledge Check

If A and B are two matrices such that AB=BandBA=A then A2+B2= (A) 2AB (B) 2BA (C) A+B (D) AB

Recommended Questions

If A and B are two matrices such that AB is defined; then ${(A B)}^{T} = B^{T} . A^{T}$

If A and B are two matrices such that $A B = B and B A = A$ then $A^{2} + B^{2} =$ (A) 2AB (B) 2BA (C) A+B (D) AB