Question

Addition Modulo

Explanation

What is Addition Modulo?

Here, we will learn about the addition property of modular arithmetic:

(A + B) mod C = (A mod C + B mod C) mod C

Example:

Let A=14, B=17, C=5

Let's verify: (A + B) mod C = (A mod C + B mod C) mod C

LHS = Left Hand Side of the Equation

RHS = Right Hand Side of the Equation

LHS = (A + B) mod C

LHS = (14 + 17) mod 5

LHS = 31 mod 5

LHS = 1

RHS = (A mod C + B mod C) mod C

RHS = (14 mod 5 + 17 mod 5) mod 5

RHS = (4 + 2) mod 5

RHS = 1

LHS = RHS = 1

Intuition Behind Modular Addition

Observe the figure below. If we want to calculate 12+9 mod 7 we can easily go around the modular circle for a sequence of 12+9 steps clockwise (as shown in the bottom left circle).

   

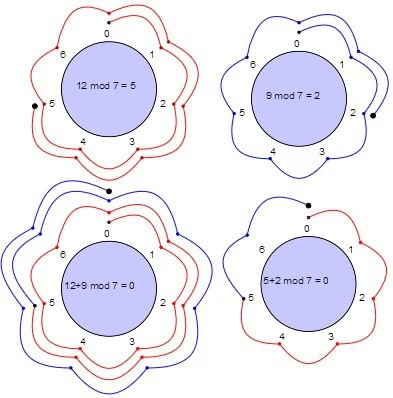
We can take a shortcut by observing that every 7 steps we end up in the same position on the modular circle. These complete loops around the modular circle don’t contribute to our final position. We ignore these complete loops around the circle by calculating each number mod 7 (as shown in the two upper modular circles). This will give us the number of clockwise steps, relative to 0, that contributed to each of their final positions around the modular circle.

Now, we only have to go around the circle clockwise the total of the number of steps that contributed to each of numbers final position (as shown in the bottom right modular circle). This method applies, in general, to any two integers and any modular circle.

Proof for Modular Addition

We will prove that (A + B) mod C = (A mod C + B mod C) mod C

We must show that LHS=RHS

From the quotient remainder theorem we can write A and B as:

A = C * Q1 + R1 where 0 ≤ R1 < C and Q1 is some integer. A mod C = R1

B = C * Q2 + R2 where 0 ≤ R2 < C and Q2 is some integer. B mod C = R2

(A + B) = C * (Q1 + Q2) + R1+R2

LHS = (A + B) mod C

LHS = (C * (Q1 + Q2) + R1+ R2) mod C

We can eliminate the multiples of C when we take the mod C

LHS = (R1 + R2) mod C

RHS = (A mod C + B mod C) mod C

RHS = (R1 + R2) mod C

LHS=RHS= (R1 + R2) mod C