Question

Domain and range of a relation

Explanation

What is Domain and range of a relation?

The nature of relationship often limits the domain and range of a function.  For example, you toss a ball into the air and consider the occurrence of the function of time and height when you catch it. Here input is the time where output is the height. Every value of time is the domain during the throw where it gets counted instantly when the ball leaves your hand till it returns. If we assume that the ball was in the air for 8 seconds, then the domain would be 0-8 seconds

On the other hand, the height of the ball when it was thrown is the range.  If your hand was 4 feet above the ground while throwing and catching the ball and the height it flew was 14 feet off the ground then we can say that the range is 4-14 feet.  This is because of the reason that during this interval, height changes continuously. So, it is not possible to write down every possible output where the starting and stopping values can be noted.

In domain and range of a relation, if we taken R to be a relation from set A to set B, then:

• The domain of R indicates the set of all first components of the ordered pairs that belongs to R.

             So, Dom(R) = {a ∈ A: (a, b) ∈ R for some b ∈ B}.

• The set of all second components of the ordered pairs belonging to R is called the range of R is defined by the set of all second components  that belongs to R of the ordered pairs

Therefore, range of R = {b ∈ B: (a, b) ∈ R for some a ∈ A}.

           In this case, Domain (R) = {a : (a, b) ∈ R} and Range (R) = {b : (a, b) ∈ R}

Examples on domain and range of a relation

1. In the given ordered pair (4, 6); (8, 4); (4, 4); (9, 11); (6, 3); (3, 0); (2, 3) find the following relations. Also, find the domain and range.



(a) Is two less than

(b) Is less than

(c) Is greater than

(d) Is equal to



Solution:



(a) R₁ is the set of all ordered pairs whose 1^st component is two less than the 2^nd component.

Therefore, R₁ = {(4, 6); (9, 11)}

Also, Domain (R₁) =  all first components of the set R₁ = {4, 9} and Range (R₂) = all second components of the set R₂ = {6, 11}

(b) R₂ is the set of all ordered pairs whose 1 ^st component is less than the second component.

Therefore, R₂ = {(4, 6); (9, 11); (2, 3)}.

Also, here, Domain (R₂) = {4, 9, 2} whereas Range (R₂) = {6, 11, 3}

(c) R₃ is the set of all ordered pairs whose 1 ^st component is greater than the second component.

Therefore, R₃ = {(8, 4); (6, 3); (3, 0)}

Also, here, Domain (R₃) = {8, 6, 3} whereas Range (R₃) = {4, 3, 0}

(d) R₄ is the set of all ordered pairs whose 1 ^st component is equal to the second component.

Therefore, R₄ = {(3, 3)}

Also, here, Domain (R) = {3} whereas Range (R) = {3}



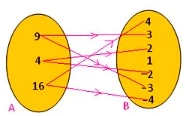
2. Let A = {2, 3, 4, 5} and B = {8, 9, 10, 11}.

Let relation ‘is factor of’ from A to B be ‘R’



(a) Write R in the roster form. Also, find Domain and Range of R.



(b) Represent the relation by drawing an arrow diagram.



Solution:



(a) Clearly, R includes elements (a, b) where a happens to be a factor of b.



Therefore, Relation (R) in the roster form is R = {(2, 8); (2, 10); (3, 9); (4, 8), (5, 10)}



Thus, Domain (R) = Set of all first components of R = {2, 3, 4, 5} and Range (R) = Set of all second components of R = {8, 10, 9}

(b) Below is the arrow diagram representing R:

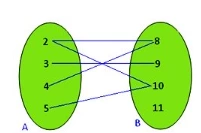
3. The arrow diagram below shows the relation (R) from set A to set B. Write this relation in the roster form.

 

Solution:



Here, R consists of elements (a, b), such that ‘a’ is square of ‘b’

i.e., a = b².



Therefore, in roster form R = {(9, 3); (9, -3); (4, 2); (4, -2); (16, 4); (16, -4)}

Let A = {1, 2, 3, 4, 5} and B = {p, q, r, s}. Let R be a relation from A in B defined by

R = {1, p}, (1, r), (3, p), (4, q), (5, s), (3, p)}

Find domain and range of R.



Solution:

Given R = {(1, p), (1, r), (4, q), (5, s)}

Domain of R = set of all elements of R of the first components = {1, 3, 4, 5}

Range of R = set of all elements of R of the second components = {p, r, q, s}