A block of mass m is placed inside a smooth hollow cylinder of radius R kept horizontally. Initially system was at rest. Now cylinder is given constant acceleration 2g in the horizontal direction by external agent. Find the maximum angular displacement of the block with the vertical.
 .
.
The correct Answer is:2tan−1(2).
Free body diagram is :
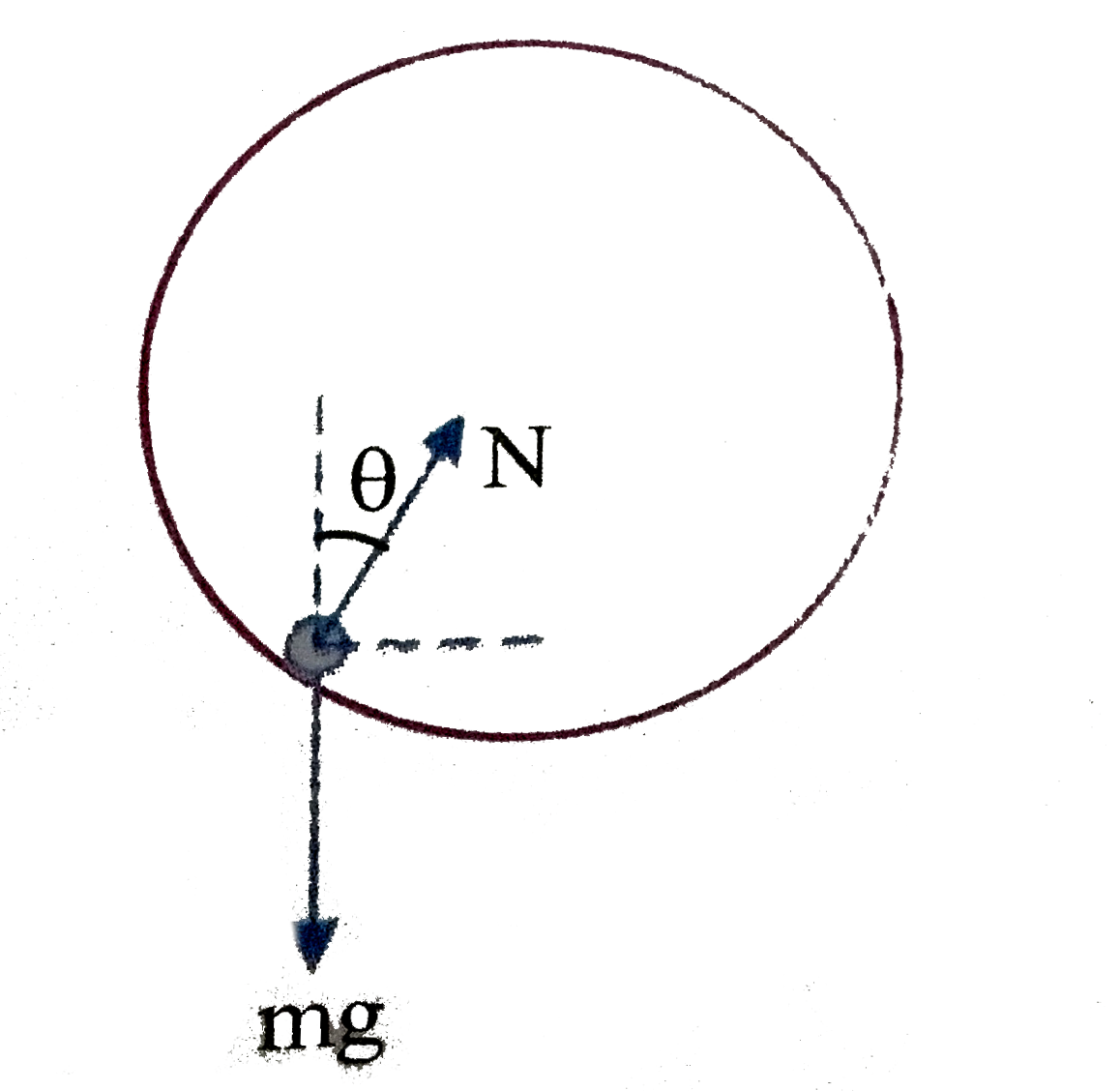
Ncosθ=mg
Nsinθ=m(2g)
⇒tanθ=2
⇒θ=tan−1(2)
∴ Maximum possible angular dispalcement
=2θ
=2tan−1(2).
Topper's Solved these Questions
Similar Questions
A block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionA block of mass m is placed at the bottom of a massless smooth wedge which if placed on a horizontal surface. When we push the wedge with a constant force, the block moves up the wedge. Find the work done by the external agent when the block has a speed v and is reaches the top of the wedge.

View Solution
Knowledge Check
A small sphere of mass m and radius r is placed inside a horizontal hollow cylinder of radius R. Now cylinder rotating with some angular acceleration which slowly increases from zero to certain value α.
 AMaximum angle θ formed by line joining centre will be θ=sin−1(2αR5g)BAngular velocity of sphere will be ω′=ωrR where ω is angular velocity of cylinderCSphere will keep rotating at lowest positionDK.E. of sphere becomes constant when it reaches maximum height
AMaximum angle θ formed by line joining centre will be θ=sin−1(2αR5g)BAngular velocity of sphere will be ω′=ωrR where ω is angular velocity of cylinderCSphere will keep rotating at lowest positionDK.E. of sphere becomes constant when it reaches maximum heightA block of mass m is kept on an inclined plane of mass 2m and inclination α to horizontal. If the whole system is accelerated such that the block does not slip on the wedge then :
AThe normal reaction acting on 2m due to m is mgsecθBFor the block m to remain at rest with respect to wedge a force F=3mgtanα must be applied on 2mCThe normal reaction acting on 2m due to m is mgsecθDPseudo force acting on m with respect to ground is mgtanα towards west.A block of mass m is placed in equilibrium on a moving plank. The maximum horizontal acceleration of the plank for μ=0.2 is:
A2m/s2B3m/s2Cdependent on the mass mDnone of these
A block of mass m is placed on a smooth slope of angle θ.The whole system (slope + block) is moved horizontally with acceleration a in such way that the block does not slip on the slope.Hence a = ________.
View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionA block of mass m is placed on a smooth wedge of inclination θ. The while system is acceleration horizontally so that the block does not slip. Find (a) horizontal acceleration, (b) normal force between the block and the wedge and (c) the horizontal force applied on the wedge.
View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force of the block of mass M.
View SolutionA block of mass m is placed on a smooth wedge of wedge angle θ The whole system is accelerated horizontally so that the block does not slip on the wedge. The force (normal reaction) exerted by the wedge on the block has a magnitude:
View Solution