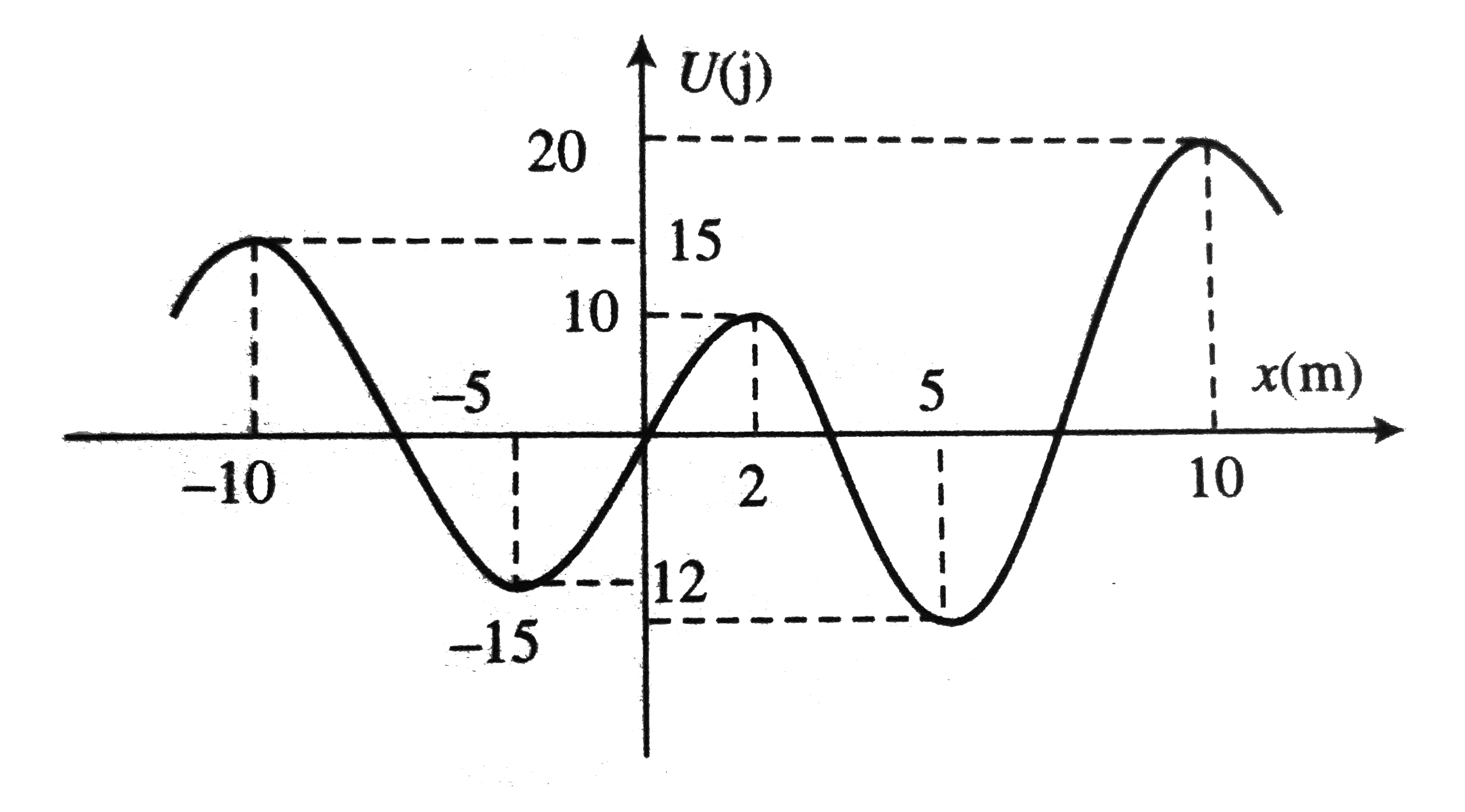
In the figure the variation of potential energy of a particle of mass m=2kg is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis.
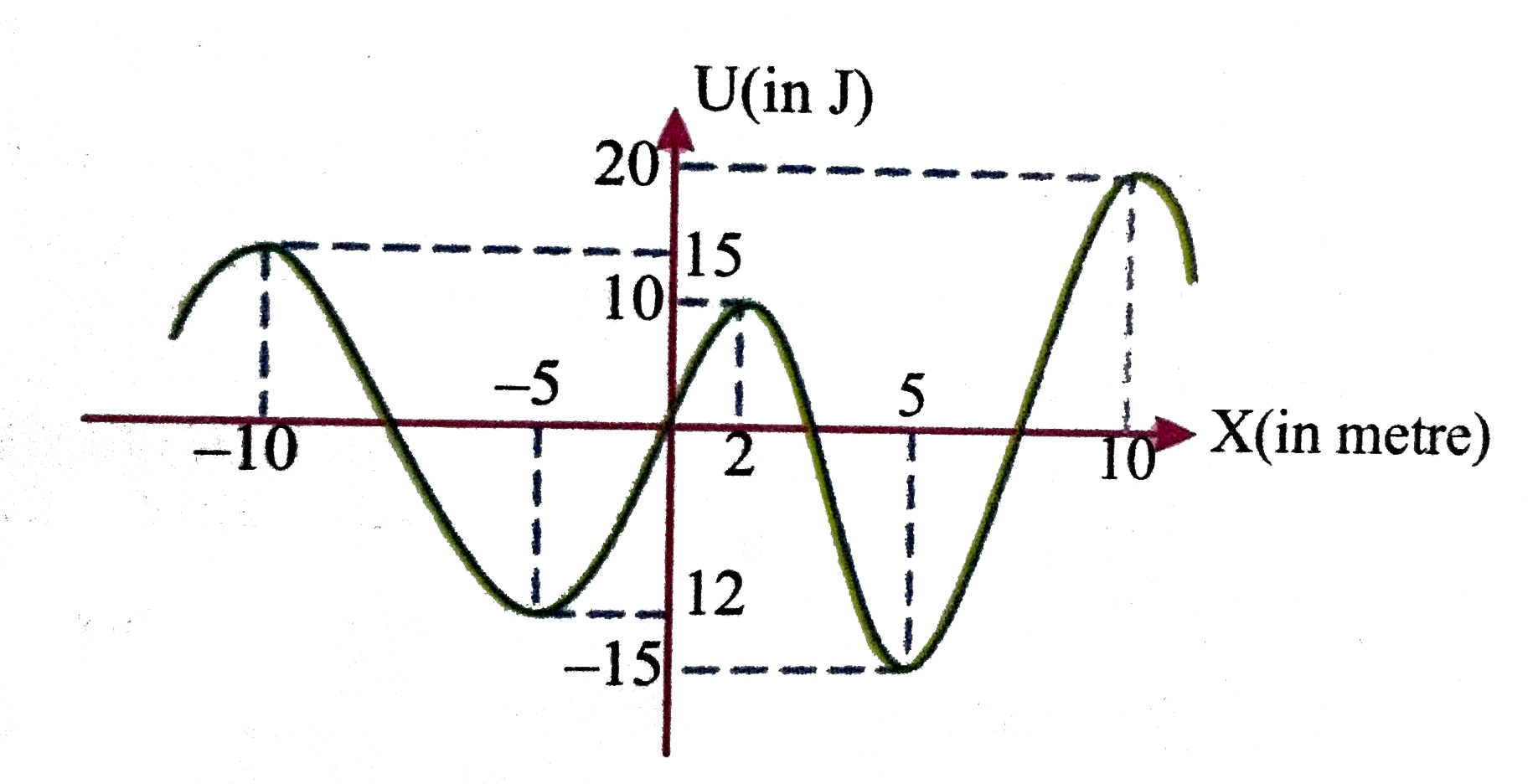
x=−5m and x=10m position of the particle are respectively of
neutral and stable equilibrium.
neutral and unstable equilibrium.
unstable and stable equilibrium.
stable and unstable equilibrium.
The correct Answer is:D
Step by step video, text & image solution for In the figure the variation of potential energy of a particle of mass m = 2kg is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis. x = - 5m and x = 10 m position of the particle are respectively of by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-VI (Integer)
Explore 12 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-VI (Multiple Answer)
Explore 11 Videos
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE IV
Explore 43 Videos
Similar Questions
The potential energy of a particle under a conservative force is given by U(x)=(x2−3x) J. The equilibrium position of the particle is at
View SolutionWhat is the gravitational potential energy of a particle of mass m kept at a distance x from the centre of a disc of mass M on its axis ? The radius of the disc is R.
View Solution
Knowledge Check
In the figure the variation of potential energy of a particle of mass m=2kg is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis.
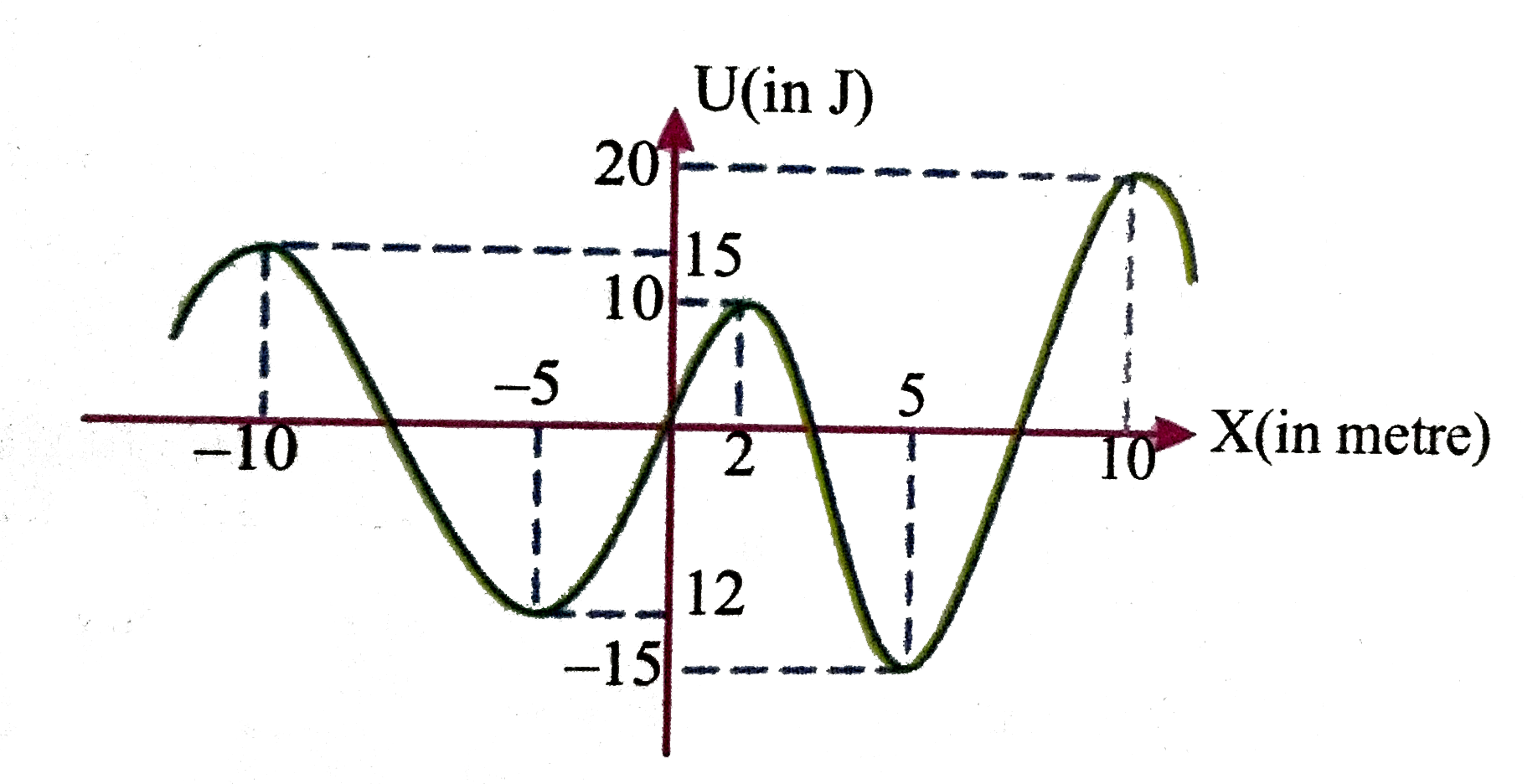
If the particle is released at the origin thenAit will move towards positive x-axis.Bit will move towards negative x-axis.Cit will remain stationary at the origin.Dits subsequent motion cannot be decided due to lack of information.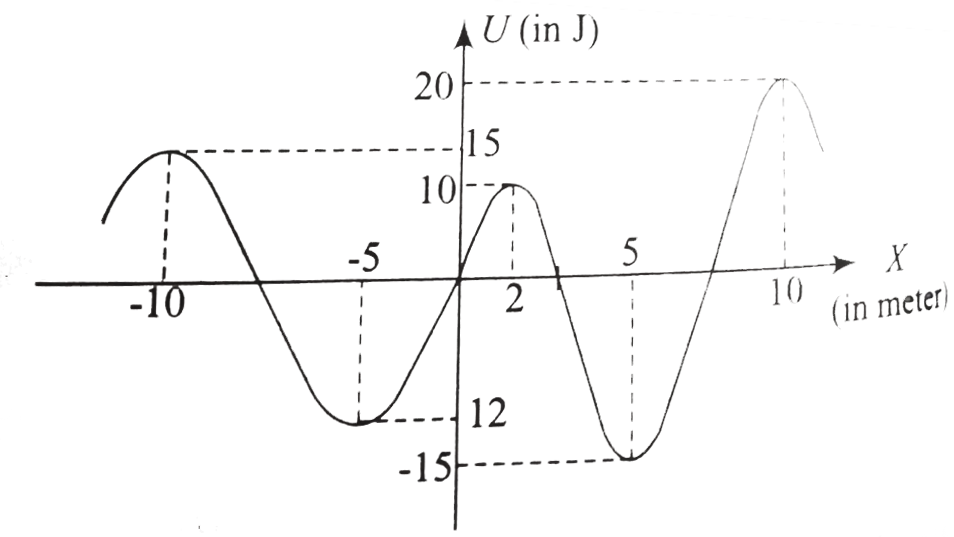
In the figure the variation of potential energy of a particle of mass m=2kg is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis. Which of the following statements are correct about the particle:AIf it is released at the origin it will move in negative x-axisBIf it is released at x=2+△ where △→0 then its maximum speed will be 5ms and it will perform oscillatory motionCIf initially x=−10m and →u=√6ˆims then it will cross x=10mDx=−5m and x=+5 m are unstable equilibrium positions of the particle.In the figure, the variation of potential energy of a particle of mass m = 2kg is represented with respect to its x-coordinate. The particle moves under the effect of this conservative force along the X-axis.
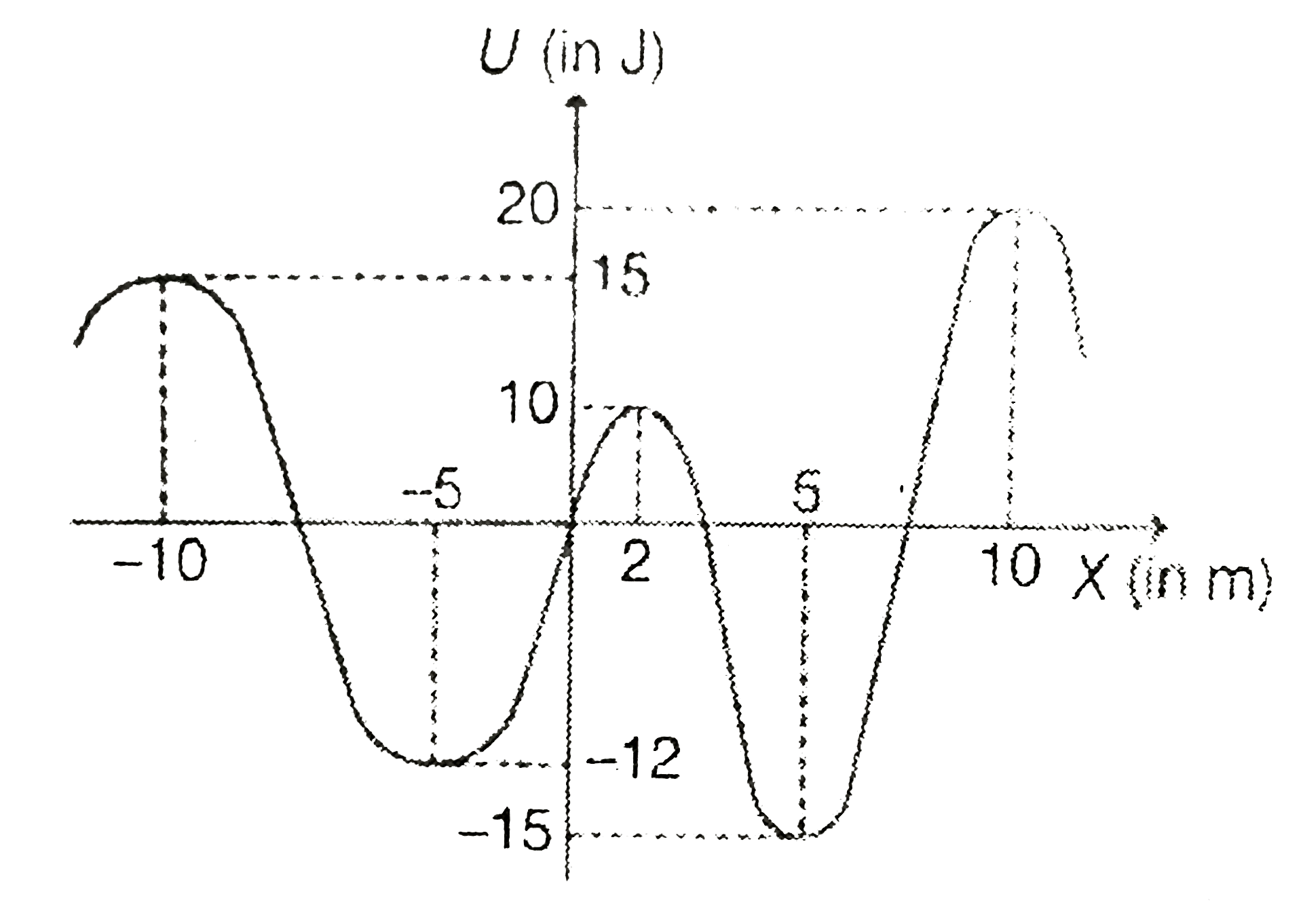
If the particle is released at the origin, thenAit will move towards positive x-axisBit will move towards negative x-axisCit will remain stationary at the originDEither of (a) or (b)
In figure, the variation of potential energy of a particle of mass m=2kg is represented w.r.t its x-coordinate. The particle moves under the effect of the conservative force along the x-axis. Which of the following statements is incorrect about the particle?
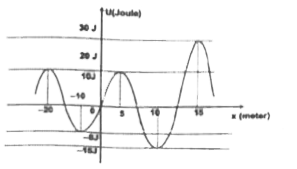
View SolutionThe variation of potential energy of a particle of mass m = 5kg to its x-coordinate . The particle moves under the effect of this conservative force only along the x-axis. Then, choose the correct option.
View SolutionIn the figure, the variation of potential energy of a particle of mass m = 2kg is represented with respect to its x-coordinate. The particle moves under the effect of this conservative force along the X-axis.
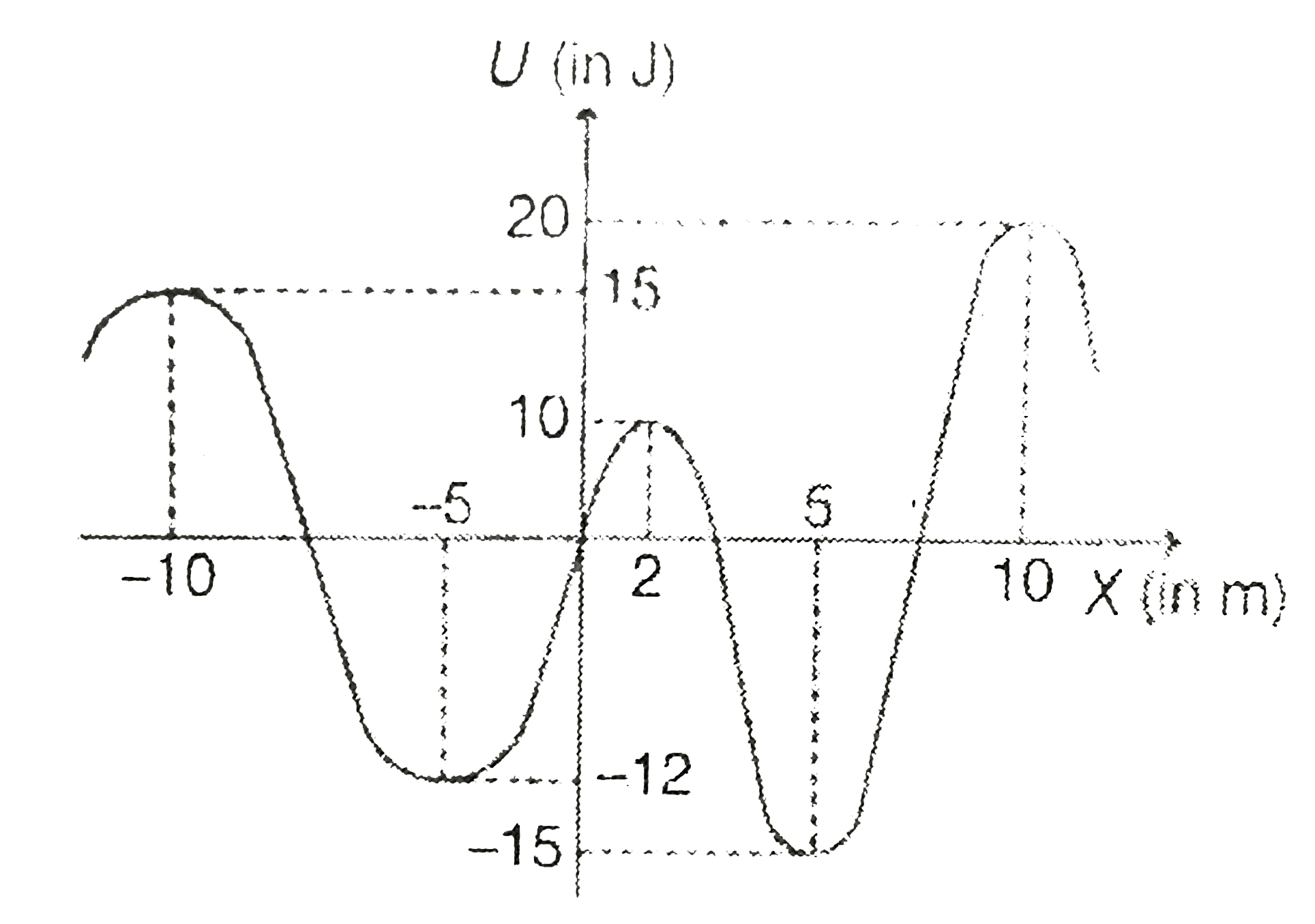
If the particle is released at x=2+Δ where Δ→0 (it is positive), then its maximum speed in subsequent motion will be
View SolutionThe potential energy of a particle moving along x-axis is given by U=20+5sin(4πx), where U is in J and x is in metre under the action of conservative force :
View Solutionvx is the velocity of a particle moving along the x-axis as shown in the figure. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s ?
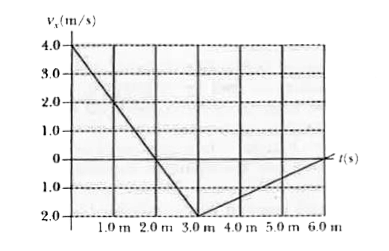
View Solution

