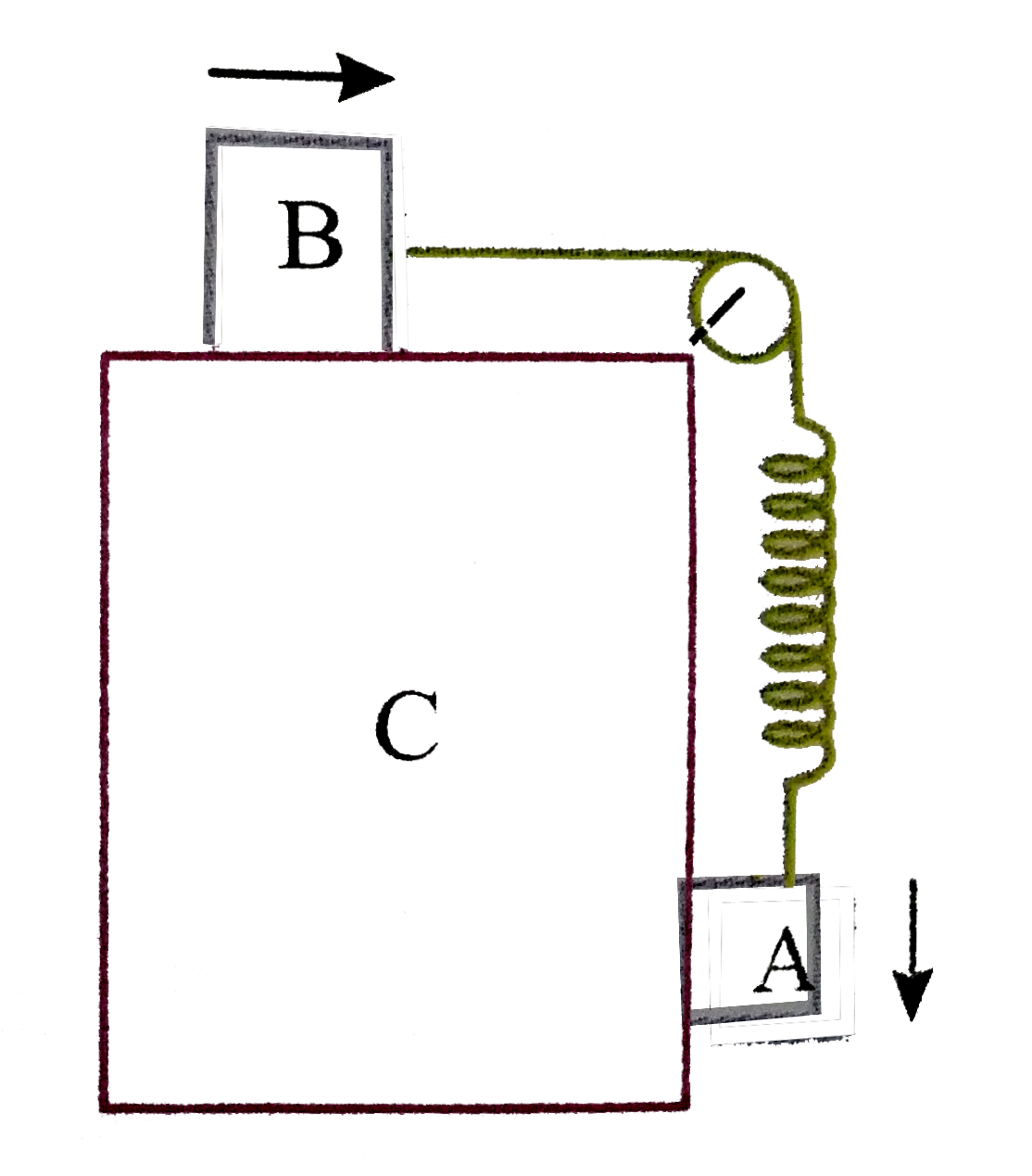
Two blocks A and B are connected to each other by a string and a spring , the string passes over a frictionless pulley as shown in the figure. Block B slides over the horizontal top surface of a stationary block C and the block A slides along the vertical side of C, both with the same uniform speed. The coefficient of friction between the surface and blocks is 0.5K=2000N/m. If mass of A is 2kg calculate mass of B.
 .
.
The correct Answer is:4
Normal reaction between blocks A and C will be zero. Therefore, there will be no friction between them. Both A and B are moving with uniform speed. Therefore, net force on them should be zero For equilibrium of A:mAg=kx
∴x=mAgk=(2)(10)2000=0.01m
For equilibrium of B , μmBg=T=kx=mAg
∴mB=mAμ=20.5=4kg.
 .
.
Topper's Solved these Questions
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-VI (Single Answer)
Explore 31 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-VI (Multiple Answer)
Explore 11 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-V (Comprehension)
Explore 22 Videos
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE IV
Explore 43 Videos
Similar Questions
Two blocks A and B are connected to each other by a string and a spring, the string passes over a frictionless pulley as shown in Block B slides over the horizontal surface of a stationary block C and the block. A slides along the vertical side of C, both with same uniform speed. The coefficient of friction between the surface of the blocks is 0.2 Force constant of the spring is 1960 N/m if the mass of block A is 2 kg calculate the mass of the block B and the energy stored in the spring.
View SolutionTwo blocksA andB are connected to each other by a string and a spring , the spring pases and a frictionlesss pulley as down over in the figure . Block B sides over the horizental top surface of a strionry block C both with the verical side of C , both with the same conform speed
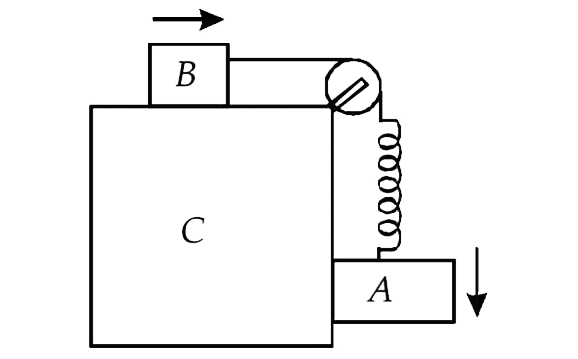
The coefficient of friction between the surface the of block is 0.2 force constant of the spring is 1960 newtons , if mass of block A is 2 kg , celculate the mass of block F and B and the energy stored is the spring
View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2Two blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is
 A4m/s2B2m/s2CzeroD6m/s2
A4m/s2B2m/s2CzeroD6m/s2Two blocks A and B , each of mass 10kg , are connected by a light string passing over a smooth pulley as shown in the figure. Block A will remain at rest if the friction on it is
 A50N up the planeB50N down the planeC100N up the planeD100N down the plane
A50N up the planeB50N down the planeC100N up the planeD100N down the plane
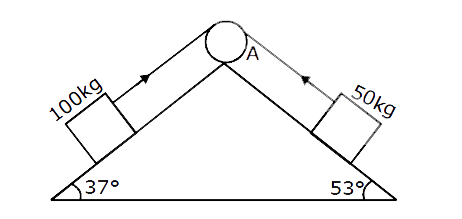
Two blocks are connected by a cord passing over a small frictionless pulley and resting on frictionless planes as shown in the figure. The acceleration of the blocks is :
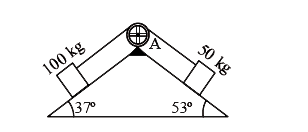
View SolutionTwo blocks are connected by a cord passing over a small frictionless pulley and resting on frictionless planes as shown in the figure The accleration of the blocks is-
View SolutionTwo blocks, each having mass m, are connected with an ideal string through ideal pulleys on a frictionless fixed wedge as shown in the figure. The acceleration of the blocks is
View SolutionBlock A of mass M in the system shown in the figure slides down the incline at a constant speed. The coefficient of friction between block A and the surface is 1 3 3 . The mass of block B is-

View SolutionTwo blocks A and B are connected by a light inextensible string passing over a fixed smooth pulley as shown in figure The coefficient of friction between the block A and B the horizontal table is μ=0.5. If the block A is just , find ratio of the masses of the blocks
View Solution

