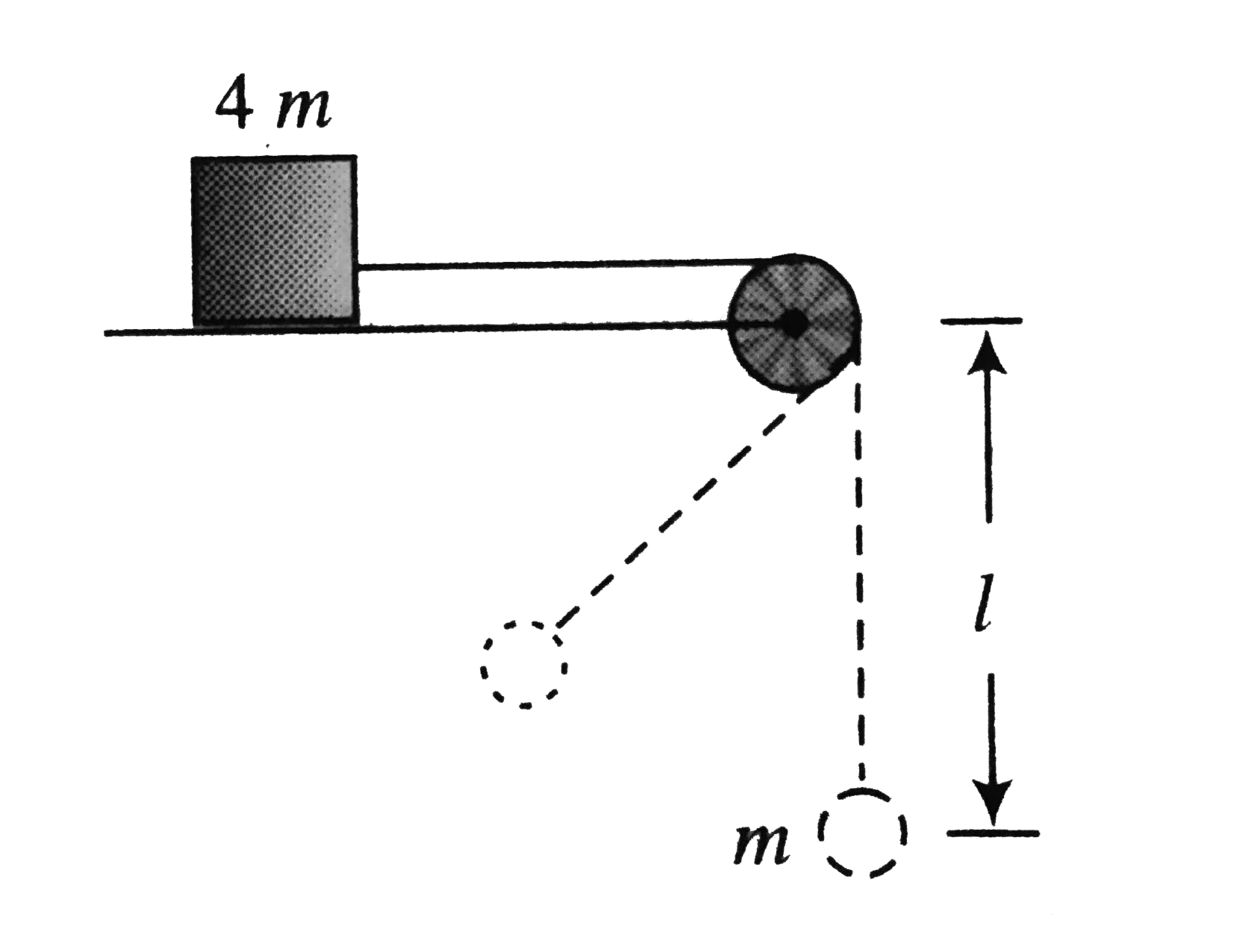
In the system shown in the figure the mass moves in a circular arc of angular amplitude . Mass is stationary. Then :
 .
.
the minimum value of coefficient of friction between the same of mass and the surface of the table is
the work done by gravitational force in the block is positive when it moves from to
the power delovered by the tension when moves from to is zero
The kinetic energy of in position equals the work done by gravitational force on the block when its from position to .
The correct Answer is:A, B, C, D
Step by step video, text & image solution for In the system shown in the figure the mass m moves in a circular arc of angular amplitude 60^@. Mass 4 m is stationary. Then : . by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-V (Comprehension)
Explore 22 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-V (Integer)
Explore 5 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-V (Single Answer)
Explore 24 Videos
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE IV
Explore 43 Videos
Similar Questions
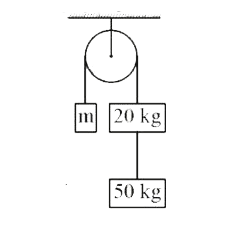
Find the mass m in the figure for the system to be at rest
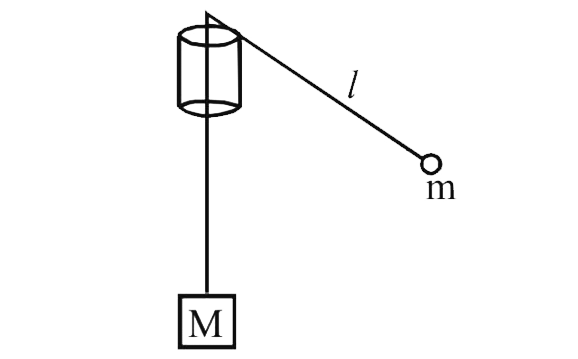
View SolutionA large mass M and a small mass m hang at two ends of a string that passes over a smooth tube as shown in the figure. The mass m moves around a circular path which lies in a horizontal plane. The length of string from the mass m to the top of the tube is l and θ is the 'angle' this length makes with the vertical. What should be the frequency of rotation of mass m, so that the mass M remains stationary?
View Solution
Knowledge Check
A body of mass m moves in a circular path with uniform angular velocity. The motion of the body has constant
AAccelerationBVelocityCMomentumDKinetic energyThe mass M shown in the figure oscillates in simple harmnonic motion and amplitude A. The amplitude of the point P is
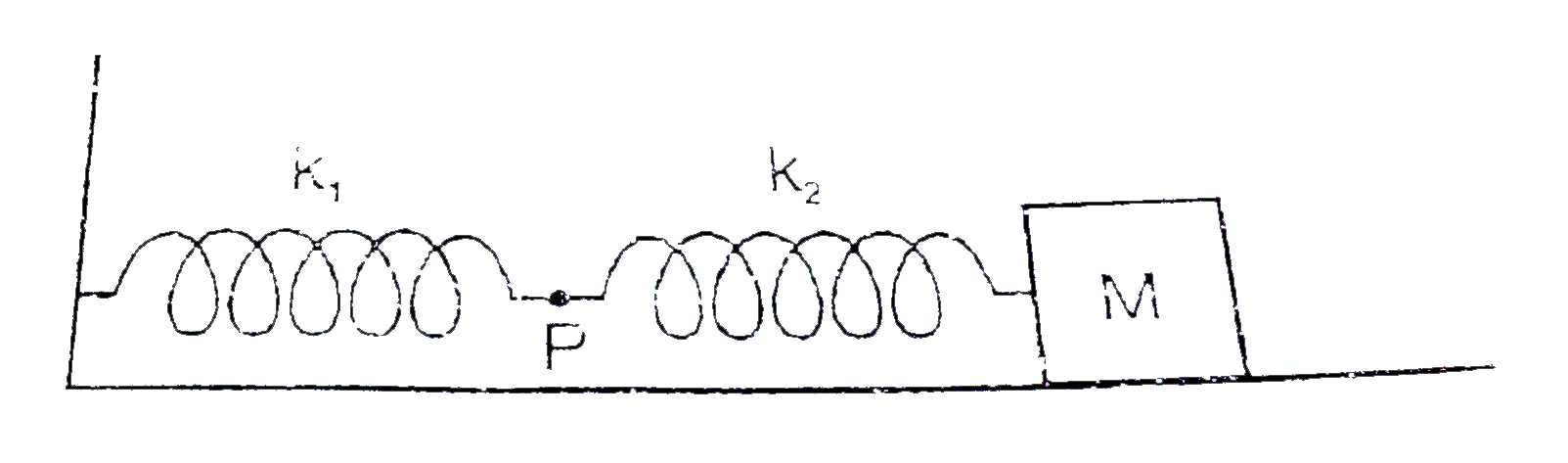 Ak1Ak2Bk2Ak1Ck1Ak1+k2Dk2Ak1+k2
Ak1Ak2Bk2Ak1Ck1Ak1+k2Dk2Ak1+k2A mass M is attached to a horizontal spring of force constant k fixed one side to a rigid support as shown in figure. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass M is in equilibrium position, another mass m is gently placed on it. When will be the new amplitude of ocillation?
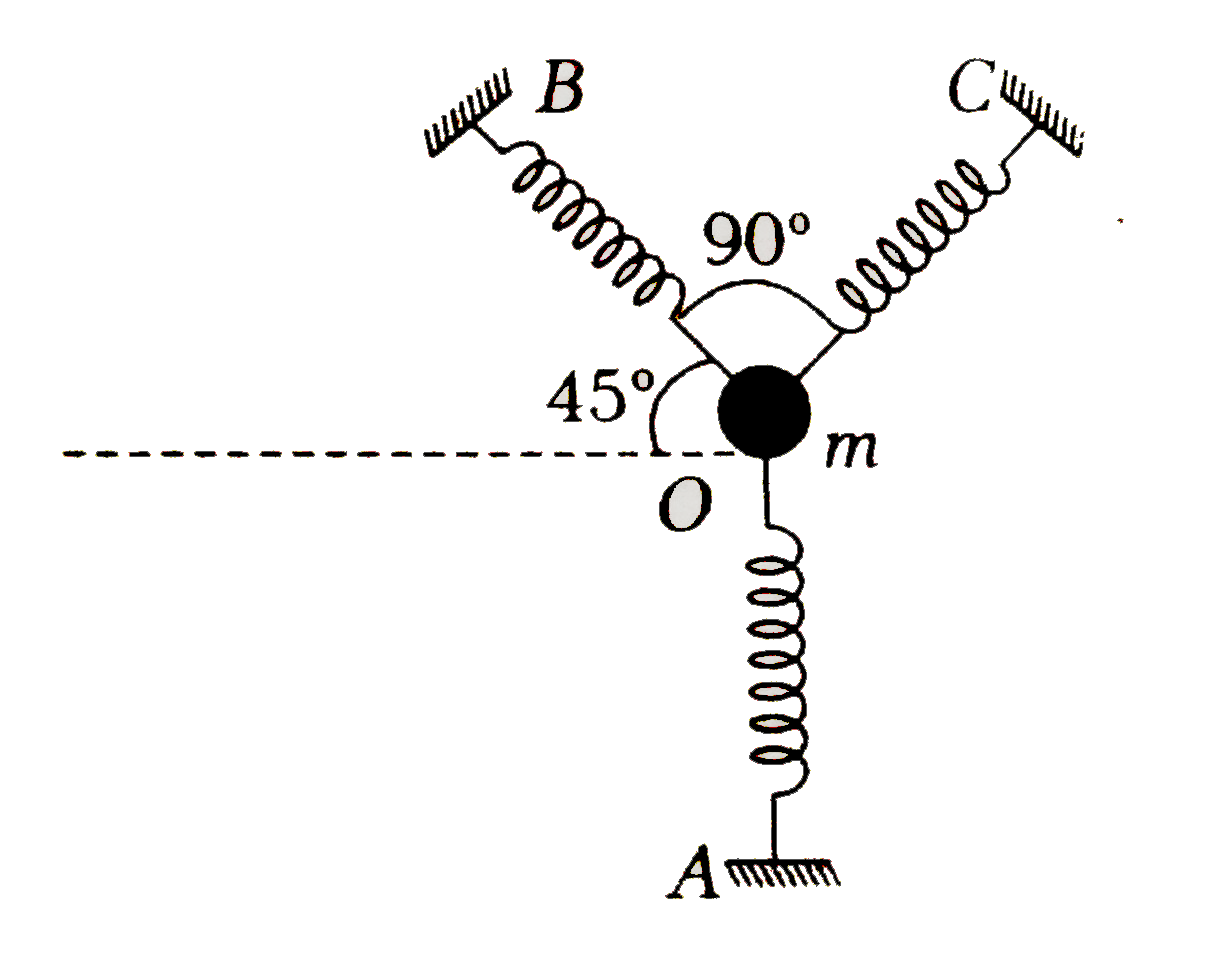
 A√(M+m)MAB√(M−m)MAC√M(M+m)AD√M(M−m)A
A√(M+m)MAB√(M−m)MAC√M(M+m)AD√M(M−m)A
For the equilibrium of the system shown, the value of mass m should be
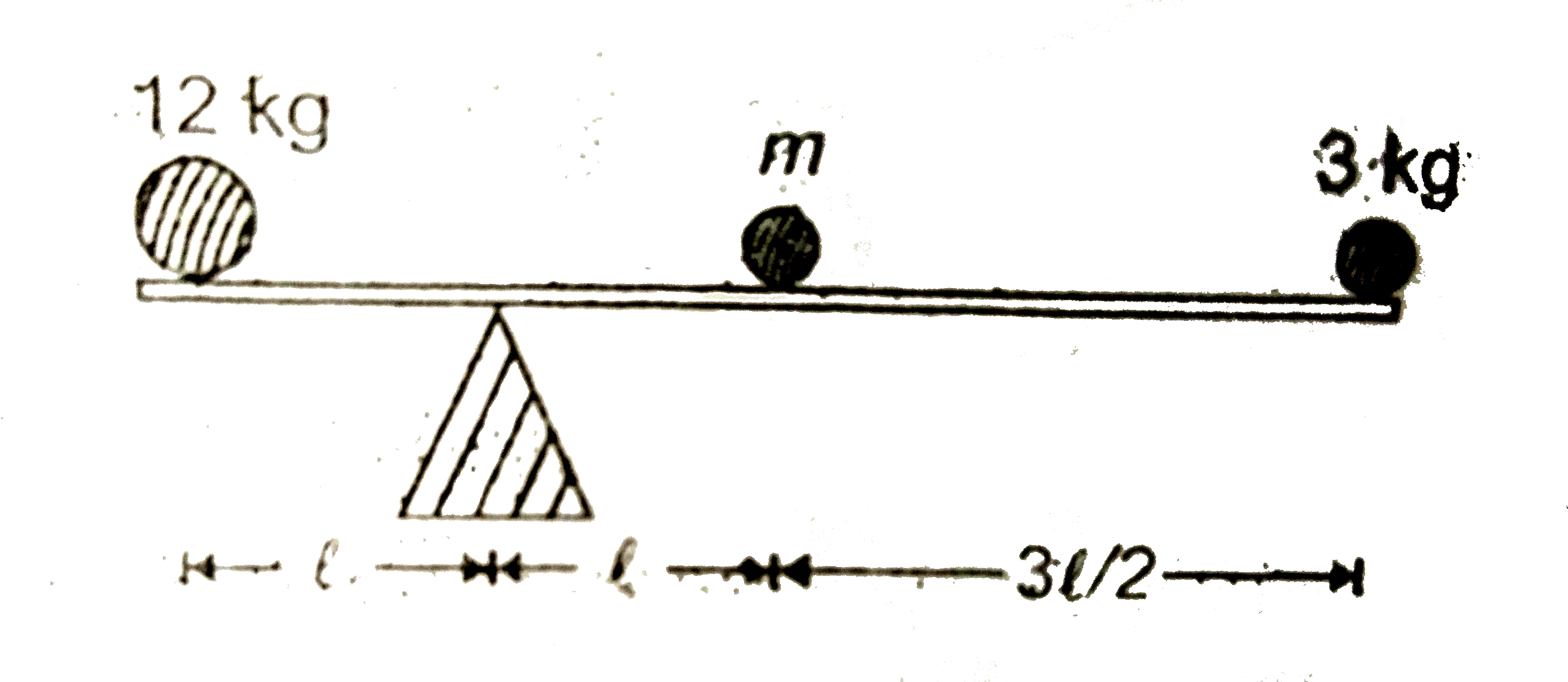
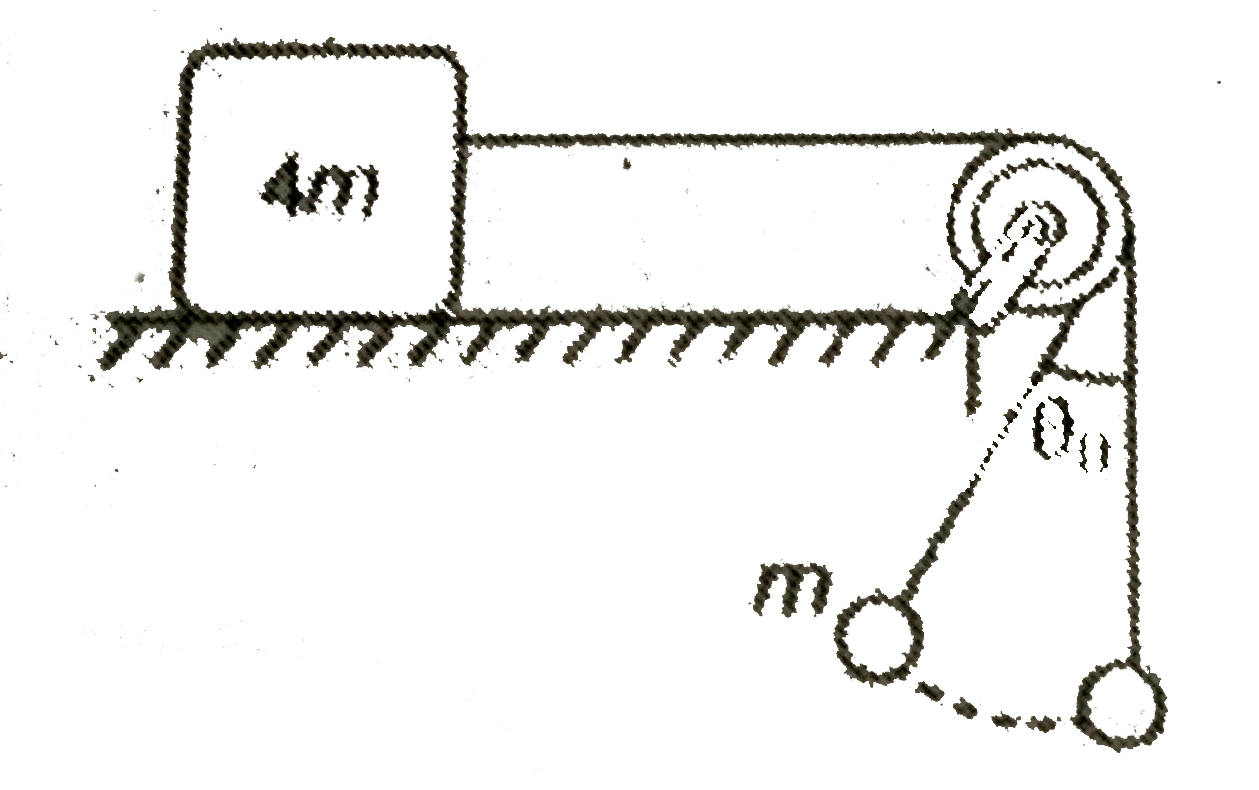
View SolutionTwo bodies of masses m and 4 m are attached with string as shown in the figure. The body of mass m hanging from a string of length l is executing oscillations of angular amplitude θ0 while the other body is at rest. The minimum coefficient of friction between the mass 4m and the horizontal surface should be
View SolutionIn the given figure, a mass M is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is k. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass is in equilibrium position, as shown in the figure, another mass m is gently fixed upon it. The new amplitude of oscillation will be :

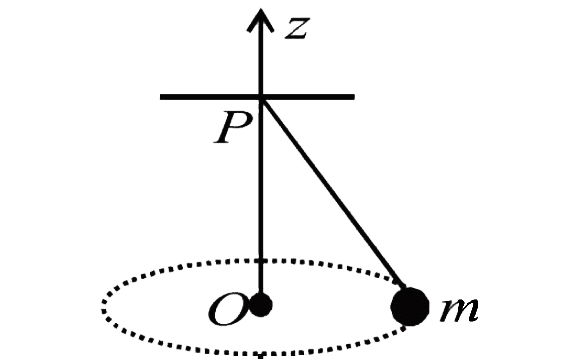
View SolutionA small mass m is attached to a massless string whose other end is fixed at P as shown in the figure. The mass is undergoing circular motion in the x-y plane with centre at O and constant angular speed ω. If the angular momentum of the system. calculated about O and P are denoted. by vacLOandvacP respectively, then.
View SolutionTwo bodies of masses m and 4m are attached to a light string as shown in figure. A body of mass m hanging from string is executing oscillations with angular amplitude 60∘, while other body is at rest on a horizontal surface. The minimum coefficient of friction between mass 4m and the horizontal surface is (here pulley is light and smooth)
View Solution

