A lawn roller is pulled along a horizontal surface through a distance of 20m by a rope with a force of 200N. If the rope makes an angle of 60∘ with the vertical while pulling, the amount of work done by pulling force is
4000 J
1000 J
2000√3J
2000 J
The correct Answer is:C
To solve the problem, we need to calculate the work done by the pulling force on the lawn roller. The work done (W) is given by the formula:
W=F⋅d⋅cos(θ)
where:
- F is the force applied,
- d is the distance moved,
- θ is the angle between the force and the direction of motion.
1. Identify the Given Values:
- Force F=200N
- Distance d=20m
- Angle θ=60∘ (with the vertical)
2. Determine the Angle with the Horizontal:
Since the angle is given with the vertical, we need to find the angle with the horizontal. The angle with the horizontal will be:
θhorizontal=90∘−60∘=30∘
3. Calculate the Work Done:
Using the formula for work done:
W=F⋅d⋅cos(θhorizontal)
Substitute the values:
W=200N⋅20m⋅cos(30∘)
4. Calculate cos(30∘):
The cosine of 30 degrees is:
cos(30∘)=√32
5. Substitute cos(30∘) into the Work Done Equation:
W=200⋅20⋅√32
6. Simplify the Equation:
W=200⋅20⋅√32=200⋅10⋅√3=2000√3J
7. Final Answer:
The amount of work done by the pulling force is:
W=2000√3J
- F is the force applied,
- d is the distance moved,
- θ is the angle between the force and the direction of motion.
- Force F=200N
- Distance d=20m
- Angle θ=60∘ (with the vertical)
Since the angle is given with the vertical, we need to find the angle with the horizontal. The angle with the horizontal will be:
θhorizontal=90∘−60∘=30∘
Using the formula for work done:
W=F⋅d⋅cos(θhorizontal)
Substitute the values:
W=200N⋅20m⋅cos(30∘)
The cosine of 30 degrees is:
cos(30∘)=√32
W=200⋅20⋅√32
W=200⋅20⋅√32=200⋅10⋅√3=2000√3J
The amount of work done by the pulling force is:
W=2000√3J
Topper's Solved these Questions
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level- II (C.W)
Explore 68 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level- III (C.W)
Explore 50 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:C.U.Q-Key
Explore 75 Videos
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE IV
Explore 43 Videos
Similar Questions
A man pulls a lawn roller through distance of 20 m with a force of 20 kg weight. If he applies the force at an angle of 60∘ with the ground, calculate the power developed if he takes 1 min in doing so.
View SolutionA child pulls a box with a force of 200 N at an angle of 60∘ above the horizontal. Then the horizontal and vertical components of the force are-
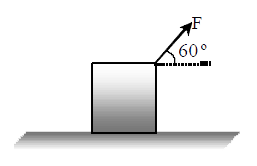
View Solution
Knowledge Check
A lawn roller is displaced through 1km using a force of 200N in a direction making an angle of 60∘ with the lawn .The work down is:
A105JB104JC106JD103JA force F is applied on a lawn move at an angle of 60∘ with the horizontal. If it moves through a distance x, the work done by the force is
AFx/2BF/2xC2FxD2x/FA mass M is suspended by a rope from a rigid support at A as shown in figure. Another rupe is tied at the end B, and it is pulled horizontally with a force. If the rope AB makes an angle θ with the vertical in equilibrium then the tension in the string AB is
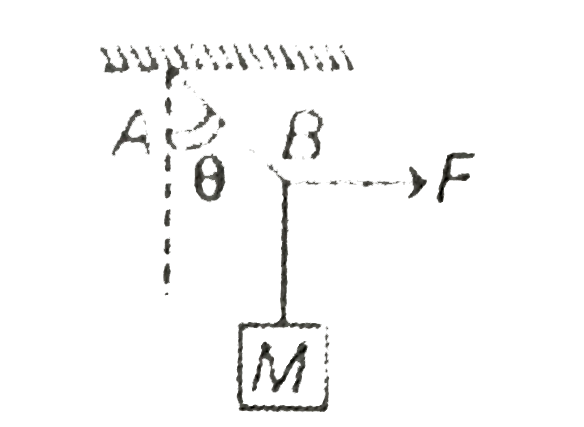 AF sinθBF/sinθCFcosθDF/cosθ
AF sinθBF/sinθCFcosθDF/cosθ
A gardener pushes a lawn roller through a distance of 20 m. If he applies a force of 20 kg wt in a direction inclined at 60∘ to the ground , find the work
View SolutionA body acted upon by a force of 50N is displaced through a distance of 10m in a direction making an angle of 60∘ with the force. Calculate the work done by the force.
View SolutionA body, acted upon by a force of 50N, is displaced through a distance 10m in direction making an angle of 60∘ with the force. Find the work done by the force.
View SolutionA child pulls a rope attached to a stone with a force of 80N. The rope makes and angle of 40∘ to the ground. (i) Calculate the effective value of the pull tending to move the stone along the ground. (ii) Calculate the force tending to lift the stone.
View SolutionWhich of the following statement is/are correct
I in pulling and pushing a roller through 100 m horizontally when a force of 1500 N is acting at an angle of 60∘ with ground the work down is 75 kj.
II work done by F in producing displacement s is given by F ..
View Solution

