Find the area of the greatest rectangle that can be inscribed in an ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$

Video Solution

Text Solution

Verified by Experts

Reactangle can be inscribed in the ellipse with its sides parallel ot axes of theellipse as shown in the following figure.

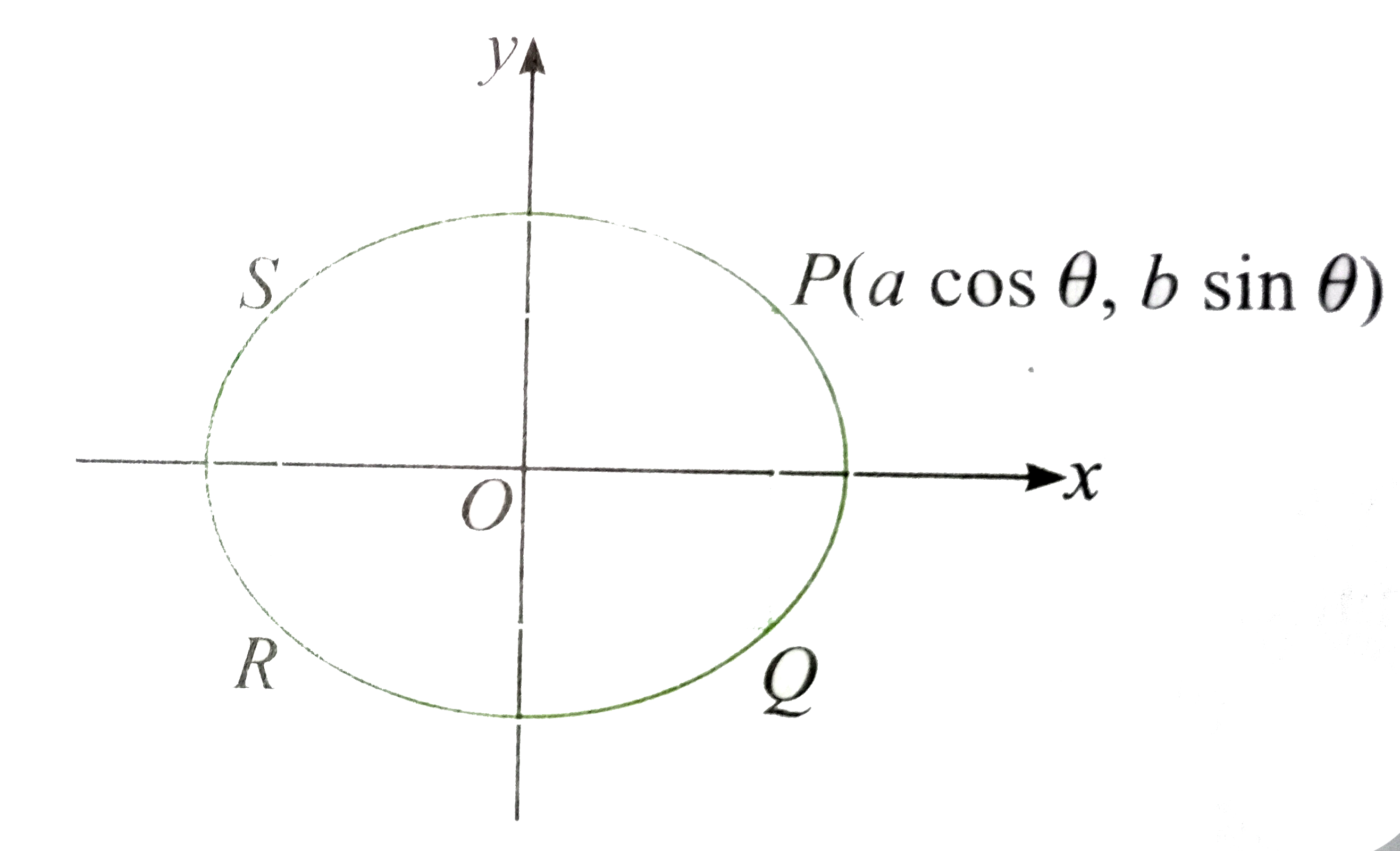
Let $P \equiv (a cos θ, b sin θ)$
$∴$ Area o reactangle PQRS
$= (2 a cos θ) (2 b sin θ)$
$= 2 a b sin 2 θ$
This is maximum when $sin 2 θ = 1$
Henece, maximum area $= 2 a b (1) = 2 a b$

|

Updated on:21/07/2023

Class 11 MATHS ELLIPSE

Similar Questions

Knowledge Check

Question 1 - Select One
Find the area of the greatest rectangle that can be inscribed in an ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$
A $\sqrt{a b}$
B $a / b$
C $2 a b$
D $a b$
Question 2 - Select One
Consider an ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$
What is the area of the greatest rectangle that can be inscribed in the ellipse?
Aab
B2ab
Cab/2
D $\sqrt{a b}$
Question 3 - Select One
The sides of the greatest rectangle that can be inscribed in the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ are
A $a \sqrt{2}, b \sqrt{2}$
B $\sqrt{a}, \sqrt{b}$
Ca,b
D $\frac{a}{\sqrt{2}}, \frac{b}{\sqrt{2}}$

Recommended Questions

Home
Ask Doubt
Profile