If wavelength $4500 Å$ and $6000 Å$ are found to be missing in the reflected spectrum in thin air film interference, the thickness of the film for normal incidence is nearly

A

$9000 Å$

B

$10500 Å$

C

$5250 Å$

D

$4240 Å$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

For missing wavelength, use condition of minima
$2 μ t - \frac{λ}{2} = (2 n + 1) \frac{λ}{2}$
$2 μ t = (2 n + 1) \frac{λ}{2} + \frac{λ}{2} = (n + 1) λ$
For air $μ = 1, t = (n + 1) \frac{λ}{2}$
$λ = \frac{2 t}{n + 1}$
$n + 1 = \frac{2 t}{λ_{1}}$
$(n - 1) + 1 = \frac{2 t}{λ_{2}}$
(i)-(ii)
$1 = 2 t (\frac{1}{λ_{1}} - \frac{1}{λ_{2}})$
$= 2 t (\frac{1}{4500} - \frac{1}{6000}) = 2 t (\frac{1500}{4500 \times 6000})$
$t = 9000 Å$

|

Updated on:21/07/2023

Class 12 PHYSICS DUAL NATURE OF RADIATION AND MATTER

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
For observing interference in thin films with a light of wave length $λ$ the thickness of the film:
Amay be of any magnitude
Bshould be much smaller than $λ$
Cshould be of the order of $λ$
Dshould be a few thousand times of $λ$
Question 2 - Select One
A parallel beam of white light is incident on a thin film of air of uniform thickness. Wavlength $7200 Å$ and $5400 Å$ are observed to be missing from the spectrum of reflected light viewed normally. The other wavelength in the visible region missing in the reflected spectrum is
A $6000 Å$
B $4320 Å$
C $5500 Å$
D $6500 Å$
Question 3 - Select One
Consider a case of thin film interference as shown.Thickness of film is equal to wavelength of light in $μ_{2}$

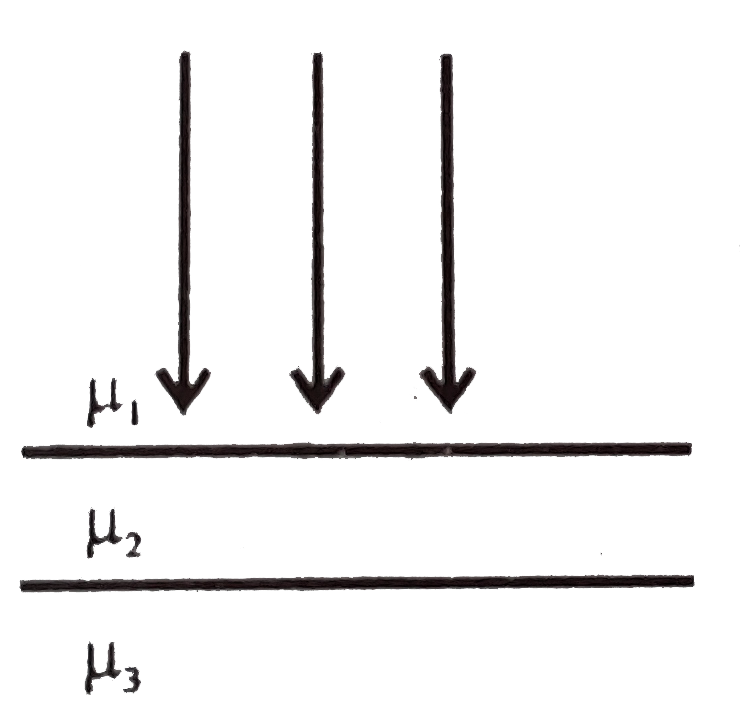AReflected light will be maximum if $μ_{1} < μ_{2} < μ_{3}$
BReflected light will be maximum if $μ_{1} < μ_{2} > μ_{3}$
CTransmitted light will be maxima if $μ_{1} > μ_{2} > μ_{3}$
DTransmitted light will be maximum if $μ_{1} > μ_{2} < μ_{3}$

CP SINGH-WAVE NATURE OF LIGHT-EXERCISES

Home
Ask Doubt
Profile