A ray of light traveling in glass $(μ = 3 / 2)$ is incident on a horizontal glass-air surface at the critical angle $θ_{C}$ . If a thin layer of water $(μ = 4 / 3)$ is now poured on the glass-air surfac, the angle at which the ray emerges into air at the water-air surface is

Video Solution

Text Solution

Verified by Experts

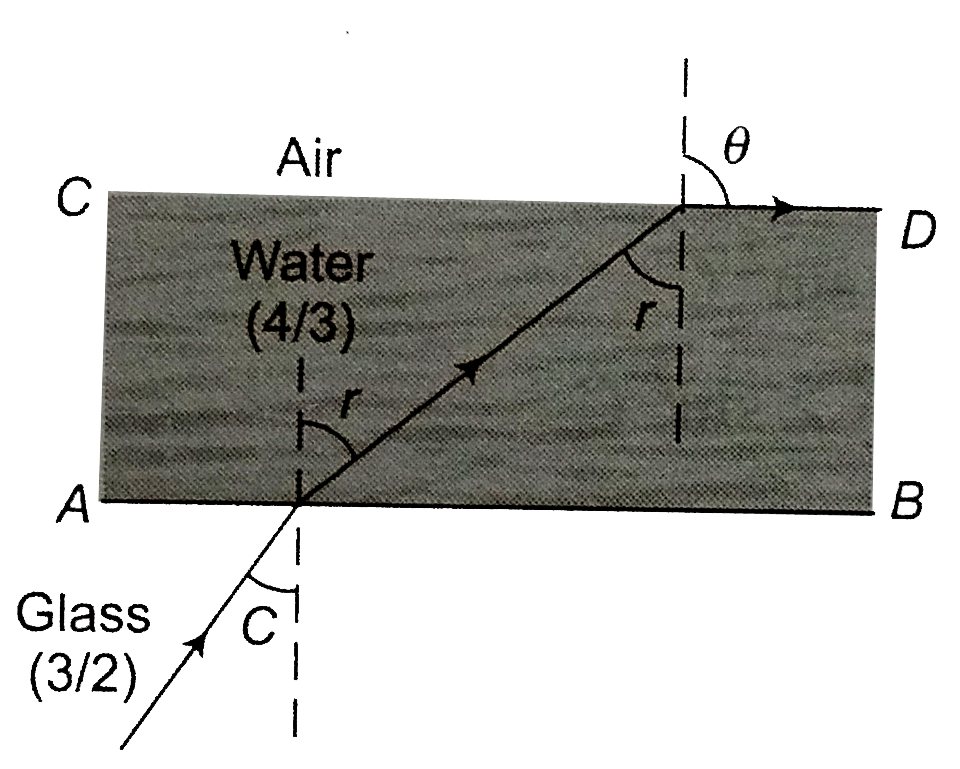
Critical angle for glass-air surface
$μ_{g} sin C = 1 \times {sin 90}^{\circ}$
$sin C = \frac{1}{μ_{g}} = \frac{1}{3 / 2} = \frac{2}{3}$
Refraction at AB
$μ_{g} sin C = μ_{ω} sin r$
$\frac{3}{2} \cdot \frac{2}{3} = \frac{4}{3} sin r$
$sin r = \frac{3}{4}$
Refraction at water-air surface
$μ_{ω} sin r = 1 \times sin θ$
$\frac{4}{3} \times \frac{3}{4} = sin θ = 1$
$θ = 90^{\circ}$
The ray will emerge parallel to water-air surface.

|

Updated on:21/07/2023

Class 12 PHYSICS GEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A ray of light travelling inside a rectangular glass block $(μ = \sqrt{2})$ is incident on the glass-air surface at an angle of incidence of $45^{\circ}$ . The refractive index of air is 1. The ray will
Aemerge into air without any deviation
Bbe reflected back into glass
Cbe absorbed
Demerge into air $r = 90^{\circ}$
Question 2 - Select One
A ray of light travelling from glass to air is incident at $50^{\circ}$ from the glass air boundary . What is the angle of deviation if the critical angle is $42^{\circ}$ ?
A $0^{\circ}$
B $60^{\circ}$
C $80^{\circ}$
D ${sin}^{- 1} [\frac{{sin 50}^{\circ}}{1.5}] - 50$
Question 3 - Select One
A ray of light travelling in water is incident on its surface open to air. The angle of incidence is $θ$ , which is less than the critical angle. Then there will be
Aonly a reflected ray and no refracted ray
Bonly a refracted ray and no reflected ray
Ca reflected ray and a refracted ray and the angle between them would be less than $180 d e g r e e - 2 θ$
Da reflected ray and a refracted ray and the angle between them would be greater than $180 d e g r e e - 2 θ$

CP SINGH-REFRACTION OF LIGHT BY PLANE SURFACES-Exercises

Home
Ask Doubt
Profile