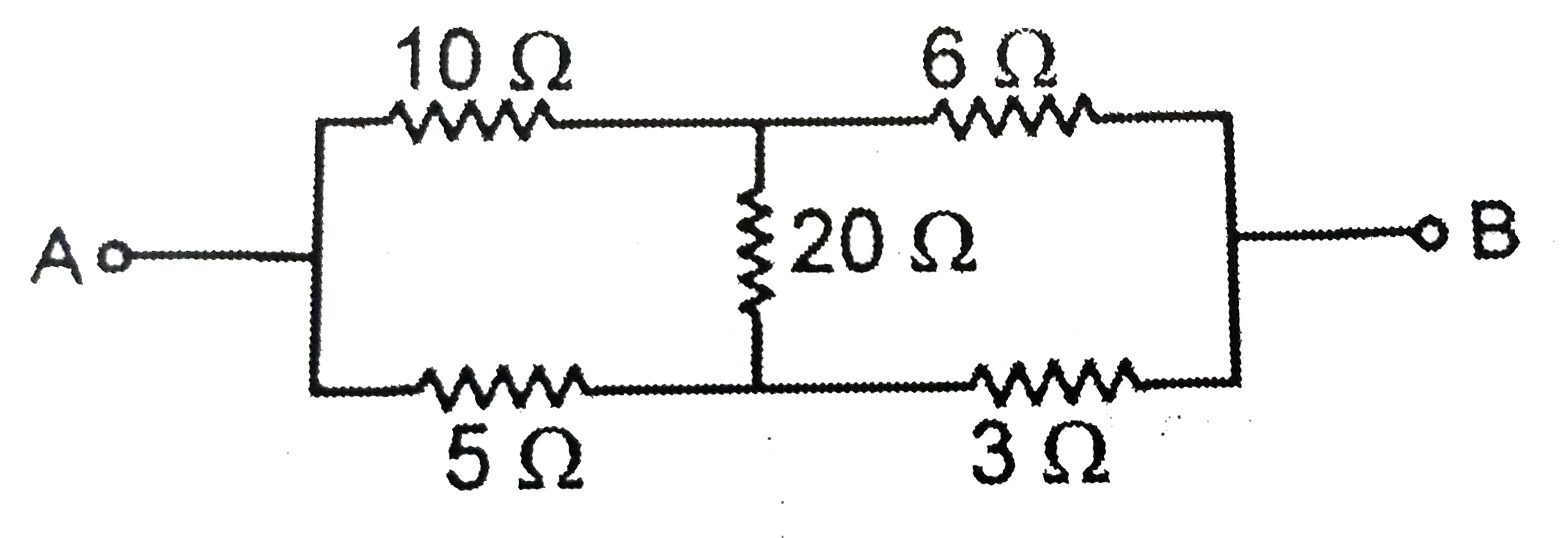
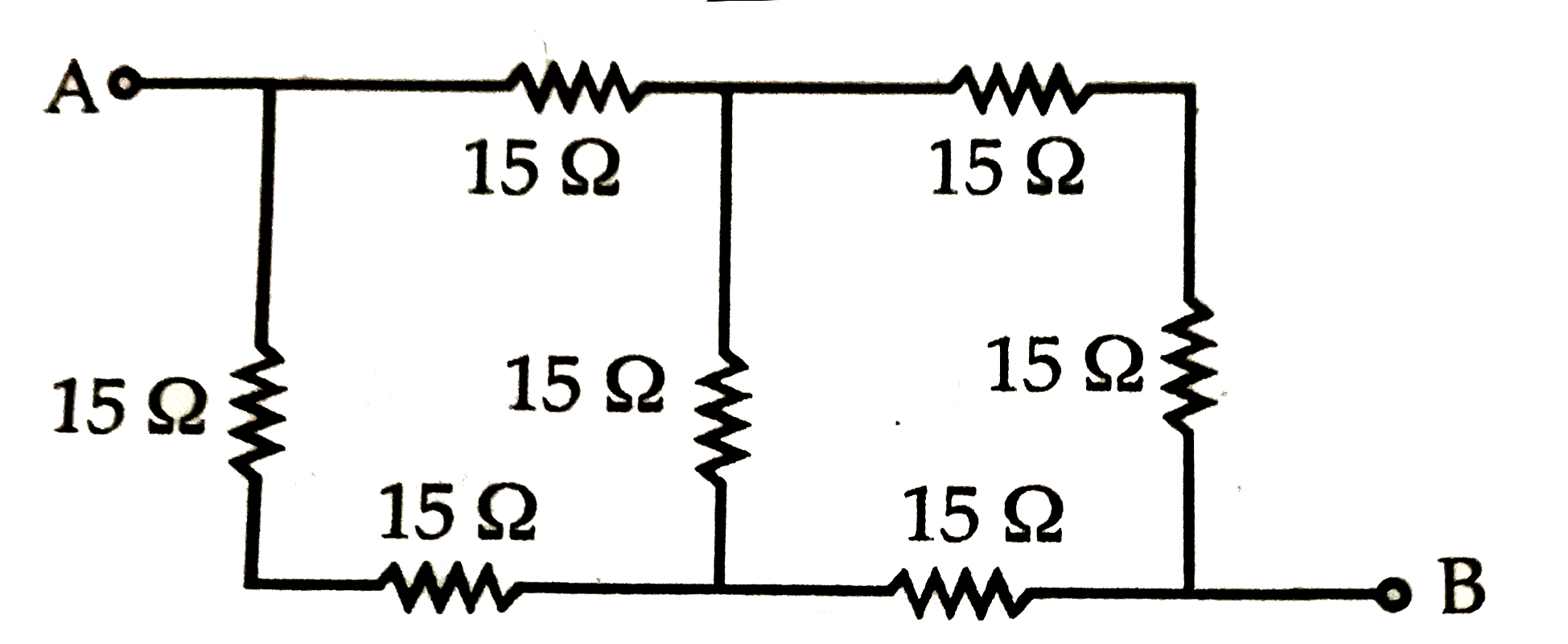Find the equivalent resistance between the terminal points A and B in the network shown in the figure.
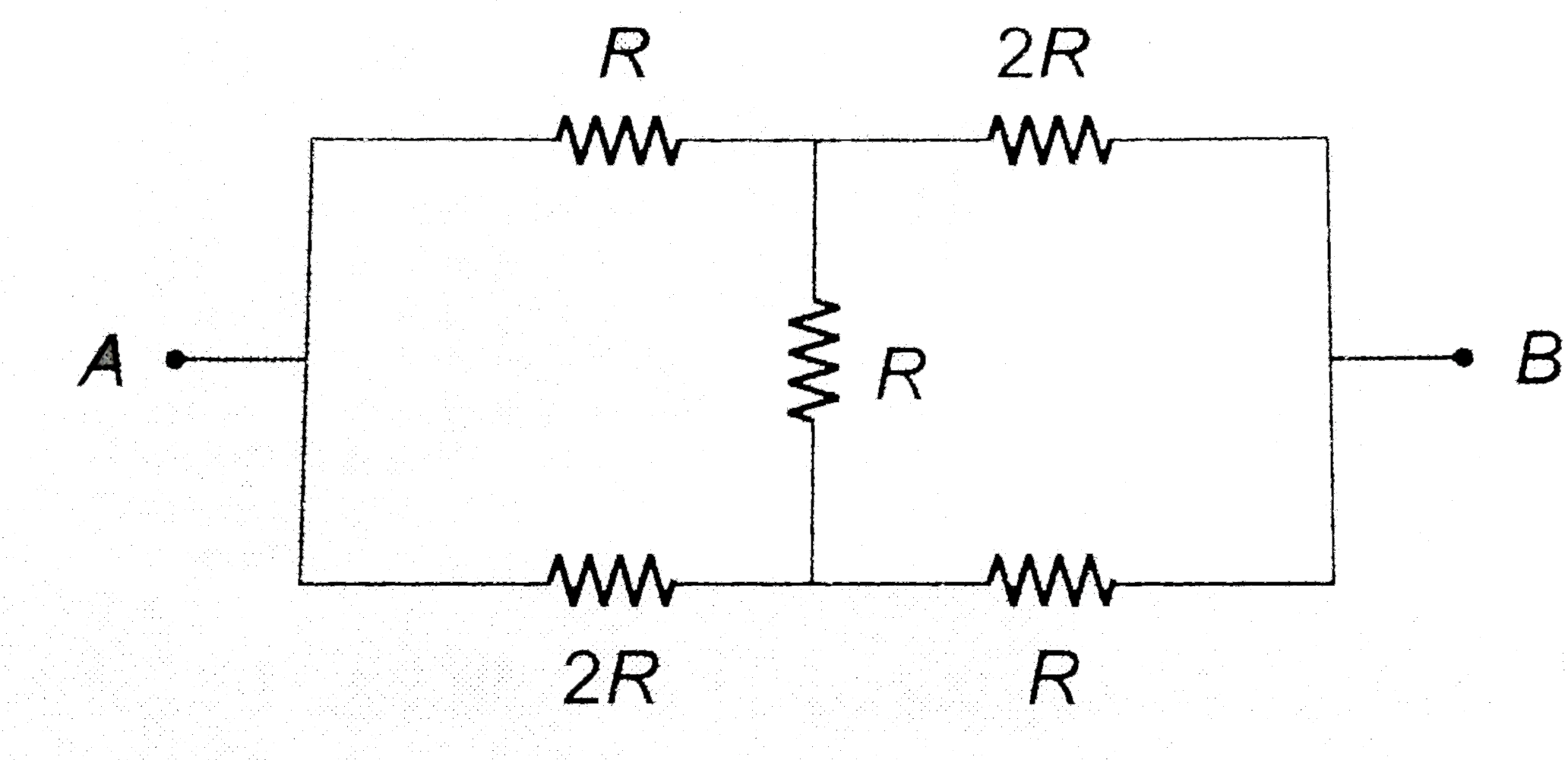 .
.
Video Solution
Text Solution
Here resistance are neither in series nor in parallel. This problem can be solved by Kirchhoff's rules or by delta-star method.
Equivalent resistance by Kirchhoff's rules : First, connect a battery of emf E between points A and B, let the current supplied by battery is i, then find the value of E/i in terms of R.
Req=Ei

Here we are making use of symmetry in current distribution. i1 is entering in R between A and C and i1 will flow in R between D and B. Similarly i−i1 will enter in 2R between A and D and i−i1 will flow in 2R between C and B.
The current in middle resistance R between C and D
i1=x+i−i1⇒x=2i1−i
Lo op ①, A to A, path ACDA
VA−i1R−(2i1−i)R+(i−i1)2R=VA
−5i1+3i=0⇒i1=3i/5
Lo op ②, A to A, path ADBA
VA−(i+i1)3R−i1R+E=VA⇒7R5=Ei=Req
Req=7R5
Equivalent resistance by delta-star method :

Convert delta ACD into a star
x=R.2R∑R=R+2R+R=2R24R=R2
y=R.R∑R=R24R=R4
z=R.2R∑R=2R24R=R2
We have new circuit as
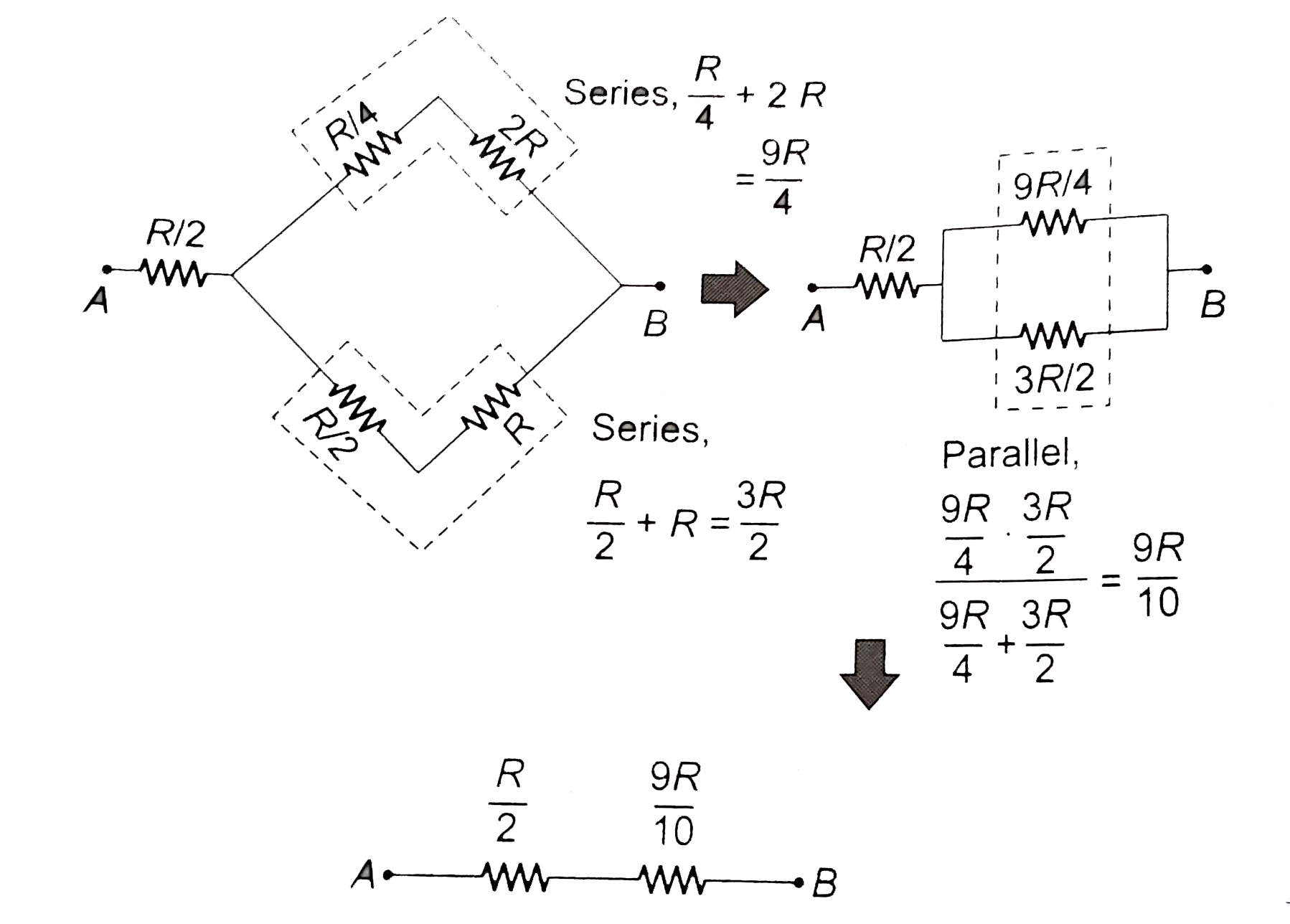
Req=R2+9R10=5R+9R10=14R10=7R5.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
What is the equivalent resistance between the points A and B of the network.
 .A2 RB4R3C2R3DR
.A2 RB4R3C2R3DR
What is the equivalent resistance between the terminal points A and B in the cirucit shown in figure-3.84
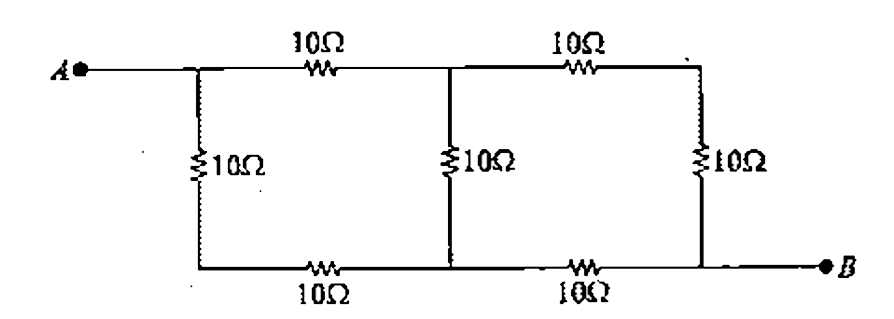
View Solution
Find the equivalent resistance between the terminals A and B in the network shown figure. Given each resistor R of 10Ω.
View SolutionCalculate the resistance between the terminals A and B of the network shown in fig
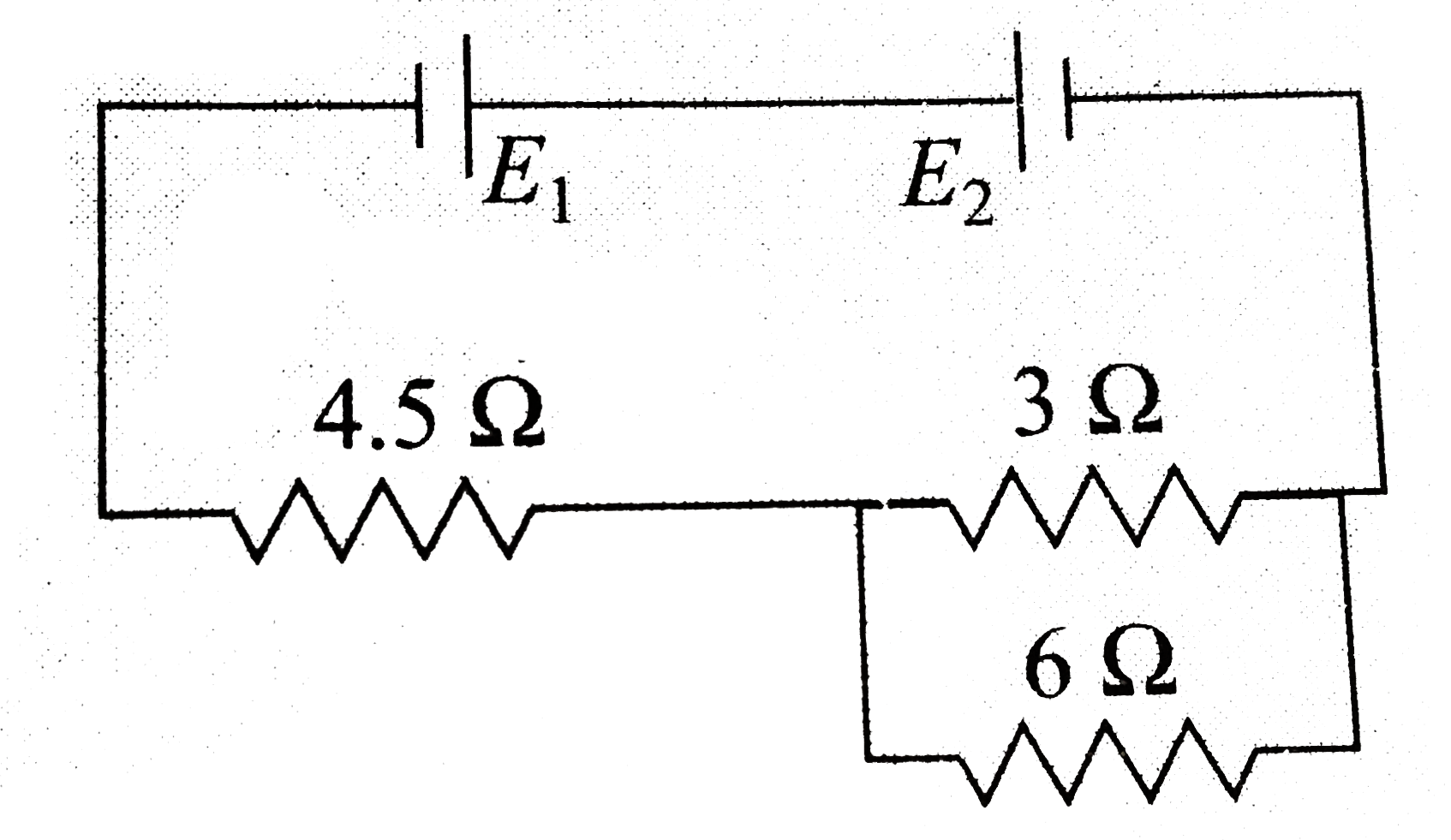
View SolutionCalculate the equivalent resistance between the points A and B of the network shown in figure

View SolutionCalculate the equivalent resistance between the points A and B of the network shown in figure
View Solution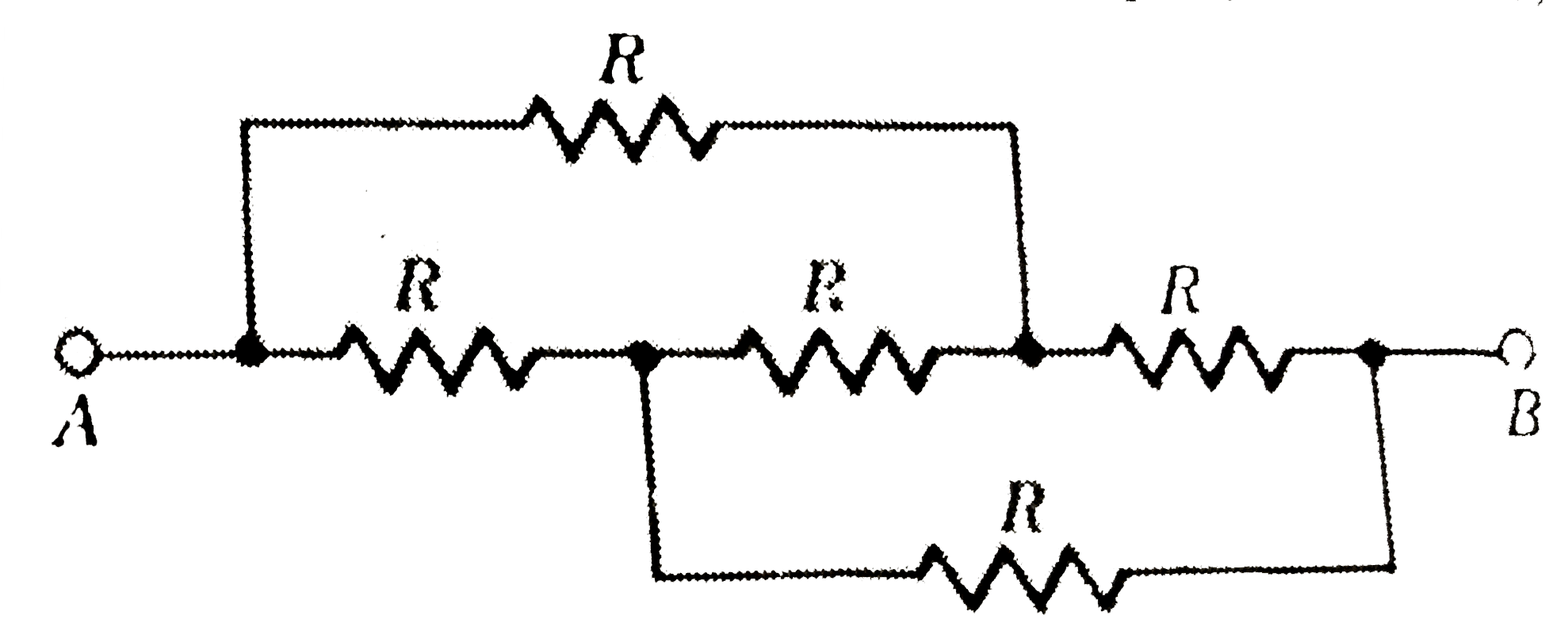
Calculate the equivalent resistance between the points A and B of the network shown in figure.
View SolutionFind equivalent resistance of the between the terminals A and B.
View Solution