1 meter long metallic wire is broken into two unequal parts PandQ.P part of the wire in uniformly extended into another wire R. Length of R is twice the length of P and the resistance of R is equal to that of Q. Find the ratio of the resistance P and R and also the ratio of the length PandQ
Since mass or volume of wire remains same when area or length of wire is changed. For solving these problems. Keep in mind that volume of wire remains same.
⋅ For % change, use (final valueinitial value−1)×100
⋅ If necessary, use binomial theorem to solve
(a) (i) A1l1=A2l2
Al=A2.2l⇒A2=A/2
R1=ρlA,R2=ρl2A2=ρ.2lA/2=4ρlA
R2=4R
(ii) A1l1=A2l2
Al=2Al2⇒l2=l/2
R1=ρlA,R2=ρl2A2=ρl/22A=ρl4A
R2=R4
(b) A1l1=A2l2
πr2l=π(2r)2l2⇒l2=1/4
R1=ρlπr2,R2=ρl2A2=ρl/44πr2=116ρlπr2
R1R2=16
( c) l1=l,A1=A,l2=l(1+0.1/100),A2=A'
A1l1=A2l2⇒Al=A'l(1+0.1/100)
A'=A(1+0.1/100)
R=ρlA,R'=ρl2A2=ρl(1+0.1/100)A/(1+0.1/100)=ρlA(1+0.1100)2
R'R=(1+0.1100)2=1+2×0.1100=1+0.2100
R'R−1=0.2100
% change =(R'R−1)×100=0.2100×100=0.2%
(d) l1=l,A1=A
l1=l(1+25100)=5l4,A2=A'
A1l1=A2l2
Al=A'5l4⇒A'=4A5
R2R1=ρl2A2ρl1A1=l2l1.A1A2=5l/4l.A4A/5=2516
(R2R1−1)×100=(2516−1)×100=90016=56.25%
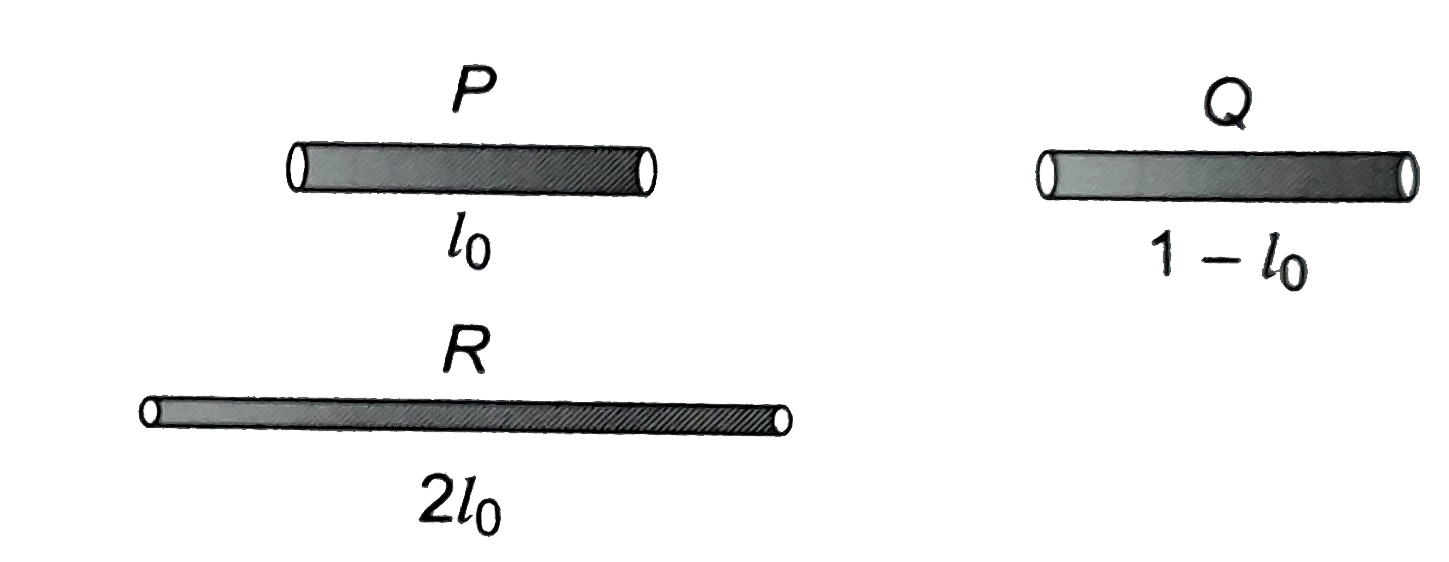
(e) Let length of Pto l0
Rp=ρl0A,RQ=ρ(1−l0)A
RR=ρ.2l0A/2
=4ρl0A [since, P, is converted i nt o, R, by, doubli ng],[its l eng ths, hence, area, of R, becomes, half]
RpRR=14
RQ=RR⇒(1−l0)=4l0⇒l0=0.2m
lplQ=0.21−0.2=12
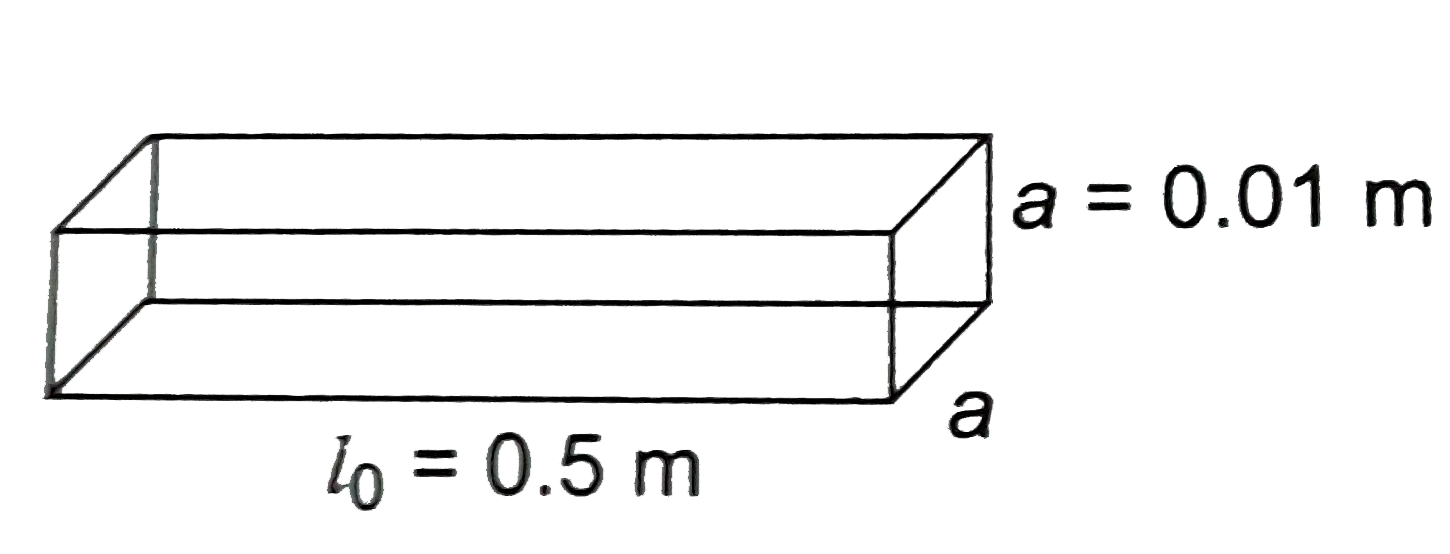
(f) (i) Between square faces l=l0,A=a×a
R=ρlA=ρl0a2=50×10−8×0.50.01×0.01=2.5×10−3Ω
(ii) Between rectangular faces l=a,A=l0×a
R=ρlA=ρal0a=ρl0=50×10−80.5=10−6Ω
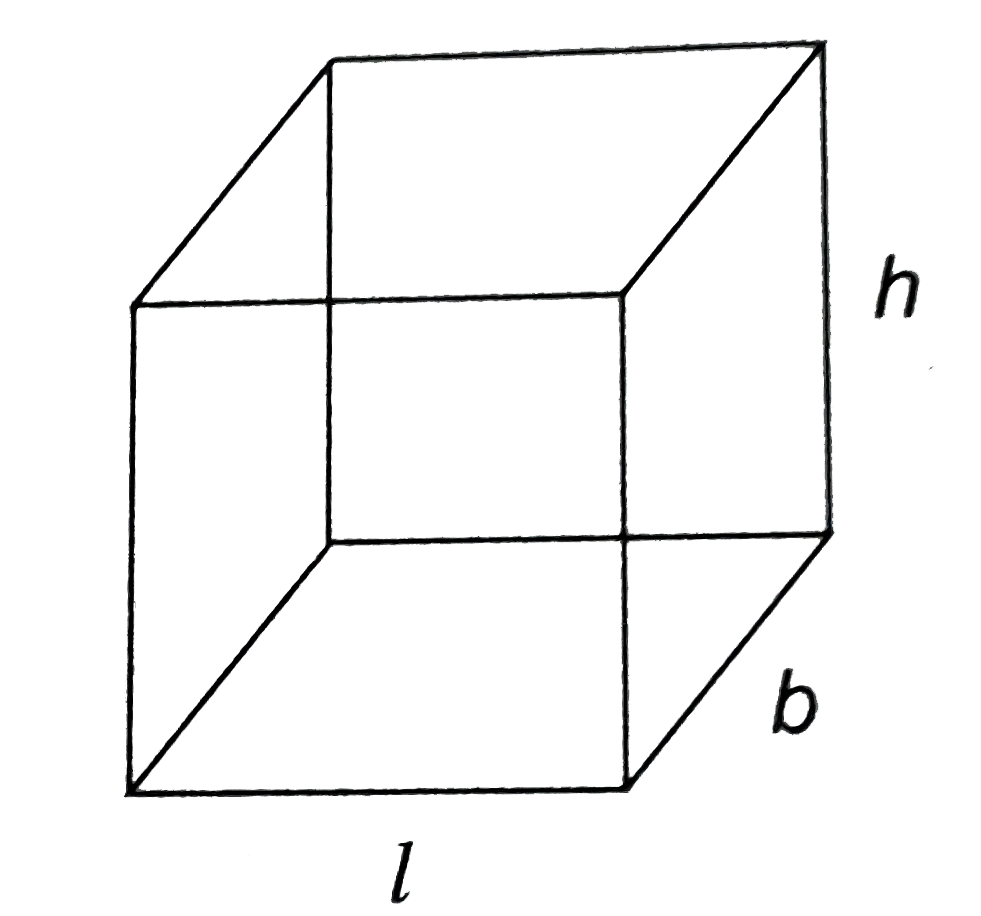
(g) Resistance between faces of area
(i) (l×b),R1=ρhlb
(ii) (b×h),R2=ρlbh=Rmax
(iii) (l×h),R3=ρbl×h=Rmin
RmaxRmin=l2b2=(4b)2b2=16
(h) m1=m,m2=3m,m3=5m
l1=5l,l2=3l,l3=l
Density and resistivity of each wire is same. Here d : density of wire and ρ : resistivity of wire.
Mass = density × volume = density × area × length
Mass α(area×length)
m1=m=kA1l1=kA15l⇒A1=m5kl=λ5
m2=3m=kA2l2=kA2.3l⇒A2=mkl=λ
m3=5m=kA3l3=kA3.l⇒A3=5mkl=5λ
R1:R2:R3:=l1A1:l2A2:l3A3
=5lλ/5:3lλ:l5λ
=25:3:1/5
=125:15:1.
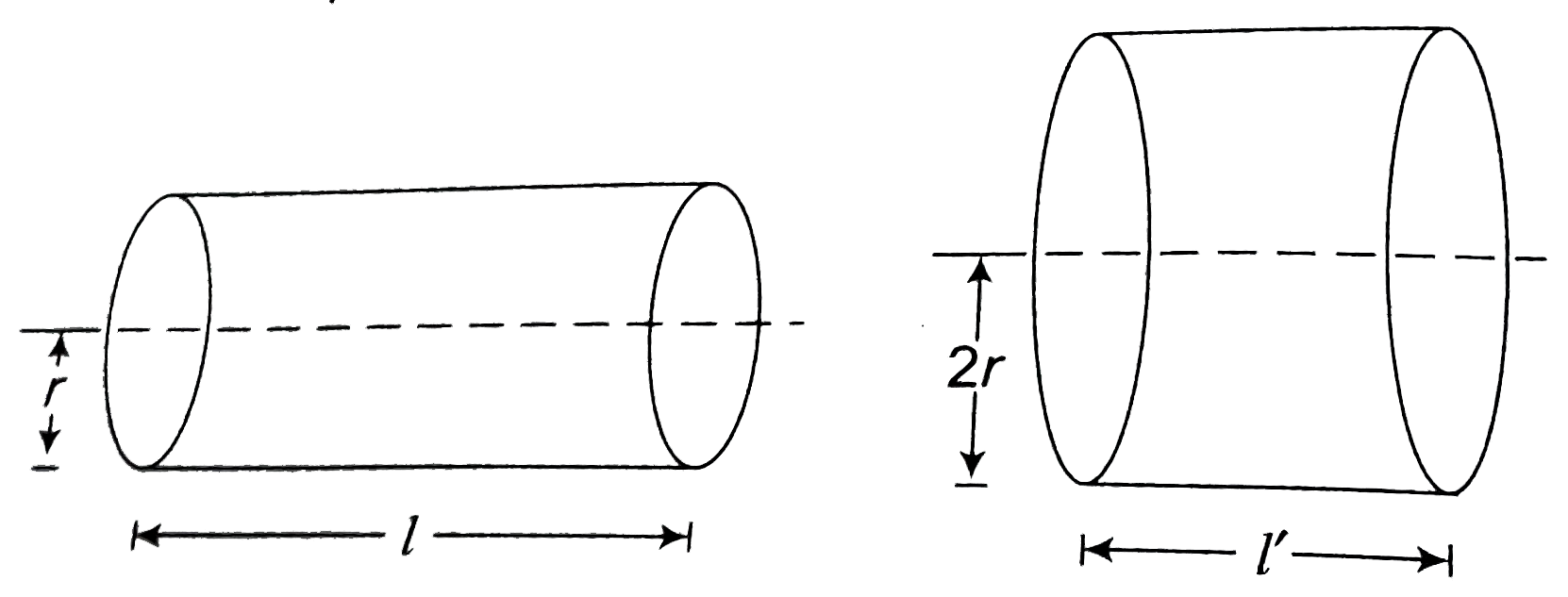
Topper's Solved these Questions
Similar Questions
One metre long metallic wire is broken into two unequal parts P and Q. The part P is uniformly extended into another wire R. Find the ratio of the resistances of P and R and also the ratio of the lengths P and Q.
View SolutionIn comparing the resistance of two cells PandQ with a sides wire bridge, a balance point is obtained when the sliding contact is 30cm from the zero end of the wire. The resistances PandQ are interchanged and the balance is obtained at 120cm from the same emf. Find the ratio of the resistance PandQ and the length of the bridge wire
View Solution
Knowledge Check
A wire P has resistance of 20 ohm. Another wire Q of same material but length twice that of P has resistance of 8 ohm. If r is the radius of cross-section of P, the radius of cross-section of Q is
ArBr√2Cr√5D2rP,Q and R are three partners in a business. If Ps capital is equal to twice the capital of Q and Qs capital in three times the capital of R, find the ratio of the capitals of P,Q and R.
A6:3:1B1:3:6C2:3:6D3:6:1Specific resistance of gold wire is p. If the length of wire is increased the twice of previous length, then its specific resistance will be
AρB2ρCρ/2Dρ/4
There are two wires P and Q made of the same material and both have the same mass . The radius of wire P is half the radius of the wire Q. the resistance of P is 24Ω. Find the resistance of Q.
View SolutionA given piece of wire of length l and radius r and resistance R is stretched uniformly to wire of radius r2 .Its new resistance is:
View SolutionA wire made of material A has resistance R1 another wire made of material B having P time the length and q times the radius of first wire has resistance R2 . If resistivity of B is r times that of A, then calculateR2/R1 .
View Solution{(p∧(p→q))∧(q→r)}→r is equal to
View SolutionWith resistances P and Q in the left and right gaps of a metre bridge respectively, the null point divides the wire in the ratio 1 : 2 . If P and Q are increased by 20Ω each, the null point divides the wire in the ratio 3 : 4, then the resistances P and Q are given as :
View Solution
