Question

From the foot of a tower $80m$ high, a stone is thrown up so as to reach the top of a tower. After $2s$, another stone is dropped from the top of the tower. When and where the two stones meet?

Explanation

First, we have to calculate the intial velocity of the projected stone. When it reaches the top of the tower, i.e. at height `80 m`, its velocity becomes zero.
`0=u^(2)-2gxx80impliesu=40 m//s`
let the stones meet t seconds after projection of the first. The dropped stone or second stone will take `(t-2)` seconds. Let the stones meet at height h.

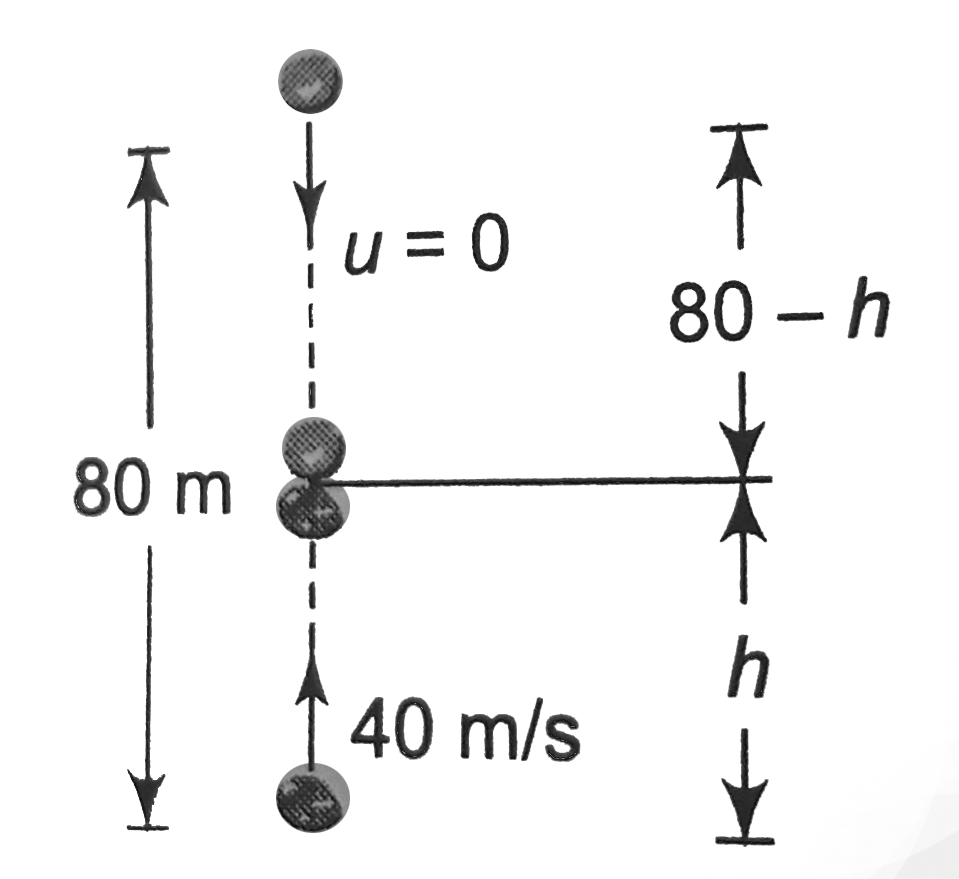
First stone: `h=40t-1/2g t^(2) ...(i)`
Second stone: `80-h=1/2g(t-2)^(2) ...(ii)`
Adding (i) and (ii), we get
`80=40t-1/2g[t^(2)-(t-2)^(2)]`
`=40t-5(2t-2)(2)=40t-20t+20`
`20t=60impliest=3 s`
`h=40t -1/2g t^(2)=40xx3-5xx(3)^(2)`
`=120-45=75 m`
The stones meet at height `75 m` and after `3s` from the projection of the first stone.
Note: Till now we have taken those problem in which the partical is moving in one direction (either upward or downward). For these problems, we have assumed vertically downward//upward direction positive according to our convenience.
In some of the following problems, the particle is moving in both the directions, upward direction followed by downward direction. For these type of problems, we will assume vertically upward direction positive, displacement above origin positive and below origin negative.