A train starts from station $A$ with uniform acceleration $a_{1}$ . For some distance and then goes with uniform retardation $a_{2}$ for some more distance to come to rest at station $B$ . The distance between stations $A$ and $B$ is $4 k m$ and the train takes $1 / 5 h$ to compete this journey. If accelerations are in km per minute unit, then show that $\frac{1}{a_{1}} + \frac{1}{a_{2}} = x$ . Find the value of $x$ .

Video Solution

Text Solution

Verified by Experts

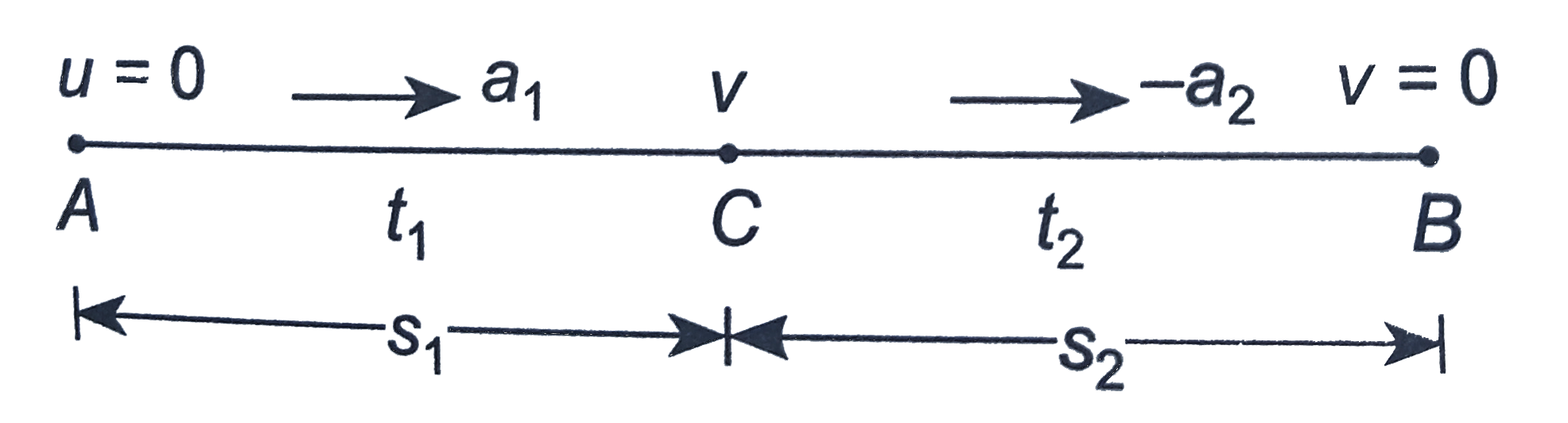
$A$ to $C$ : $v = 0 + a_{1} t_{1} \dots (i)$
$v^{2} = 0 + 2 a_{1} s_{1} \dots (i i)$
$C$ to $B$ : $0 = v - a_{2} t_{2} \dots (i i i)$
$0 = v^{2} - 2 a_{2} s_{2} \dots (i v)$
Given
$t_{1} + t_{2} = 4 \dots (v)$
$s_{1} + s_{2} = 4 \dots (v i)$
From (i), (ii) and (v)
$\frac{v}{a_{1}} + \frac{v}{a_{2}} = 4$
$v = \frac{4}{\frac{1}{a_{1}} + \frac{1}{a_{2}}}$
From (ii), (iv) and (vi)
$\frac{v^{2}}{2 a_{1}} + \frac{v^{2}}{2 a_{2}} = 4$
$\frac{v^{2}}{2} (\frac{1}{a_{1}} + \frac{1}{a_{a}}) = 4$
$\frac{1}{2} . \frac{4^{2}}{{(\frac{1}{a_{1}} + \frac{1}{a_{2}})}^{2}} . (\frac{1}{a_{1}} + \frac{1}{a_{2}}) = 4$
$\frac{1}{a_{1}} + \frac{1}{a_{2}} = 2$
or $s_{1} + s_{2} = \frac{1}{2} a_{1} t_{1}^{2} + \frac{1}{2} a_{2} t_{2}^{2} = \frac{1}{2} a_{1} t_{1} t_{1} + \frac{1}{2} a_{2} t_{2} t_{2}$
$= \frac{v}{2} (t_{1} + t_{2})$
$4 = \frac{v}{2} (4) \Rightarrow v = 2$
$t_{1} + t_{2} = \frac{v}{a_{1}} + \frac{v}{a_{2}} = v (\frac{1}{a_{1}} + \frac{1}{a_{2}})$
$4 = 2 (\frac{1}{a_{1}} + \frac{1}{a_{2}}) \Rightarrow \frac{1}{a_{1}} + \frac{1}{a_{2}} = 2$

Updated on:21/07/2023

A train starts, from station A with uniform acceleration $f_{1}$ for some distance and then goes with uniform retardation $f_{2}$ for some more distance to come to rest at station B. The distance between the stations A and B is 4 km and the train takes 4 minutes to complete this journey. If $f_{1}$ and $f_{2}$ are in km-minute units, then $\frac{1}{f_{1}} + \frac{1}{f_{2}} =$
A1
B2
C3
D4
The distance between two stations is 240 km. A train takes 4 hours to cover this distance. Calculate the speed of the train.
A40 km $h^{- 1}$
B50 km $h^{- 1}$
C60 km $h^{- 1}$
D70 km $h^{- 1}$
A train starts from rest and moves with uniform acceleration $α$ for some time and acquires a velocity $v$ it then moves with constant velocity for some time and then decelerates at rate $β$ and finally comes to rest at the next station. If L is distance between two stations then total time of travel is
A $\frac{L}{V} + \frac{V}{2} (\frac{1}{α} + \frac{1}{β})$
B $\frac{L}{V} - \frac{V}{2} (\frac{1}{α} + \frac{1}{β})$
C $\frac{L}{V} - \frac{V}{2} (\frac{1}{α} - \frac{1}{β})$
D $\frac{L}{V} + \frac{V}{2} (\frac{1}{α} - \frac{1}{β})$