Escribed Circle
Step by step video & image solution for Escribed Circle by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
If H is orthocentre of acute angled triangle ABC, then image of H with respect to side AB always lies on (1) Circumcircle of △ABC (2) Circumcircle of △AHB (3) Escribed circle opposite to vertex C (4) Circumcircle of △AIB where I is incentve △ABC
View SolutionIn the following diagram there are three circles packed in another circle, such that each circle is tangent to all other circles in this arrangement. The radius of the circumscribing circle A is 1 cm, and circle B and circle C are congruent. Find the radius of the circle D.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The figure shows a rectangle ABCD with a semi-circle and a circle inscribed inside it as shown. What is the ratio of the area of the circle to that of the semi-circle ?
 A(√2−1)2B2(√2−1)2C(√2−1)2D2(√2−1)4
A(√2−1)2B2(√2−1)2C(√2−1)2D2(√2−1)4 - Question 2 - Select One
Find the radius of the circle escribed to the triangle ABC (Shown in the figure below) on the side BC if ∠NAB=30∘,∠BAC=30∘,AB=AC=5.
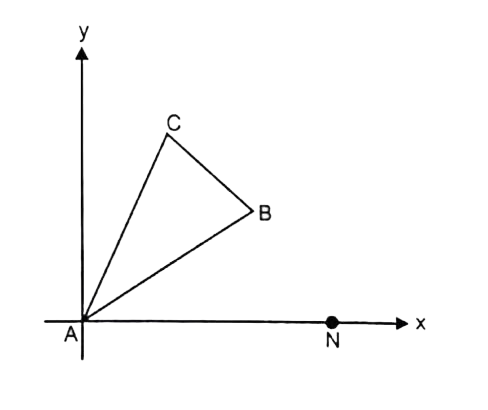 A(10√2+5√3−5)(2−√3)2√2B(10√2+5√3+5)2√2(2−√3)C(10√2+5√3−5)2√2(2+√3)D(10√2+5√2+1)2√3(√3−1)
A(10√2+5√3−5)(2−√3)2√2B(10√2+5√3+5)2√2(2−√3)C(10√2+5√3−5)2√2(2+√3)D(10√2+5√2+1)2√3(√3−1)
Circle K is inscribed in the first quadrant touching the circle radius of the circle K, is-
View SolutionBasic OF circle || General form OF circle || Circumference || Questions based on Circle
View SolutionIn a ΔABC, if (II1)2+(I2I3)2=λR2, where I denotes incentre, I1,I2andI3 denote centres of the circles escribed to the sides BC, CA and AB respectively and R be the radius of the circum circle of ΔABC. Find λ.
View SolutionIn a ΔABC, if (II1)2+(I2I3)2=λR2, where I denotes incentre, I1,I2andI3 denote centres of the circles escribed to the sides BC, CA and AB respectively and R be the radius of the circum circle of ΔABC. Find λ.
View SolutionThe triangle ABC is a right angled triangle, right angle at A. The ratio of the radius of the circle circumscribed to the radius of the circle escribed to the hypotenuse is, √2:(√3+√2). Find the acute angle B & C. Also find the ratio of the sides of the triangle other than the hypotenuse.
View SolutionWhat Is Circle ?|Parts Of A Circle|Terms Related To Circles|Sector Of A Circle|Segment Of A Circle|NCERT Exercise
View Solution

