Cube
Cube
In this chapter, we will discuss the cube, which is one of the most interesting topics in geometry, and its properties. In Geometrical Maths, a Cube is a solid three-dimensional figure that has got 8 vertices, 6 square faces along with 12 edges. It is also termed as a regular hexahedron. If you wish to get the real-life example of a cube, them 3 x 3 Rubik’s cube is the best one. You can also take another example like 6 sided dices as well that proves to be the exact example of a cube. Well, here you would be able to learn the definition of the cube, its properties and also its importance in Maths. We will also look forward to understanding the volume area and the surface area formula for the cube.
You should keep in mind that when it comes to Solid Geometry, it all revolves around the three-dimensional shapes and figures that have got figures and shapes. The other types of solid shapes are;
- Cylinder
- Cuboid
- Cone
- Sphere
Definition of Cube
As we have discussed earlier that a cube is a 3D solid shape with 8 vertices, 6 square faces along with 12 edges, it all meet at one vertex point. It is important to have the right understanding that it is also known as an equilateral cuboid, square parallelepiped and a right rhombohedron.
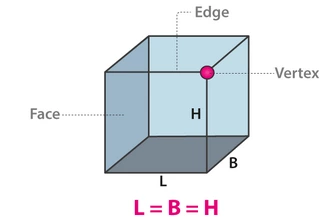
Look at the above figure of a cube. Here, you can see a face, edge, the vertex of the cube. In this case, the length is defined as ‘L’, breadth is defined as ‘B’ and height as ‘H.’ So, the edges of the cube which is represented by the length, breadth and area connects at a single point which is known as the vertex. The four vertices connect the faces of the cube.
Now, we will discuss the properties of the cube where we will also understand the formula for cube volume and surface area.
Formulae For Cube
We have come to know about the properties and definitions of the cube that has got an important role to play in Solid Geometry. So, we will go further to have a good understanding of the two major formulas for a solid shape which are surface area and volume.
Surface area of the cube
It is known that for any shape the area is defined as the region which is occupied by it in a plane. Since a cube is a three-dimensional object, so the area which is occupied it will be in the form of a 3D plane. Having six faces in a cube, thus it is required to calculate the surface area of the cube which is covered by each face.
The formula for surface area is:
Surface Area of Cube = 6a2 in a square units
Volume of Cube
The space that can be contained in a cube is called a volume of a cube. Let’s for example, if we need to immerse a cubical shape object in water, then the volume calculates the object. Here, you should know that the formula of the volume is:
Volume of cube = a3 cubic units
Length of Diagonal of Cube
Suppose the length of the side is ‘a’, then,
- Length of the Diagonal of Cube = √3 a
- Length of the Diagonal of Face of the Cube = √2 a
Properties of Cube
- All its faces are in the shape of a square.
- Equal dimensions can be found in all the faces or sides.
- Each of the faces meets the other four faces.
- The edges opposite to each other are always parallel.
- The plane angles of the cube which are found are the right angle.
- The three faces and three edges are met by each of the vertices.
Related Videos:
- Cuboid
- Right Circular Cylinder
- Right Circular hollow cylinder
- Right Circular Cone
- Sphere and Hemisphere
Solved Example on Cube
Example 1
Suppose the value of the side of the cube is 20cm, can you find its surface area and volume?
Solution:
Given, side, a = 20cm
Using the surface area and volume formula of the cube, we get:
Surface Area = 6a2 = 6 × 202 = 6 × 400= 2400 cm2
Volume = a3 = 203 = 8000 cm3
Example 2
The four walls, as well as the base of a rectangular tank, have got dimensions of 3 m × 2 m × 2.5 m. Can you find the cost of painting it at the rate of Rs 4.50 per m2?
Solution:
Given:
(l) length = 3 m
(b) breadth =2 m
(h) height = 2.5 m
Area of four walls and base
= 2 (l + b)h +lb
= 2(3 + 2)2.5 + 3 x2
= 31 cm2
Cost of painting 1m2 = Rs 4.50
Therefore, the cost of painting 31 m2 =Rs (31 × 4.50)
= Rs 139.50
Example 3
A concrete pillar has a height of 15 m. It has a cross-section of square of side 3 m. Can you find out the cost of the painting of its top and four walls at the rate of Rs 4 per m2?
Solution:
Given:
(l) length = 3 m
(b) breadth = 3 m
(h) height = 15 m
Area of four walls and top
= 2 (l + b)h +lb
= 2(3 + 3)15 + 3 x 3
= 189 m2
Cost of painting 1m2 = Rs 4
Therefore, the cost of painting 189 m2 =Rs (189 × 4)
= Rs 756
Example 4
The dimension of the tank that is found inside has 8 m × 5 m × 4 m. If there is a requirement to line the inside of a rectangular tank on the sides and bottom, then how many m2 would be required?
Solution:
Given:
(l) length = 8 m
(b) breadth = 5 m
(h) height = 4 m
Area of four walls and base
= 2 (l + b)h +lb
= 2(8 + 5)4 + 8 x 5
= 144 m2
Therefore, in order to line the inside of the tank, 144 m2 is required.
Important Chapters:

Similar Questions
Knowledge Check
Following frightening diagrams show identical cubes such that edge of cube 2 lies exactly in the middle of one of the faces of Cube 1 and Cube 4 has a corner at the body centre of the cube 3 . Find the contribution (in fraction) of the spheres shown to each of the cube 1 ,2 , 3 and 4 respectively is
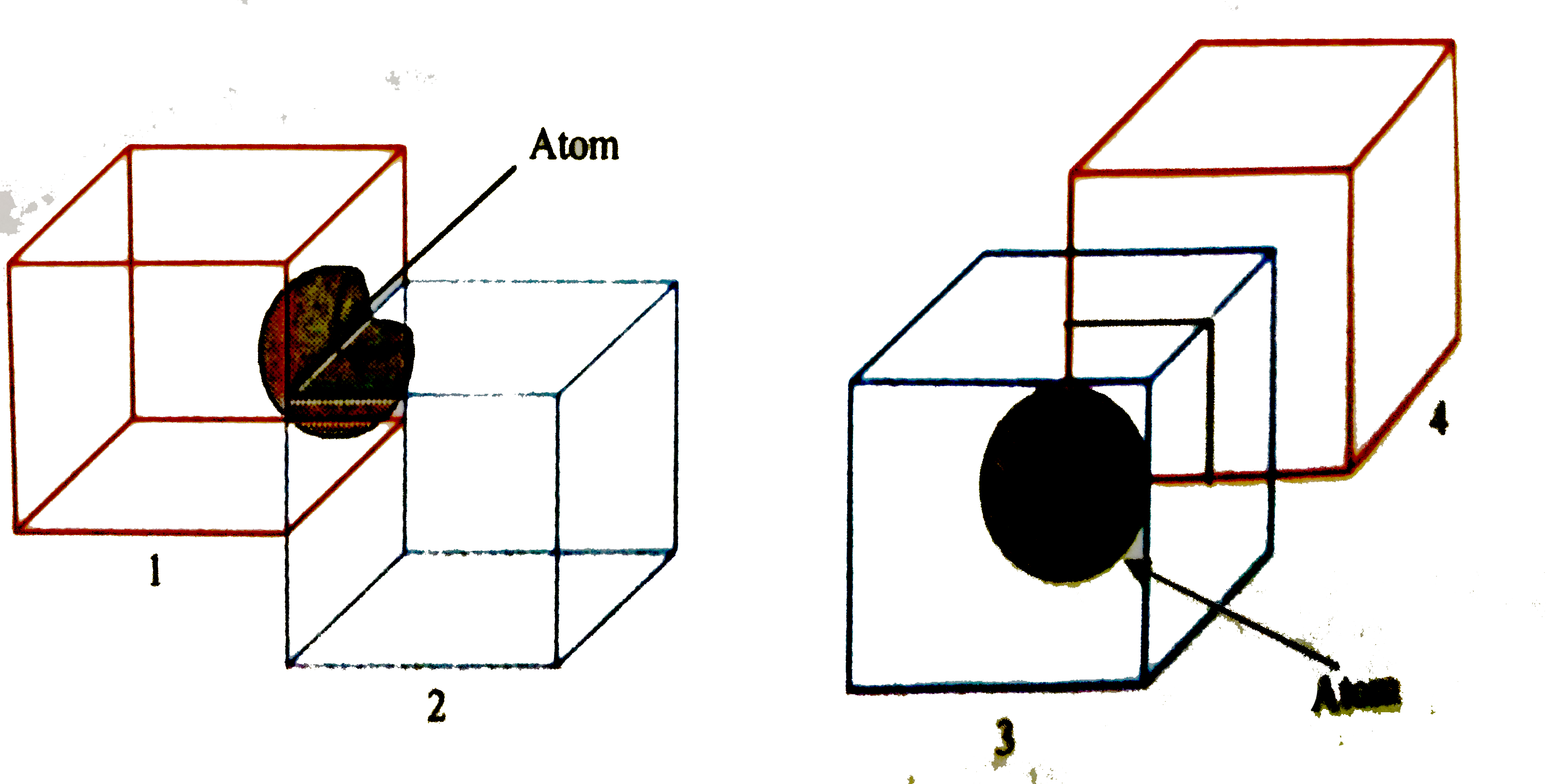 A12,14,1,18B12,14,18,1C18,14,1,12D18,14,12,1
A12,14,1,18B12,14,18,1C18,14,1,12D18,14,12,1Statements :
All spheres are cones
Some cubes are cones
All circles are cubes
Conclusions:
(i) No cube is sphere
(ii) All spheres may be cubes
(iii) Some cones are not circles
(iv) At least some cubes are circles
(v) Some cones which are cubes may be circlesA(i) & (ii) does not followB(i) & (iii) does not followC(ii)& (v) does not followD(iii) & (iv) does not follow

