Arithmetic mean of a continuous frequency distribution
Arithmetic Mean
Here we will become familiar with all the Arithmetic Mean Formula With Example. The arithmetic mean is characterized as the sum of all item values divided by the total number of items. The arithmetic mean is also known as the arithmetic average. It is the most common method used to measure the central tendency.
Simple Arithmetic Mean/Average
Here we will look at the method to find simple number arithmetic mean for continuous series.
Continuous Series
Simple Arithmetic mean (X)=∑fm/N
N=∑f
N = sum of the frequencies, i.e., ∑f
∑fm = sum of the product of middle values and their respective frequencies
Representation of information in a tabular or graphical form which indicates the frequency (number of times an observation occurs inside a specific range or interval) is known as a frequency distribution.
On the off chance that the information is very large for instance, if we have to examine the marks of 500 students, at that point the representation of such information in an arbitrary fashion is not practical. So, we use the approach of 'Grouping of Data' based on class intervals..
In continuous frequency distribution, the class intervals are set in such a manner that there are no gaps between two intervals and each interval or class in the table has its corresponding frequency. The class intervals are arranged in such a manner that they must be totally unrelated and exhaustive.
One of the characteristics of some random frequency distribution is the central tendency. It is the characteristic by which the values of a variable will in general group around at the central value of the frequency distribution is called central tendency.
An average value which is used to represent the entire series should neither have the lowest value nor the highest value in the group, yet a value somewhere between two limits, possibly in the inside, where most of the items of the group cluster. As such an average is a represented estimation of the entire set of observations, e.g., when we say "Germans are taller than Japanese" we mean the average height of Germans is more than the average height of Japanese people. Sometimes a measure of central tendency is known as a measure of a location because it indicates the location of the frequency distribution along the variable axis.
Some standard measures of central tendency are:
1. Arithmetic Mean
2. Geometric Mean
3. Harmonic Mean
4. Median
5. Mode
Arithmetic mean:
The Arithmetic mean of a pool of data is characterized to be the sum of the all number of observations of the data pool or set divided by the total number of observations.
On the off chance that be the values assumed by a variable, at that point their number arithmetic mean or A.M. is characterized as:
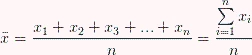
Example: The weights of 5 persons are 67 Kg, 60 Kg, 70 Kg, 57 Kg and 41 Kg. Calculate the arithmetic mean of weights.
Solution:
According to the definition of A.M.:
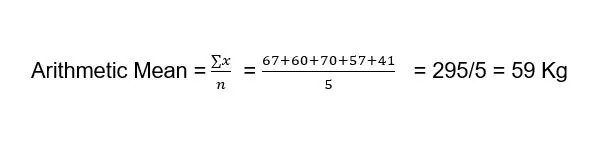
For frequency distribution data (discrete or continuous), if x1, x2, x3….xn be the values assumed by a variable ‘x’ with corresponding frequencies f1, f2, f3…. fn such that 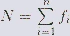 , then the arithmetic mean will be:
, then the arithmetic mean will be:

In the event that there are class intervals, at that point we discover the class mark or mid-estimation of each class stretch and treat it as the representative estimation of that specific class, i.e., we duplicate the class characteristic of each class with the frequency of that class and include these values.
In a sense, we are overlooking the class intervals by replacing them with respective class marks and in doing so we are changing over the grouped frequency distribution with class intervals into a simple frequency distribution with individual item values and respective frequencies in the place of class intervals.
Related Videos:
- Method to Calculate Mean by direct method
- Method to calculate Mean by short-cut method
- Method to calculate Mean by Step-Deviation method
- Arithmetic mean of a continuous frequency distribution
Let us look at an example below,
Example: Find the mean of the following frequency distribution
Class Intervals
Frequencies
Class Marks
20-30
10
25
30-40
20
35
40-50
25
45
50-60
15
55
60-70
20
65
70-80
10
75
Solution:
Class Intervals
Frequencies ( )
)
Class Marks ( )
)

20-30
10
25
250
30-40
20
35
700
40-50
25
45
1125
50-60
15
55
825
60-70
20
65
1300
70-80
10
75
750
Total
100
–
4950
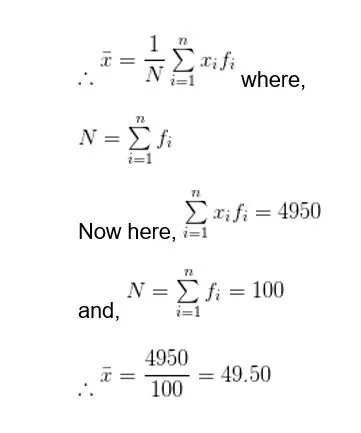
Applications of Arithmetic Mean:
Mean is used when:
1. Scores are almost symmetrically distributed around the main issue, i.e., distributions are not especially skewed.
2. We wish to know the central point of gravity of a sample.
3. The central tendency with the greatest stability is needed.
4. At the point when different statistics (standard deviation, coefficient of connection, ANOVA and ANCOVA, and so on.) for inferential purposes are to be determined.
5. Group performances are to be contrasted and exactness and precision.
6. At the point when scores are to be appropriately deciphered or when standard scores are to be registered.
7. When there are no extraordinary cases to influence the measure of central tendency.
8. When there are no class intervals of indefinite length.
9. At the point when further Arithmetical solution of the average is required.
Important Chapters:
N=∑f
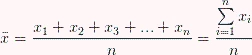
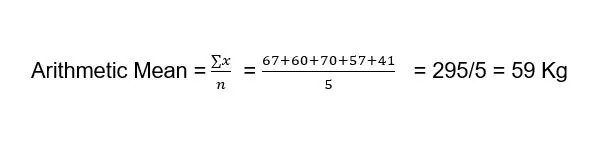
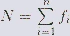 , then the arithmetic mean will be:
, then the arithmetic mean will be:
Class Intervals
Frequencies
Class Marks
20-30
10
25
30-40
20
35
40-50
25
45
50-60
15
55
60-70
20
65
70-80
10
75
Class Intervals
Frequencies ()
Class Marks ()
20-30
10
25
250
30-40
20
35
700
40-50
25
45
1125
50-60
15
55
825
60-70
20
65
1300
70-80
10
75
750
Total
100
–
4950
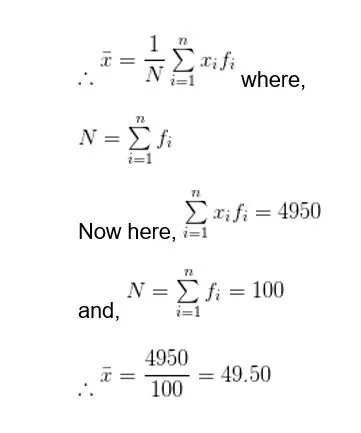
Similar Questions
Find the arithmetic mean of the following frequency distribution:

View SolutionThe arithmetic mean of the following frequency distribution is 53. Find the value of k.

View SolutionThe arithmetic mean of the following frequency distribution is 53. Find the value of k.

View SolutionCalculate the arithmetic mean of the following frequency distribution by Direct Method:
Class Interval10−2020−4040−7070−120120−200Frequency 4 10 26 8 2
View SolutionCalculate the arithmetic mean of the following frequency distribution by Direct Method:
Class Interval10−2020−4040−7070−120120−200Frequency 4 10 26 8 2
View SolutionFind the mean deviation about arithmetic mean of the following frequency distribution.Marks 0−10,10−20,20−30,30−40,40−50 No. of Students 5,8,15,16,6
View SolutionComputation of mode for a continuous frequency distribution - Method
View SolutionThe arithmetic mean of the following frequency distibution is 25. Determine the value of p.

View SolutionFind arithmetic mean from following frequency distribution

View SolutionFind the mode of following continuous frequency distribution
View Solution

