Division algorithm for polynomials
Division Algorithm for Polynomials
In Mathematics, arithmetic operations like addition, subtraction, division and multiplication plays a major role. Even in day to day life routine, we make use of these arithmetic operations. It is to be noted that except the division operation, all other operations go easy with the polynomials. Here, it becomes quite complex. But in this chapter, we will discuss the division algorithm for polynomial. We will also try to have a look at some examples that would prove to be of much help to understand it better.
What is the Division of Polynomial ?
When there is an involvement of any two polynomials, it is known as the polynomial division. When it comes to the division of polynomials, it can occur between a polynomial and a monomial, two monomials or even between two polynomials. Before discussing the procedure of dividing polynomials, we will have a good look at the brief introduction to polynomials.
Polynomial:
The algebraic expression of the type anxn + an−1xn−1+…………………a2x2 + a1x + a0, where “n” is either 0 or positive variables and real coefficients is considered to be a polynomial. Here, in this expression, we can find that the coefficients of the terms of the polynomial are an, an−1…..a1,a0
Look at the highest power of x in the above expression. Well, this is known as the degree of the polynomial.
A polynomial is represented by p(x) where x = k such that p(k) = 0. Well, in this case, k happens to be the root of the given polynomial.
Let us understand this with an example:
Example: Given a polynomial equation, p(x) = x2–x–2. Can you find the zeros of the equation?
Solution: Given,
The polynomial, p(x)=x2 – x – 2
Here the zeros of the equation is given by:
x2 – 2x + x – 2 = 0
x(x−2) + 1(x–2)
(x + 1)(x − 2) = 0
⇒ x = −1
Or, x = 2
Thus, -1 and 2 are zeros of the given polynomial.
Division of Polynomial
The process of splitting a quantity into equal amounts is known as Division of Polynomial. When it comes to mathematics, the process of repeated subtraction or the reverse operation of multiplication is termed as division. We can explain with an example. If we divide 20 by 4, the result we get is 5. Here, it can be understood that 4 got subtracted for 5 times from 20.
It is on algebraic expressions that the four basic operations viz. addition, subtraction, multiplication and division can be performed. We will now try to discuss the division of polynomials and algebraic expressions.
Types of Polynomial Division
When it comes to the division of polynomials, three cases can arise, which are as follows:
- Division of a monomial by another monomial
- Division of a polynomial by monomial
- Division of a polynomial by another polynomial
Now, to get a good understanding of the same, we will try to discuss all these cases one by one:
Division of a Monomial by Another Monomial
Let us consider the algebraic expression 40x2 and it needs to be divided by 10x then we get 40x2/10x = (2 × 2 × 5 × 2 × x × x)/(2 × 5 × x)
We can see that 2, 5 and x are found to be common in both the numerator and the denominator.
Therefore, 40x2/10x = 4x
Division of a Polynomial by Monomial
This is the second case when there is a division of a polynomial by monomial. To divide polynomials, there should be a division done separately for each term of the polynomial by the monomial. Here, to get the result, the quotient of each division needs to be added.
Division of Polynomial by Another Polynomial
In this case, when there is a need to divide a polynomial with another polynomial, the polynomial is needed to be written in standard form. This type of division is known as long division.
Related Videos:
- Types of polynomial
- Value of a polynomial
- Zeros or roots of polynomial
- Steps to draw a graph of a polynomial
- Graph of Linear polynomial
We will now try to work on some examples that can help in making the concept much easier.
Question 1: Solve: s2−4s = 5
Answer: Given s2−4s = 5
= s2−4s – 5 = 0
= (s + 1) (s - 5) = 0
= (s - 5) = 0
= s - 5 = 0
= s = 5
Or, (s + 1) = 0
s + 1 = 0
s = -1
Therefore, s = − 1 or s = 5.
Question 2: Solve: y2 – 5 = 7y/2 + 5/2
Answer: Given, y2 – 5 = 7y/2 + 5/2
= 2 (y2 – 5 = 7y/2 + 5/2)
= 2(y2) + 2(-5) = 2 (-7y/2) + 2 (5/2)
= 2 y2 – 10 = -7y + 5
= 2 y2 – 10 + 7y -5 = 0
= 2 y2 – 15 + 7y = 0
= 2 y2 + 7y – 15 = 0
Now, let us look at the table below to check whether this polynomials will be a factor.
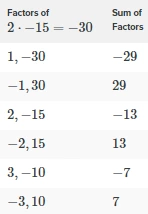
From the above table, we can see that the factors that will produce the middle term we want,−3, 10−3, 10. So, here, we need to place the factors in a way that will lead to a middle term of 7y7y:
Now (2y − 3)(y + 5)=0(2y − 3)(y + 5) = 0
Now we can set each factor equal to zero and solve:
(2y − 3)=0 OR (y + 5) = 0, 2y = 3 OR y = −5, y = 32 OR y = −5
Thus we have learned about division algorithm for polynomials where we have also attempted some questions.
Important Chapters:

Similar Questions
(RECAP)Relationship Between Zeroes And Ccofficients Of a polynomial|Division Algorithm For Polynomial
View Solution(RECAP)Relationship Between Zeroes And Ccofficients Of a polynomial|Division Algorithm For Polynomial
View SolutionDiscussion OF Exercise-2.2(Q.1 to 2) || Division algorithm OF polynomial || Remainder Theorem || Example based on division algorithm || Example and question || Discussion
View SolutionVerify division algorithm for the polynomials
p(x)=3x4−4x3−3x−1andg(x)=x−2.
Find p(2). What do you observe ?
View SolutionVerify division algorithm for the polynomials
p(x)=x3+x2+2x+3andg(x)=x+2.
Find p(−2). What do you observe ?
View SolutionVerify division algorithm for the polynomials f(x)=8+20x+x2−6x3 and g(x)=2+5x−3x2
View SolutionVerify the division algorithm for the polynomials p(x)=2x4−6x3+2x2−x+2andg(x)=x+2. p(x)=2x3−7x2+9x−13,g(x)=x−3.
View SolutionDivison Algorithm For Polynomials|Practice Problem|OMR
View SolutionDivision algorithm or Euclidean algorithm
View SolutionAlgorithm to factorize polynomials with integer coefficients (Step 1 to Step 7)
View Solution
