Question

Arrangement Of Raw Data (i) Alphabetical order (ii) Ascending order (iii) Descending order

Explanation

Primary and Secondary Data:

The data collected by an investigator herself or himself with a definite objective in her or his mind is called primary data.

When the information gathered from a source that already had the data stored, the retrieved data is called secondary data.

Raw Data

Let's consider the marks obtained in a mathematics test by ten students as given below

65 26 94 75 59 42 25 78 75 62

The data is called raw data in this form.

Range

The Data Range is called the difference between the lowest and highest values.

Range = Highest value – The lowest value

Ungrouped Frequency Distribution Table

Let’s find the marks (out of

100 marks) obtained by 30 class IX students of a school

 10 20 36 93 96 40 50 56 60 70

 93 89 80 70 72 70 34 40 36 40

 93 40 50 50 56 60 70 60 60 89

To make the data more understandable, we write it in the table below

Marks	Number of students (i.e., the frequency)
10	1
20	1
36	2
40	4
50	3
56	2
60	4
72	1
80	1
89	2
93	3
96	1
Total	25

This table is called a table of ungrouped frequency distribution, or only a table of the distribution of frequencies. When planning specific tables, we can use tally points.

The number of students that got a certain amount of marks is called the frequency of those marks. In the above data, four students received 60 points. So 60 mark frequency is 4.

Grouped Frequency Distribution Table

Let's take the following example of gathering data.

During Van Mahotsava 100 plants were planted each in 100 schools. The number of plants which survived after one month was recorded as

 95 66 28 32 65 65 69 34 98 96

 76 45 32 38 42 40 40 69 94 92

 75 84 76 83 85 62 37 65 63 42

 89 65 72 81 49 52 64 76 83 92

 93 68 52 79 82 83 59 82 75 82

 84 90 44 62 31 36 38 42 39 83

 87 56 58 24 35 76 82 85 30 68

 69 86 86 43 45 39 83 75 66 82

 92 74 89 66 91 27 88 89 90 42

 53 69 90 55 65 49 52 83 34 36

The above data may be condensed in a tabular form using tally marks as follows

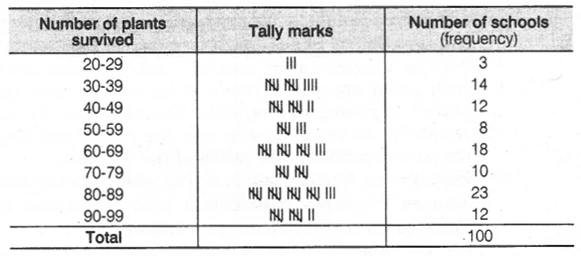
We condense it into groups, to represent such a large amount of data. These groupings are known as classes 20-29, 30-39.

The lower class limit is considered the least number in a class, and the highest number is regarded as the upper-class limit, as, in 20-29, 20 is lower, and 29 is the upper-class limit.

The class interval is called the difference between the lower and upper-class limits.

The midpoint of a class is known as the class mark. Thus,

Class mark= Upper class limit + Lower class limit / 2

Modified Table

The upper and lower differences Limits of 2 different classes in the frequency distribution graph. Thus, we need to split the intervals such that the upper and lower limits of successive intervals are the same for this we consider the discrepancy between the upper limit of a class and the lower limit of its successor class, Add half of that difference to each of the upper limits and remove from each of the lower limits the same.

 e.g., consider two consecutive classes 21-35 and 36-40.

 Then, difference = 36 – 35 = 1

 Half of the difference = 1 / 2 = 0.5

 So, the new class interval formed from 31-35 is 30.5-35.5 and from 36-40 is 35.5-40.5.

Graphical Data Representation

There is another type of data representation, a graphical representation of data. The principal graphic images are as follows

Bar graphs: A bar graph is a pictorial representation of data in which bars of uniform width are usually drawn with the same spacing between them on one axis (say the x-axis), representing the variable. The values of the variable are displayed at the other axis (say the y-axis), and the heights of the bars depend on the variable values.

Histogram: A graphical representation of a histogram is the continuous-class clustered frequency distribution. The building phases are as follows

We represent along the x-axis the class limits and frequencies along the y-axis on a suitable scale.

Now we draw rectangles (or rectangular bars) of width equal to the size of the class and lengths of the corresponding class intervals according to the frequencies.

Since no gaps exist between consecutive rectangles, the resulting graph appears as a solid figure. It is a histogram.

Remark:

If the interval of the first class does not start from zero, then we display it on the graph by labelling a kink or a break on the axis.

The area of the erected rectangles in a histogram is proportional to the respective frequencies.

If the widths of the rectangles differ, we need to make some adjustments in the lengths of the boxes So that the frequencies are again proportional to the areas. The measures to take in this regard are as set out below

Choose an interval with a minimum size of the class.

Then, rectangle lengths are adjusted to the size corresponding to the minimum class. Those lengths are called 'Lengths proportional to the size of the minimum class.'

Note: If both histogram and polygon frequency are drawn, then drawing a histogram first, and then a polygon frequency is advisable.

Related Videos:

• Why statistics?


• Statistics in plural sense


• Presentation Of Data


• Ungrouped Data


• Frequency Distribution

Mean

The mean (or average) observations is the sum of the values of all the observations divided by the total number of observations. Thus,

Combined mean

If the mean of n1 observations is X₁  and the mean

of n2 observations is X₂  then the combined mean of these observations is

x₁₂ = x₁n₁ + x₂n₂ / n₁n₂

Median

The median is the number of observations given, which divides it into exactly two parts. Thus, the median is the middle-most score.

To Find Median: The data arranged in ascending first of all (or descending) order. Then, the median of the ungrouped data calculates as follows

(i) If the number of observations (n) is odd, the mean value of the observation that shall be n+1 / 2

(ii) The mean of n / 2 the observations is the median if the number of observations (n) is even.

Mode

The mode is the observation value, which most frequently occurs, i.e., the model is called an observation with the maximum frequency.

Extreme values affect the mean in the data. The absolute values present in the data don't change the median and mode.

Important Chapters:

• NCERT Solution for Maths


• NCERT Solution for Maths Class 9 Statistics


• NCERT Solution for Maths Class 11 Statistics