Method of intial rates: Given the following data, determine the rate law expression and the value of the rate constant for the reaction. 2X+Y+Z→U+V

Strategy: The rate law is of the from
Rate=k[X]a[Y]b[Z]c
We must evaluate a,b,c, and k by using the reasoning outlined earlier. Thus, to determine order with respect to X, we must select those experiments in which concentration of X changes but the concentrations of Y and Z are kept onstant and so on. Note that the coefficient of U in the balenced equation is 1, so the rate of reaction is equal to the rate of formation of U.
Dependence on [Y] : In experiments 1 and 3, the intial concentrations of X and Z are unchanged. Thus, any change in the rate would be due to the change in concentration of Y. But we observethat the rate is the same in experiments 1 and 3, even though the concentration of Y is different. Thus, the reaction rate is independendent of [Y], thus b=0([Y]∘=1). The rate law must be
Rate=k[X]a[Z]c
We can neglet changes in [Y] in the subsequent reasoning. Dependence on [Z]: Experiments 1 and 4 involve the same initial concentration of X, thus the observed [Z]. Thus, we must compare experiments 1 and 4 to find Z. [Z] has been multiplied by a factor of 0.60M0.20M=3.0=[Z] ratio
Consequently, the rate changes by a factor of
7.2×10−6Ma−12.4×10−6Ms−1=3.0 = rate ratio
The exponent C can be reduced from
rate ratio =([Z]ratio)c
(3.0)=(3.0)c
thus c=1
i.e., the reaction is first order in Z. Now we know that the rate law is of the form .
Rate =k[X]a[Z]
Dependence on [X]: We use experiments 1 and 2 to evaluate a, because [X] is changed, [Y] does not matter, and [Z] is unaltered. The observed rate change is due only to changed [X]. [X] has been multiplied by a factor of
0.40M0.20M=2.0=[X] ratio
Consequently, the rate changes by a factor of
9.6×10−6Ms−12.4×10−6Ms(−1)=4.0 = rate ratio
The exponent a can be deduced from
rate ratio =([X]ratio)a
4.0=(2.0)a
(2.0)2=(2.)a
thus a=2
i.e., the reaction is second order in X
From these results, we can write the complete rate - law expression
Rate =k[X]2[Y]∘[Z]1
or Rate =k[X]2[Z]1
To evalute the specific reaction rate , k, we can substitute any of the four sets of data into the rate-law expression we have just derived. Data from experiment 4 give
Rate4=k[X]24[Z]4
k=Rate4[X]24[Z]4
=7.2x10−6Ms(−1)(0.20M)2(0.60M)
=300×10−6M−2s−1
=3.0×10−4M−2s−1
The rate-law expression can also be written with the value of k incorporated.
Rate=3.0×10−4M−2s−1[X]2[Z]
This expression allows us to calculate the reaction rate at which this reaction occurs with any known concentrations of X and Z (provided some Y is present).
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - R SHARMACHAPTER - CHEMICAL KINETICSEXERCISE - Follow-up 1
8 Videos
- CHEMICAL KINETICSBOOK - R SHARMACHAPTER - CHEMICAL KINETICSEXERCISE - Follow-up 2
10 Videos
- BIOMOLECULESBOOK - R SHARMACHAPTER - BIOMOLECULESEXERCISE - Archives
47 Videos
- CHEMISTRY IN EVERYDAY LIFEBOOK - R SHARMACHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - Archives
11 Videos
Similar Questions
Intitial rate method: Use the following initial rate data determine the form of the rate law expressoin for the reaction 3X+2Y→2U+V
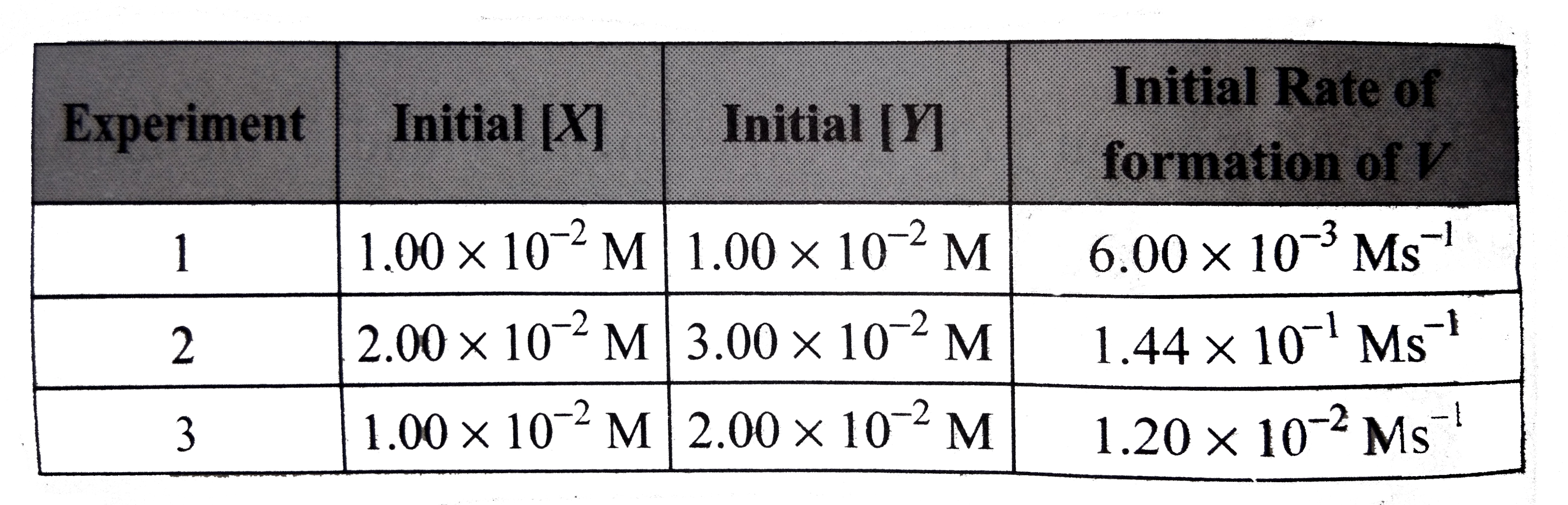
Strategy: The rate law is of the form
Rate=k[X]a[Y]b
No two experiments have the same in initial [Y], thus, use the alternative method discussed earlier to evalaute a and b.
View SolutionFor the given reaction, A+B→ Products following data were obtained
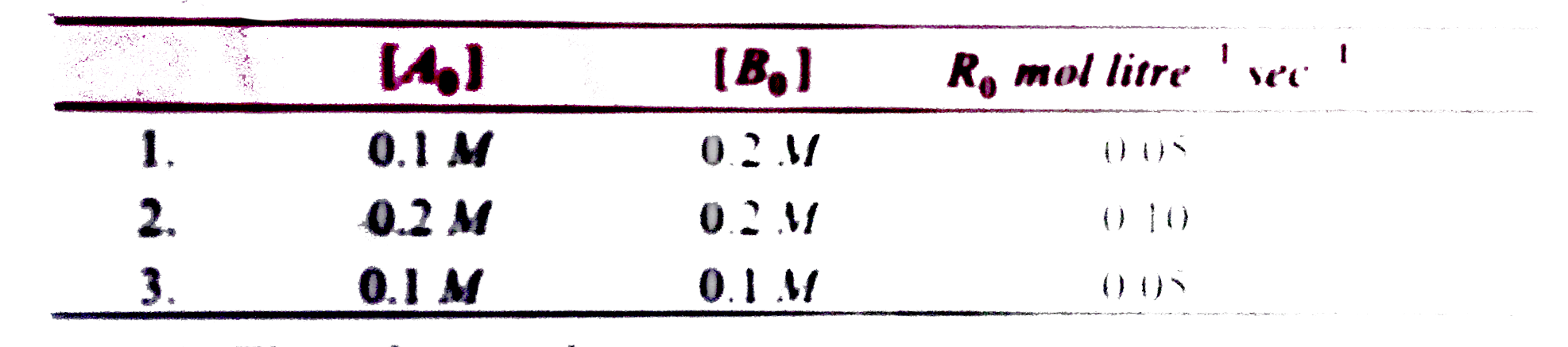
(i) Write the rate law expression.
(ii) Find the rate constant.
View Solution
Knowledge Check
In a reaction, the rate expression is Rate =k[A][B]2/3, the order of reaction is
A1B2C5/3DzeroFor a hypothetical reaction aA+bB→ Product, the rate law is: rate =K[A]x[B]y, then
A(a+b)=(x+y)B(a+b)<(x+y)C(a+b)>(x+y)DAll of theseForm the data given below for the reaction:A→B→ Products
the rate law expression is:ARate=k[A][B]BRate=k[A][B]2CRate=k[A]2[B]2DRate=k[A]2[B]
The data for the reaction A+B→C is
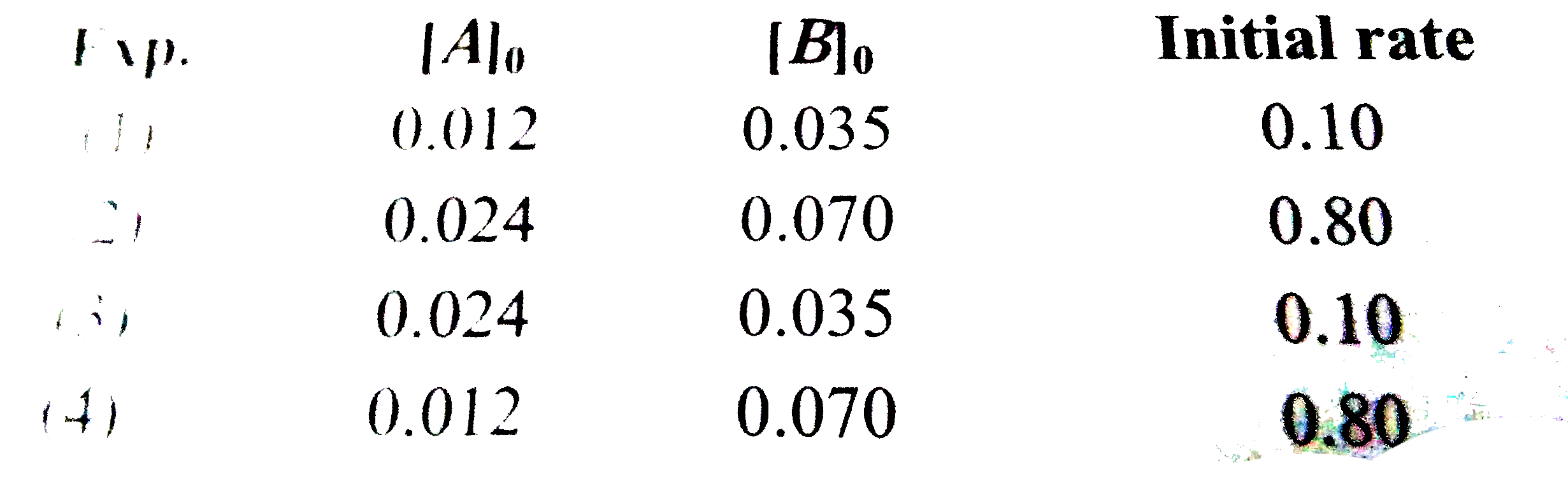
The rate law corresponds to the above data is
View SolutionThe rate of reaction X→Y becomes 8 times when the concentration of the reactant X is doubled. Write the rate law of the reaction.
View SolutionDerive an integrated rate law expression for first order reaction: A → B + C
View SolutionThe following initial rate data were obtained at 300K for the reactions:
2A+B→C+D

Deducethe rate law.
View SolutionFor a reaction ,A+B→C data is as follows :

the rate law for the reaction is
View Solution
