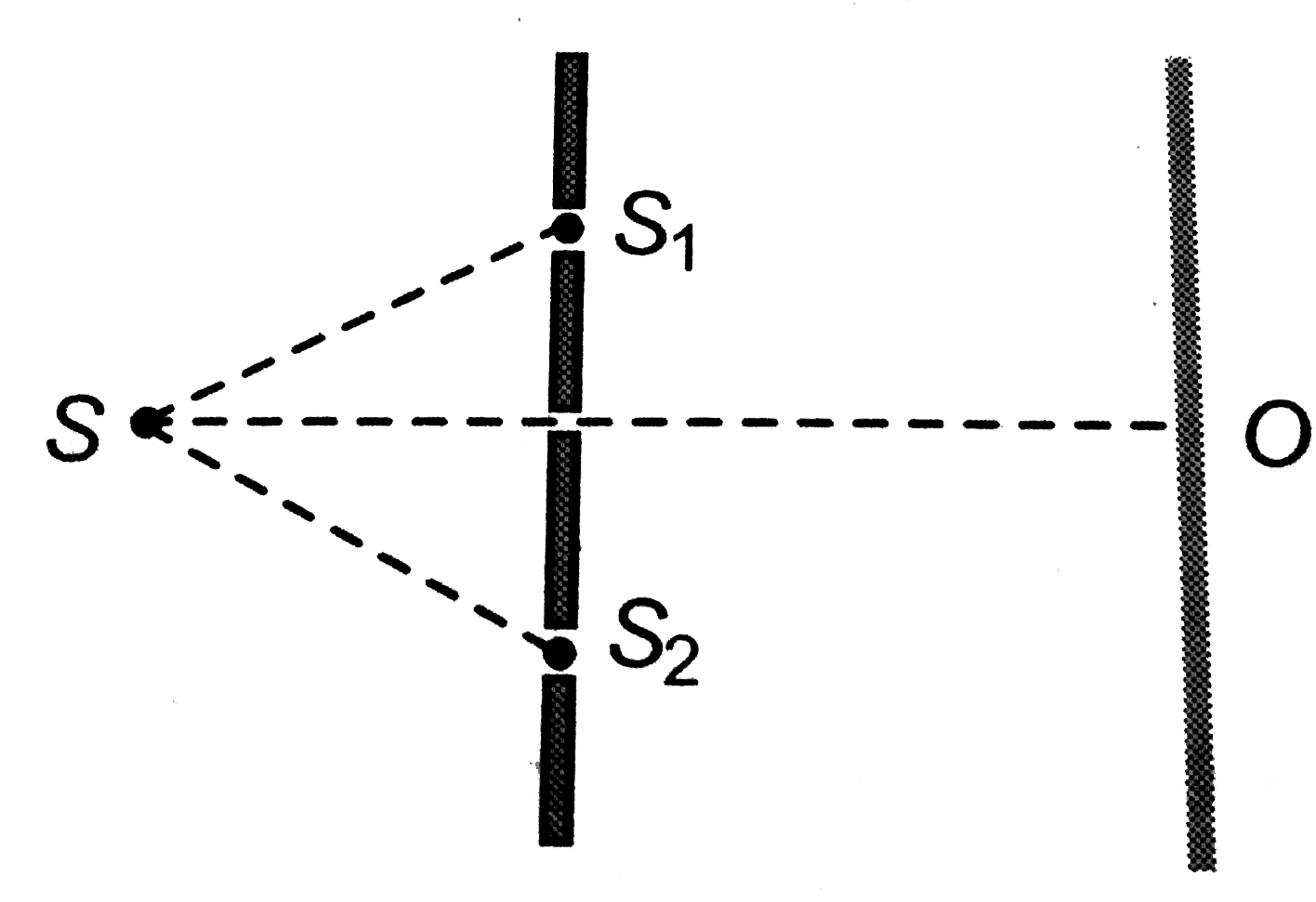
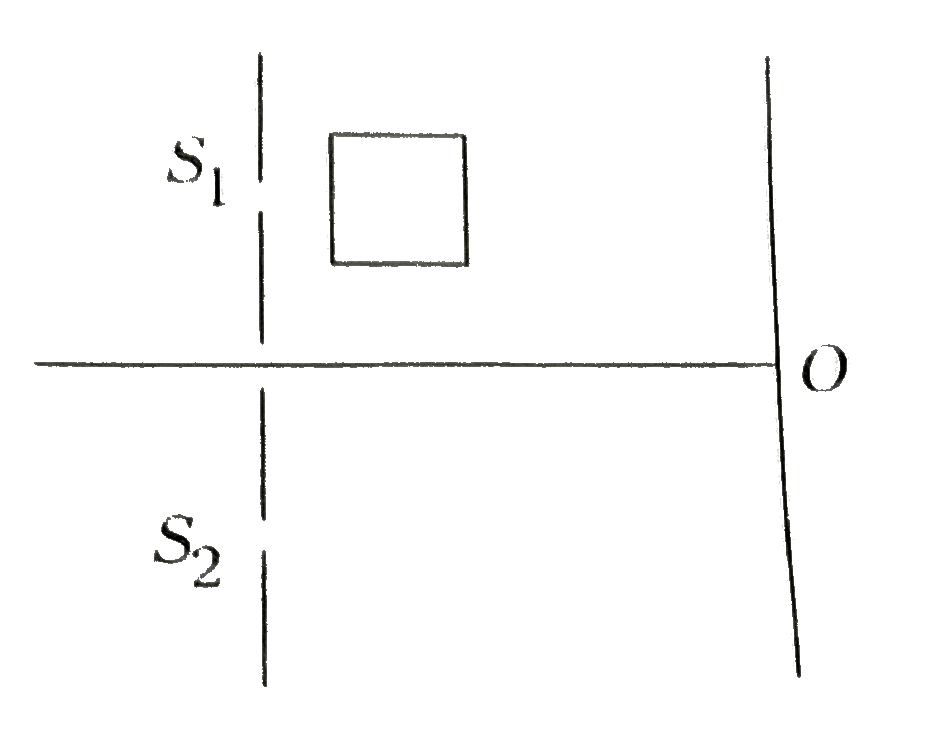
In the set up shown in figure, the two slits S1 and S2 are not equidistant from the slit S. The central fringe at O is then
always bright
always dark
either dark or bright depending on the position of S.
neither dark nor bright
The correct Answer is:C
Step by step video, text & image solution for In the set up shown in figure, the two slits S_1 and S_2 are not equidistant from the slit S. The central fringe at O is then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WAVE OPTICSBOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - LEVEL - I (C.W)
38 Videos
- WAVE OPTICSBOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - LEVEL - II (C.W)
31 Videos
- SEMICONDUCTOR ELECTRONICSBOOK - NARAYNACHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - ADDITIONAL EXERCISE (ASSERTION AND REASON TYPE QUESTIONS :)
19 Videos
Similar Questions
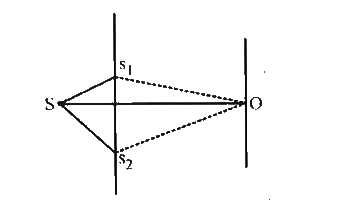
In an interference experiment, the two slits S1andS2 are not equidistant from the source S. then the central fringe at 0 will be
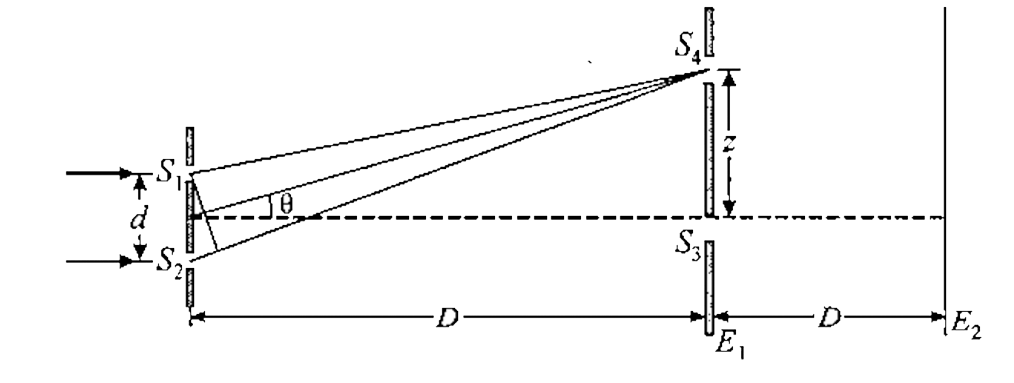
View SolutionConsider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d

View Solution
Knowledge Check
Consider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
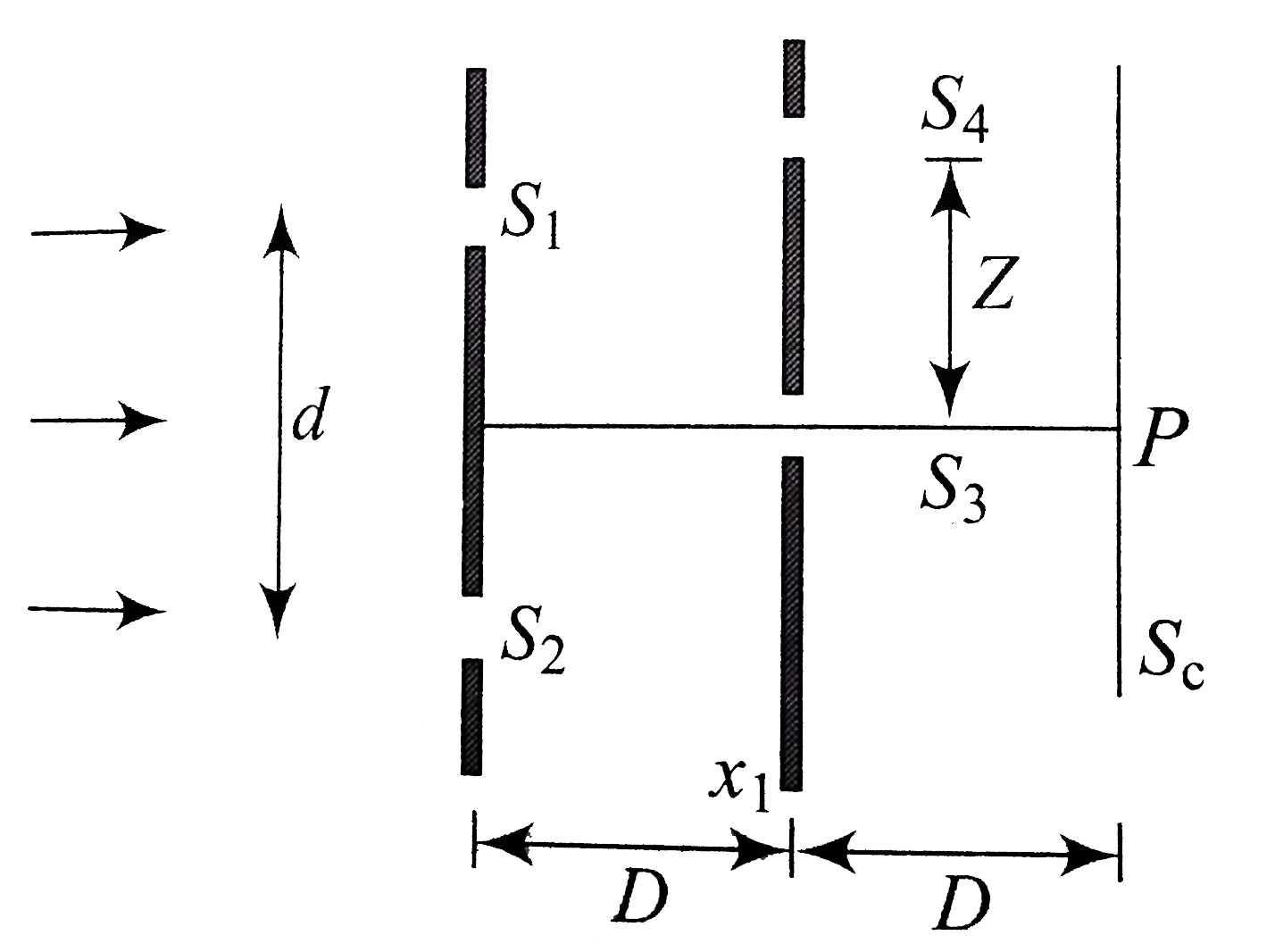
If z=λD2dA1B1/2C3/2D2Consider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
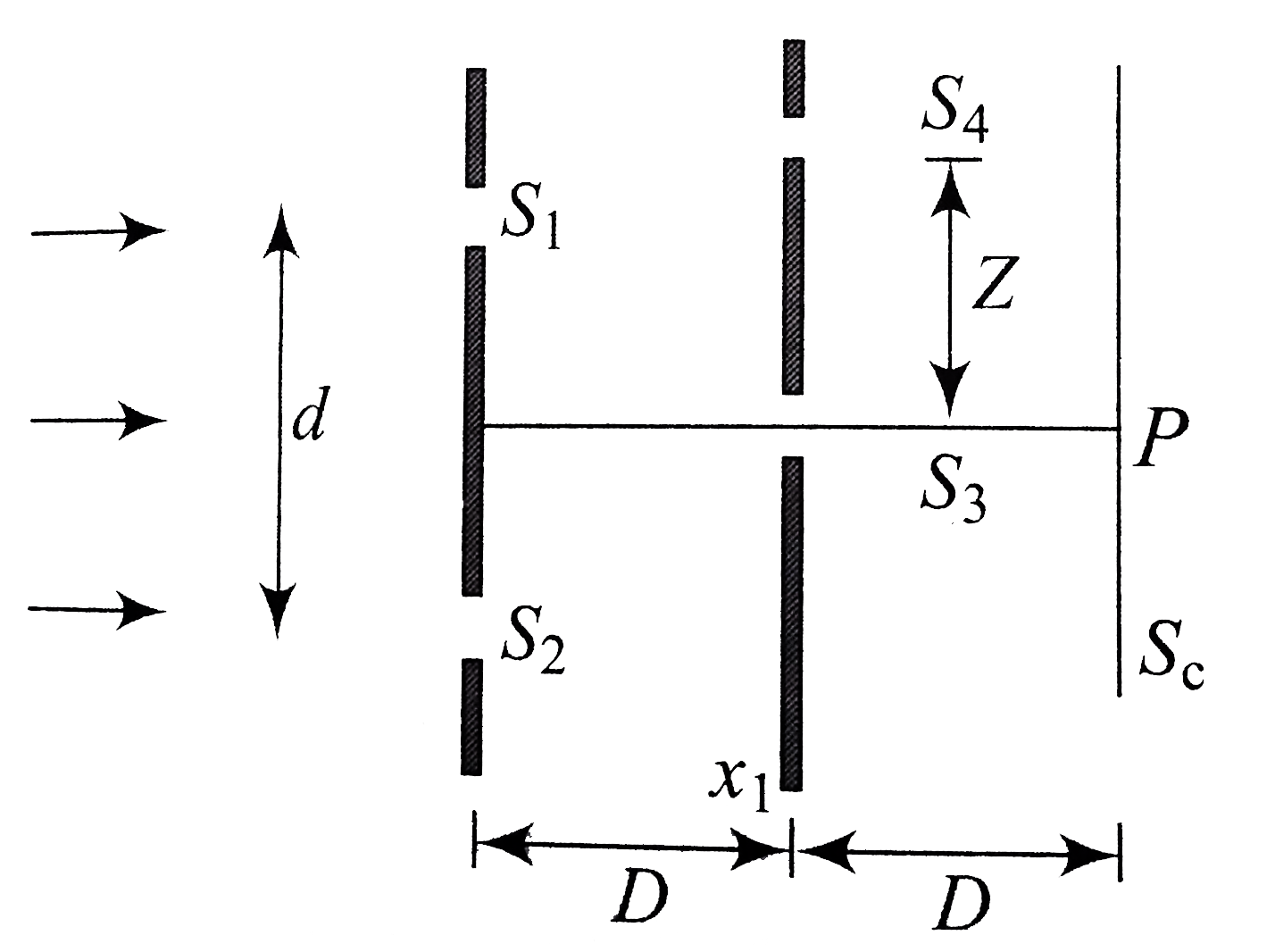
If z=λD4dA[3−2√2]2B[3+√2]2C[3−√2]2D[3+2√2]2Consider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
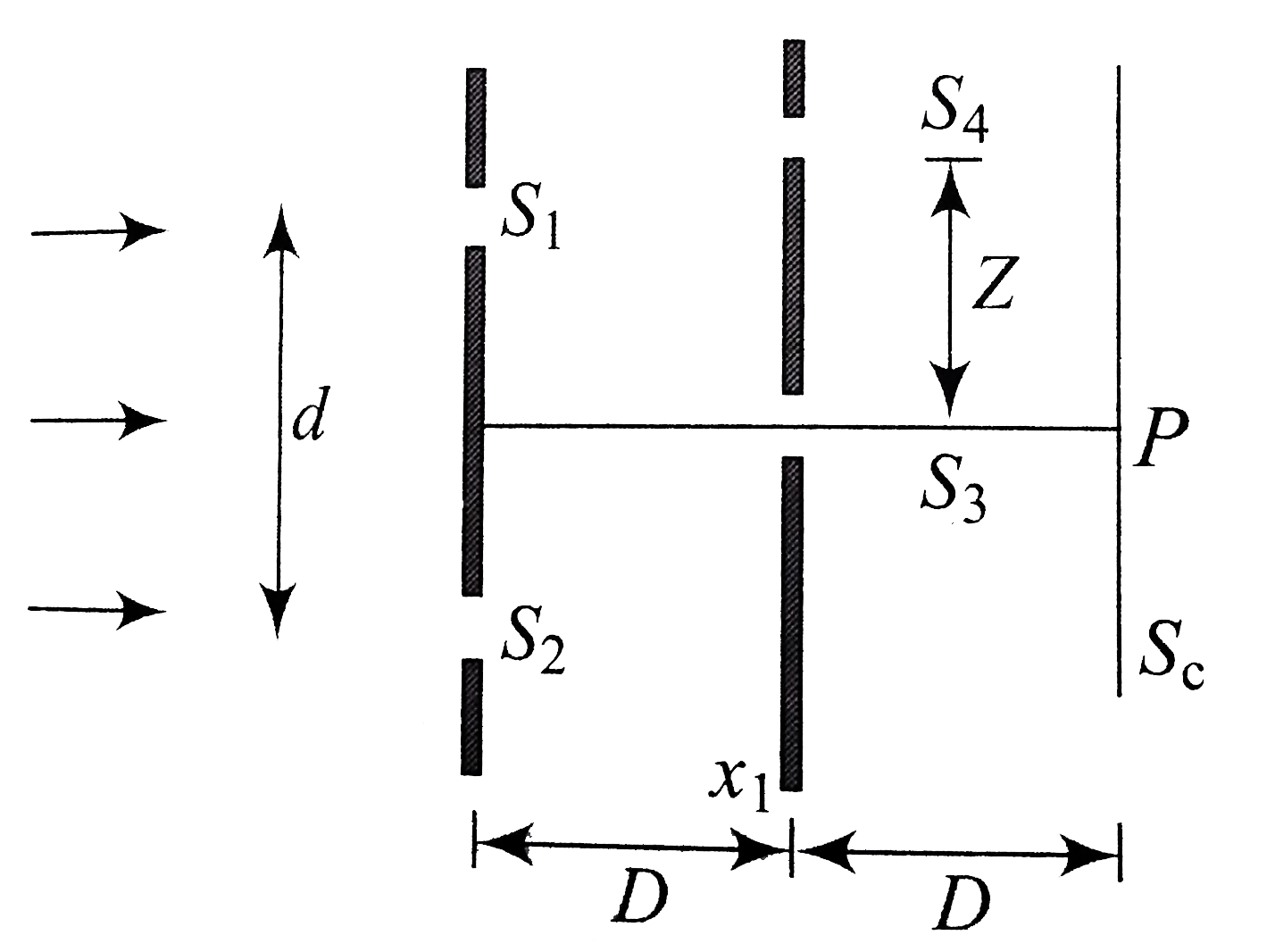
If z=λDdA4B2C∞D1
Consider the situation shown in figure-6.35. The two slits S1 and S2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen E1 placed at a distance D from the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3. Another screen E2 is placed a further distance D away from E1. Find the ratio of the maximum to minimum intensity observed on E2 if z is equal is : (a)λD2d (b)λDd (c)λD4d
View SolutionAssertion In the YDSE set up shown in figure a glass slab is inserted in front of the slit S1 as shown in figure Then zero order maxima (where path difference =0) will lie above point O.
Reason Glass slab will produce an extra path difference in the path of the ray passing through S1
View SolutionWhite coherent light (400nm−700nm) is sent through the slits of a Young's double slit experiment (as shown in the figure). The separation between the slits is 1mm and the screen is 100cm away from the slits. There is a hole in the screen at a point 1.5mm away (along the width of the fringes) from the central line. (a) For which wavelength (s) there will be minima at that point ? (b) which wavelength (s) will have a maximum intensity?

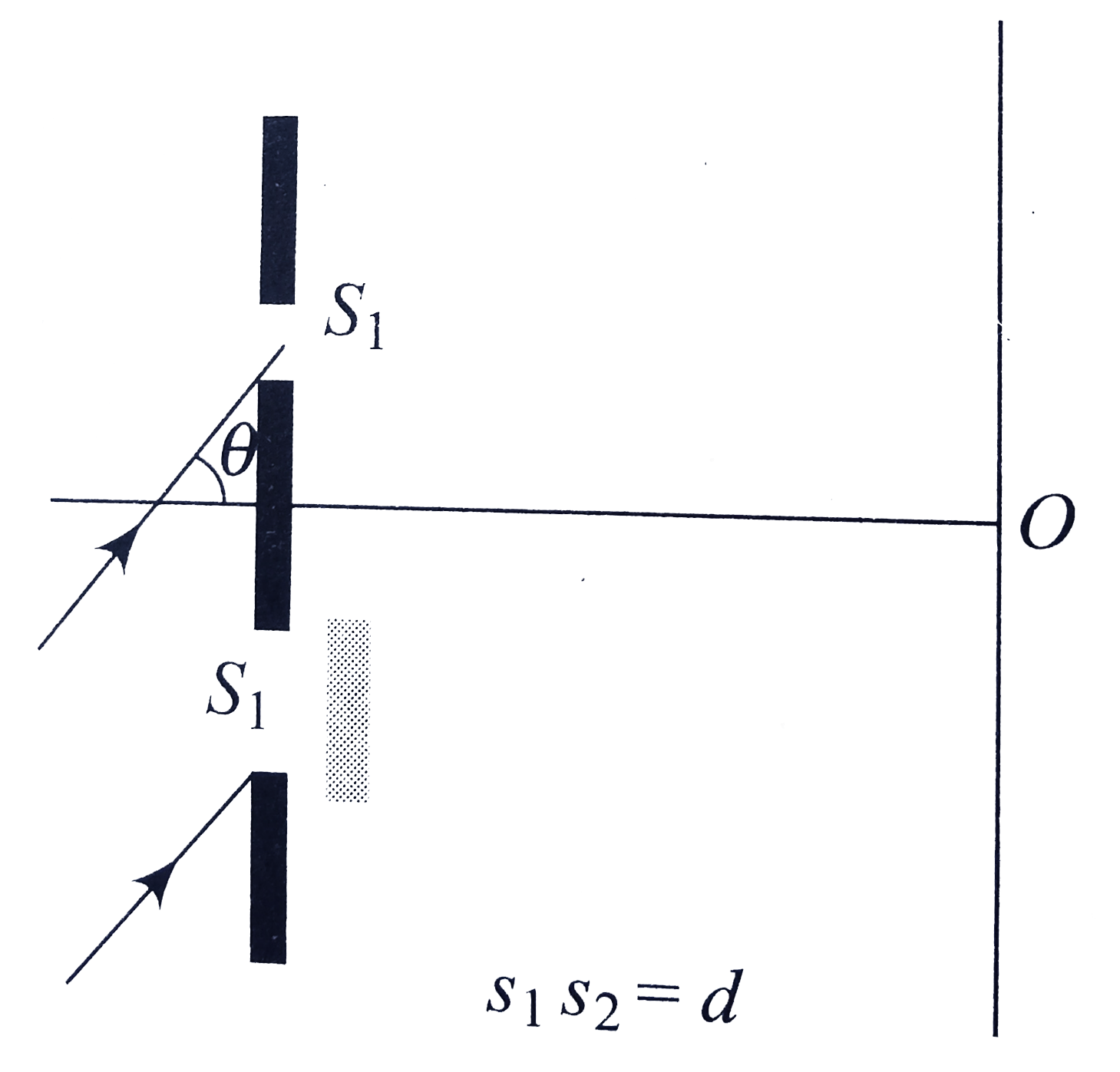
View SolutionA monochromatic beam of light fall on YDSE apparatus at some angle (say θ) as shown in figure. A thin sheet of glass is inserted in front of the lower slit s2. The central bright fringe (path difference =0) will be obtained
View SolutionIn Young’s experiment, monochromatic light through a single slit S is used to illuminate the two slits S1and S2. Interference fringes are obtained on a screen. The fringe width is found to be w. Now a thin sheet of mica (thickness t and refractive index μ) is placed near and in front of one of the two slits. Now the fringe width is found to be w’, then :
View Solution
