A magnet of length 10cm and magnetic moment 1Am2 is placed along the side of an equilateral triangle of the side AB of length 10cm. The magnetic induction at third vetex C is
10−9T
10−7
10−5T
10−4T
The correct Answer is:D
To find the magnetic induction at the third vertex C of an equilateral triangle formed by points A and B, where a magnet of length 10cm and magnetic moment 1Am2 is placed along side AB, we can follow these steps:
1. Identify the Given Data:
- Length of the magnet L=10cm=0.1m
- Magnetic moment M=1Am2
- Side length of the equilateral triangle AB=10cm=0.1m
2. Calculate the Pole Strength:
- The pole strength m can be calculated using the formula:
m=ML
- Substituting the values:
m=1Am20.1m=10A
3. Calculate the Magnetic Field at Point C Due to Pole A:
- The magnetic field BA at point C due to pole A is given by:
BA=μ04π⋅mr2
- Here, r=0.1m (distance from pole A to point C).
- The permeability of free space μ0=4π×10−7T m/A.
- Substituting the values:
BA=4π×10−74π⋅10(0.1)2=10−6⋅102=10−4T
4. Calculate the Magnetic Field at Point C Due to Pole B:
- The magnetic field BB at point C due to pole B is also:
BB=μ04π⋅mr2=10−4T
- Since both poles are equal in strength and distance from point C, BB is also 10−4T.
5. Determine the Resultant Magnetic Field at Point C:
- The angle between the two magnetic fields BA and BB is 120∘ (since they are at the vertices of an equilateral triangle).
- Using the formula for the resultant of two vectors:
Bresultant=√B2A+B2B+2BABBcos(120∘)
- Since BA=BB=10−4T:
Bresultant=√(10−4)2+(10−4)2+2(10−4)(10−4)(−0.5)
=√2×(10−4)2−(10−4)2=√(10−4)2=10−4T
6. Conclusion:
- The magnetic induction at point C is:
B=10−4T
- Length of the magnet L=10cm=0.1m
- Magnetic moment M=1Am2
- Side length of the equilateral triangle AB=10cm=0.1m
- The pole strength m can be calculated using the formula:
m=ML
- Substituting the values:
m=1Am20.1m=10A
- The magnetic field BA at point C due to pole A is given by:
BA=μ04π⋅mr2
- Here, r=0.1m (distance from pole A to point C).
- The permeability of free space μ0=4π×10−7T m/A.
- Substituting the values:
BA=4π×10−74π⋅10(0.1)2=10−6⋅102=10−4T
- The magnetic field BB at point C due to pole B is also:
BB=μ04π⋅mr2=10−4T
- Since both poles are equal in strength and distance from point C, BB is also 10−4T.
- The angle between the two magnetic fields BA and BB is 120∘ (since they are at the vertices of an equilateral triangle).
- Using the formula for the resultant of two vectors:
Bresultant=√B2A+B2B+2BABBcos(120∘)
- Since BA=BB=10−4T:
Bresultant=√(10−4)2+(10−4)2+2(10−4)(10−4)(−0.5)
=√2×(10−4)2−(10−4)2=√(10−4)2=10−4T
- The magnetic induction at point C is:
B=10−4T
Topper's Solved these Questions
- MAGNETISMBook:NARAYNAChapter:MAGNETISMExercise:LEVEL-II(C.W)
Explore 42 Videos
- MAGNETISMBook:NARAYNAChapter:MAGNETISMExercise:LEVEL-III(C.W)
Explore 30 Videos
- MAGNETISMBook:NARAYNAChapter:MAGNETISMExercise:C.U.Q (ASSERTION & REASON)
Explore 13 Videos
- EXPERIMENTAL PHYSICSBook:NARAYNAChapter:EXPERIMENTAL PHYSICSExercise:Comprehension type
Explore 6 Videos
- MAGNETISM AND MATTERBook:NARAYNAChapter:MAGNETISM AND MATTERExercise:EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
Explore 17 Videos
Similar Questions
Knowledge Check
Two short magnets of magnetic moment 1000Am2 are placed as shown at the corners of a square of side 10cm. The net magnetic induction at P is
 A0.1TB0.2TC0.3TD0.4T
A0.1TB0.2TC0.3TD0.4TA current of 2A is flowing in the sides of an equilateral triangle of side 9 cm. The magnetic field at the centroid of the triangle is
A1.66×10−6TB1.22×10−4TC1.33×10−6TD1.44×10−4TA magnet of megnetic moment 10 Am2 has magnetic length 5 cm.The strength of magnet is
A100 AmB200 AmC300 AmD400 Am
A current of 1A is flowing in the sides of equilateral triangle of side 4.5×10−2m. The magnetic induction at centroid of the triangle:
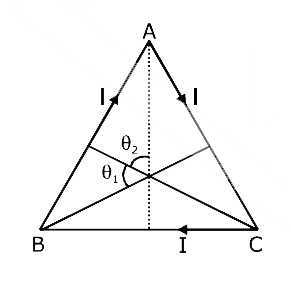
View SolutionFind the length of a altitude in on equilateral triangle of side 'a' cm
View SolutionFind the are of an equilateral triangle having each side of length 10 cm .
[Take√3=1.732.]
View SolutionConstruct an equilateral triangle, if one side is 10 cm.
View SolutionMagnetic field at center of an equilateral triangle of side length 9cm having current 2A is
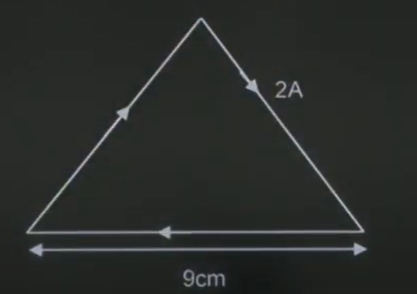
View Solution

