Two batteries of different emf and internal resistances connected in series with each other and with an external load resistor. The current reversed, the current becomes 1.0 A. the ratio of the emf of the two batteries is
2.5:1
2:1
3:2
1:1
The correct Answer is:B
To solve the problem, we need to analyze the situation with two batteries connected in series, each with different electromotive forces (emf) and internal resistances. We will derive the ratio of the emfs of the two batteries based on the information given about the currents.
1. Define Variables:
- Let e1 be the emf of the first battery.
- Let e2 be the emf of the second battery.
- Let r1 be the internal resistance of the first battery.
- Let r2 be the internal resistance of the second battery.
- Let R be the external load resistance.
2. Current in the Forward Direction:
- When the current is flowing in the forward direction, the total current I1 can be expressed as:
I1=e1+e2r1+r2+R
- According to the problem, I1=3A. Thus, we have:
3=e1+e2r1+r2+R(Equation 1)
3. Current in the Reversed Direction:
- When the current is reversed, the total current I2 can be expressed as:
I2=e1−e2r1+r2+R
- According to the problem, I2=1A. Thus, we have:
1=e1−e2r1+r2+R(Equation 2)
4. Forming the Ratio:
- Now, we will divide Equation 1 by Equation 2 to eliminate the common denominator:
31=e1+e2e1−e2
- This simplifies to:
3(e1−e2)=e1+e2
- Rearranging gives:
3e1−3e2=e1+e2
- Combining like terms leads to:
3e1−e1=3e2+e2
2e1=4e2
5. Finding the Ratio:
- Rearranging gives:
e1e2=42=2
Conclusion:
The ratio of the emf of the two batteries is:
e1e2=2
- Let e1 be the emf of the first battery.
- Let e2 be the emf of the second battery.
- Let r1 be the internal resistance of the first battery.
- Let r2 be the internal resistance of the second battery.
- Let R be the external load resistance.
- When the current is flowing in the forward direction, the total current I1 can be expressed as:
I1=e1+e2r1+r2+R
- According to the problem, I1=3A. Thus, we have:
3=e1+e2r1+r2+R(Equation 1)
- When the current is reversed, the total current I2 can be expressed as:
I2=e1−e2r1+r2+R
- According to the problem, I2=1A. Thus, we have:
1=e1−e2r1+r2+R(Equation 2)
- Now, we will divide Equation 1 by Equation 2 to eliminate the common denominator:
31=e1+e2e1−e2
- This simplifies to:
3(e1−e2)=e1+e2
- Rearranging gives:
3e1−3e2=e1+e2
- Combining like terms leads to:
3e1−e1=3e2+e2
2e1=4e2
- Rearranging gives:
e1e2=42=2
The ratio of the emf of the two batteries is:
e1e2=2
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:NARAYNAChapter:CURRENT ELECTRICITYExercise:Level 3
Explore 46 Videos
- CURRENT ELECTRICITYBook:NARAYNAChapter:CURRENT ELECTRICITYExercise:NCERT Based Questions
Explore 13 Videos
- CURRENT ELECTRICITYBook:NARAYNAChapter:CURRENT ELECTRICITYExercise:Level 2 C.W
Explore 59 Videos
- COMMUNICATION SYSTEMBook:NARAYNAChapter:COMMUNICATION SYSTEMExercise:Level-II(H.W)
Explore 25 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:NARAYNAChapter:DUAL NATURE OF RADIATION AND MATTERExercise:ASSERTION AND REASON
Explore 15 Videos
Similar Questions
Two batteries of different emfs and different internal resistances are connected as shown. The voltage across AB in volts is.
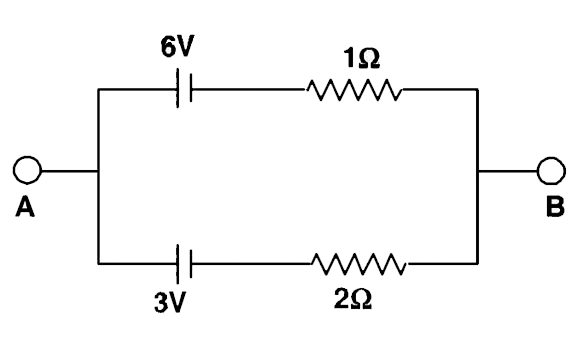 .
.
View SolutionA cell of emf ε and internal resistance (r) is connected in series with an external resistance (nr) then the ratio of the terminal potential difference to emf is:
View Solution
Knowledge Check
Two batteries of difference emf's and internal resistance are connected in parallel to one another.
AEquivalent emf will be grater than either of the emf'sBEquivalent emf will be smaller than either of the emfCEquivalent internal resistance will be grater than either of the two internal resistancesDEquivalent internal resistance will be smaller than either of the two internal resistances.Four cells, each of emf E and internal resistance r, are connected in series across an external resistance reverse. Then, the current in the external circuit is
A2E4r+RB3E4r+RC3E3r+RD2E3r+RN batteries each of emf E and internal resistance r are first connected in series and then in parallel to an external resistance R. if current through R is same in both cases then.
AR=r2/NBR−Nr/2CR=NrDR=r
Three cells each of emf 1.5 V, after being connected in series with each other, are connected to the ends of a resistance. The current obtained is 1 A. When the cells are connected in parallel across the ends of the same resistance, the current is found to be 0.36 A. Find the external resistance and the internal resistance of each cell.
View SolutionA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
View SolutionTwo batteries each of E and internal resistance r are connected turn by turn in series and in parallel, and are used to find current in an external resistance R. If the current in series is equal to that in parallel, the internal resistance of each battery is
View SolutionA battery of emf 15 V and internal resistance of 4Ω is connected to a resistor. If the current in the circuit is 2A and the circuit is closed. Resistance of the resistor and terminal voltage of the battery will be
View SolutionA battery of emf 10 V and internal resistance 3Ωis connected to a resistor. The current in the circuit is 0.5 A . The terminal voltage of the battery when the circuit is closed is
View Solution

