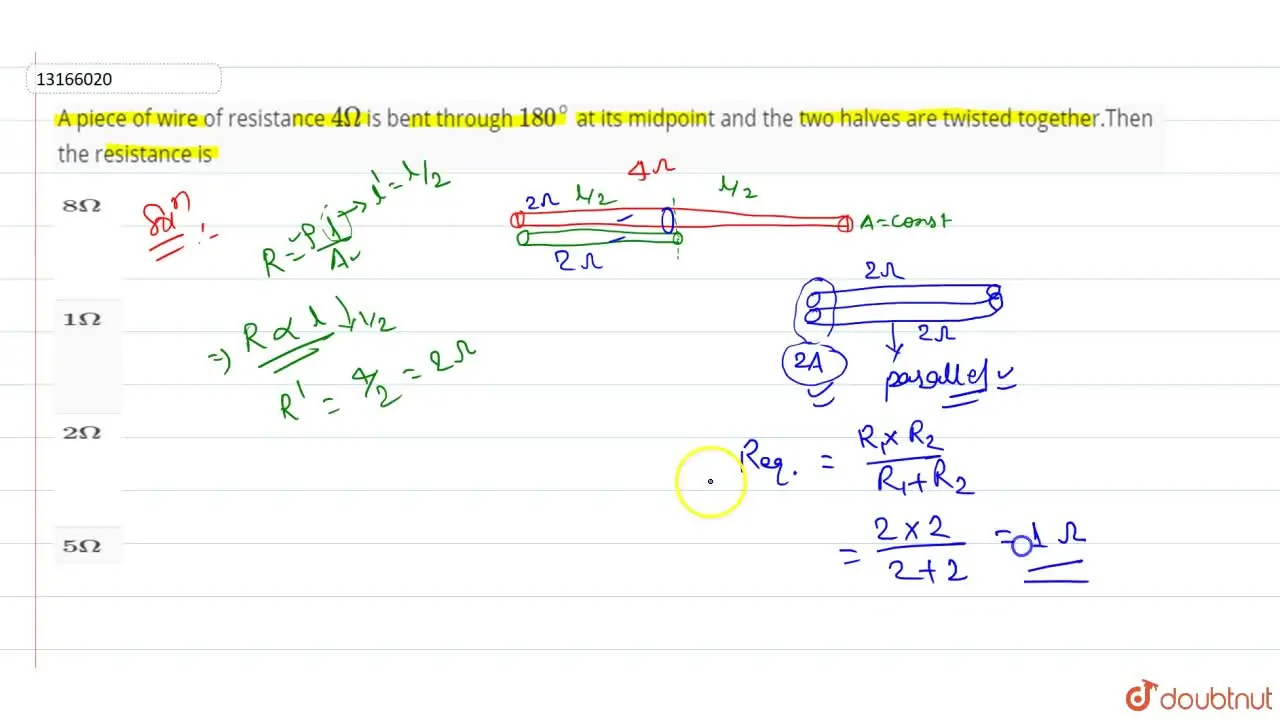
A piece of wire of resistance is bent through at its midpoint and the two halves are twisted together.Then the resistance is
The correct Answer is:B
Related Playlists
- BOOK - NARAYNACHAPTER - CURRENT ELECTRICITYEXERCISE - Level 1 H.W63videos
CURRENT ELECTRICITY
- BOOK - NARAYNACHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 C.W59videos
CURRENT ELECTRICITY
- BOOK - NARAYNACHAPTER - CURRENT ELECTRICITYEXERCISE - C.U.Q105videos
CURRENT ELECTRICITY
- BOOK - NARAYNACHAPTER - COMMUNICATION SYSTEMEXERCISE - Level-II(H.W)25videos
COMMUNICATION SYSTEM
- BOOK - NARAYNACHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - ASSERTION AND REASON15videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
A piece of wire of resistance 4 ohm s is bent through 180∘ at its mid point and the two halves are twisted together, then the resistance is
View SolutionA8Ω resistance wire is bent through 180∘ at its mid point and the two halves are twisted together. Then the resistance is
View SolutionA piece of wire of resistance 20Ω is drawn out so that its length is increased to twice its original length. Calculate the resistance of the wire in the new situation.
View Solution(a) State four factors on which the resistance of a conductor depends.
(b) A piece of wire of resistance 20 Ω is drawn out so that its length is increased to twice its original length. Calculate the resistance of the wire in the new situation.View SolutionA 4Ω non insulated resistance wire is bent in the middle by 180∘ and both the halves are twisted with each other. What will be its new resistance ?
View SolutionA piece of wire of resistance 20Ω is drawn so that its length is increased to twice is original length. Calculate resistance of the wire in the new situation.
View SolutionA wire of resistance (1 Ω) is divided into two halves and both halves are connected in parallel. Find the new resistance.
View SolutionA wire of resistance 2Ω is stretched so that its radius is halved. Determine its new resistance.
View SolutionThe resistance of a wire is R. It is bent at the middle by 180∘ and both the ends are twisted together to make a shorter wire. The resistance of the new wire is
View SolutionA wire of resistance 5Ω is bent in the form of a closed circle. Find the resistance across the diameter of the circle.
View Solution