n identical calls, each of internal resistance (r) are first connected in parallel and then connected in series across a resistance (R). If the current through R is the same in both cases, then
R=r2
r=R2
R=r
r=0
The correct Answer is:C
Step by step video, text & image solution for n identical calls, each of internal resistance (r) are first connected in parallel and then connected in series across a resistance (R). If the current through R is the same in both cases, then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CURRENT ELECTRICITYBook:NARAYNAChapter:CURRENT ELECTRICITYExercise:Level 1 C.W
Explore 64 Videos
- CURRENT ELECTRICITYBook:NARAYNAChapter:CURRENT ELECTRICITYExercise:Level 1 H.W
Explore 63 Videos
- CURRENT ELECTRICITYBook:NARAYNAChapter:CURRENT ELECTRICITYExercise:Level 6
Explore 43 Videos
- COMMUNICATION SYSTEMBook:NARAYNAChapter:COMMUNICATION SYSTEMExercise:Level-II(H.W)
Explore 25 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:NARAYNAChapter:DUAL NATURE OF RADIATION AND MATTERExercise:ASSERTION AND REASON
Explore 15 Videos
Similar Questions
Two identical cells, each of emf ε , having negligible internal resistance, are connected in parallel with each other across an external resistance R. What is the current through this resistance ?
View SolutionTwo identical cells each of emf ε, having negligible internal reistance r, are connercted in parallel with each other across an external resistance R. What is the current through this resistance.
View Solution
Knowledge Check
N batteries each of emf E and internal resistance r are first connected in series and then in parallel to an external resistance R. if current through R is same in both cases then.
AR=r2/NBR−Nr/2CR=NrDR=rn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
AnER+nrBnEnR+rCER+nrDnER+rFour cells, each of emf E and internal resistance r, are connected in series across an external resistance reverse. Then, the current in the external circuit is
A2E4r+RB3E4r+RC3E3r+RD2E3r+R
n-identical cells each of emf E and internal resistance r are connected in series. Find the expression for current in the circuit given below

View Solutionn identical cells, each of emf e volt and internal resistance rΩ are connected in a row m. Such rows are connected in parallel. This battery sends current through an external resistance R. The current will be maximum if
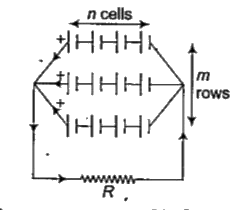
View Solutionn identical cells, each of emf e volt and internal resistance rΩ are connected in a row m. Such rows are connected in parallel. This battery sends current through an external resistance R. The current will be maximum if
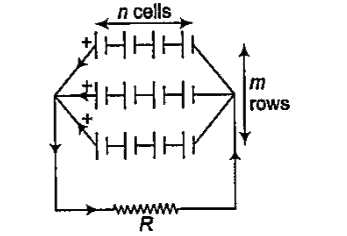
View SolutionTwo cells , each of emfE and internal resistance r, are connected in parallel across a resistor R. The power delivered to the resistor is maximum if R is equal to
View SolutionTwo batteries each of E and internal resistance r are connected turn by turn in series and in parallel, and are used to find current in an external resistance R. If the current in series is equal to that in parallel, the internal resistance of each battery is
View Solution

