A nucleus A (parent) decays into B (Daughter) with half life T1 and B decays into C with half life T2. Graph is drawn between number of atoms/activity versus time. Select the correct graph (s)
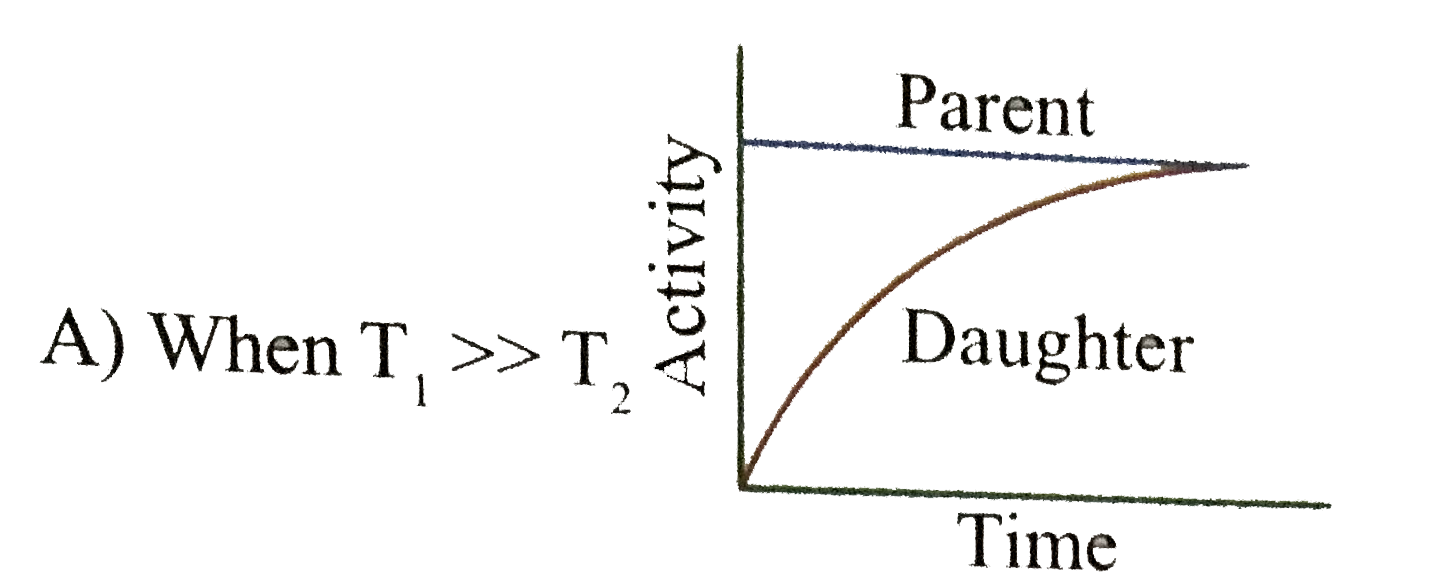

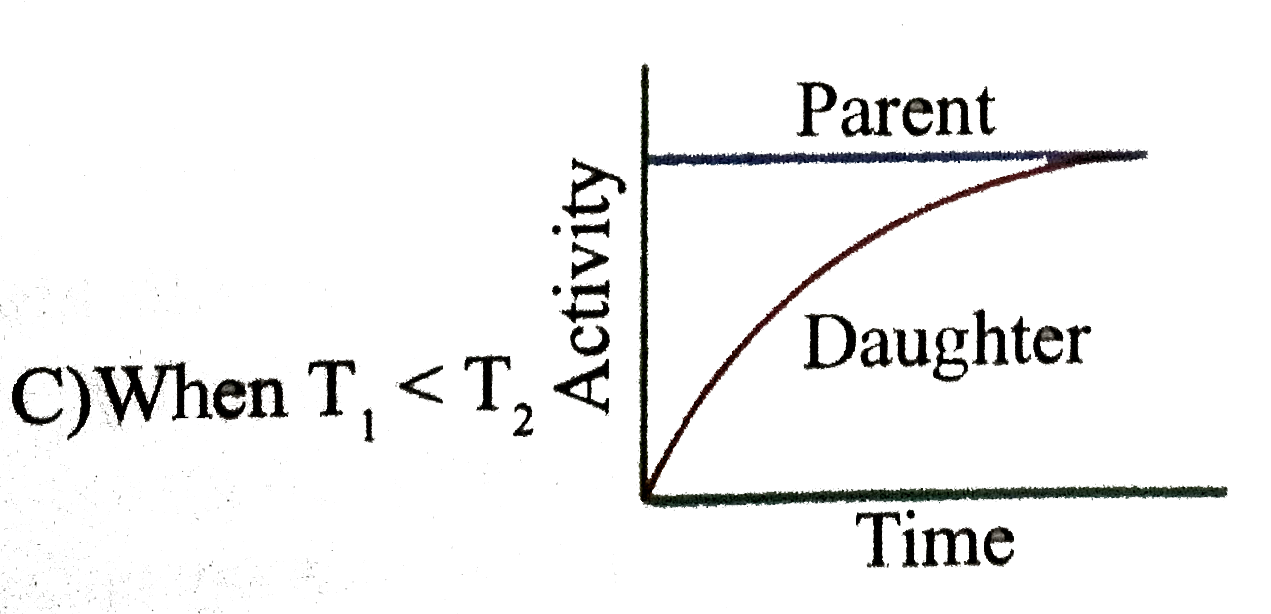

The correct Answer is:A, D
When T1>>T2, the no of nuclei of A (parent) almost when T1<T2, the no of nuclei of A (parent) decrease exponentially.
Topper's Solved these Questions
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - Previous JEE questions
21 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-I-(H.W)
16 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - Level-V Multiple answer questions
45 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE - 4
20 Videos
- NUCLEI BOOK - NARAYNACHAPTER - NUCLEI EXERCISE - ASSERTION & REASON
5 Videos
Similar Questions
Knowledge Check
The graph between number of decayed atoms N' of a radioactive element and time t is.
A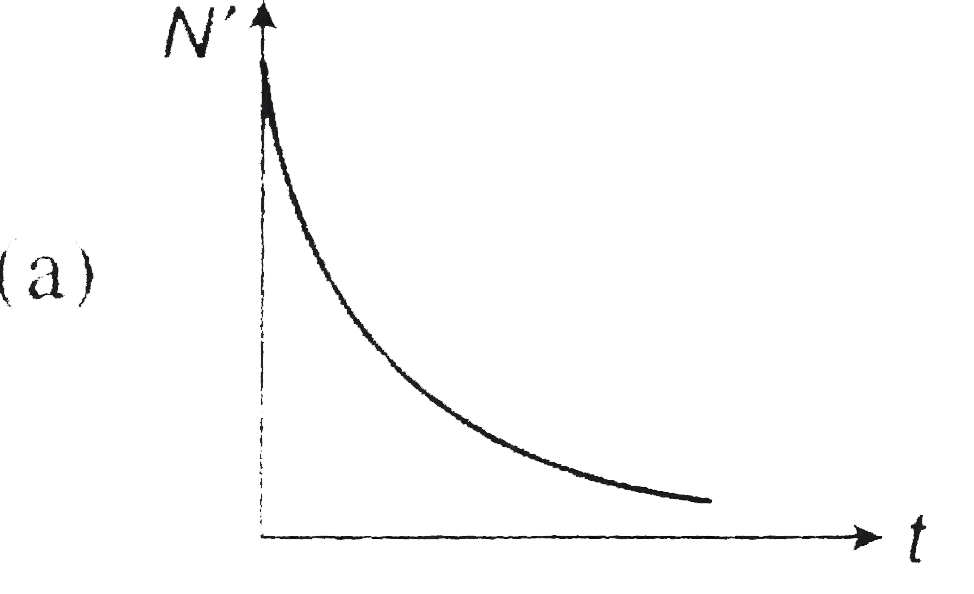 .B
.B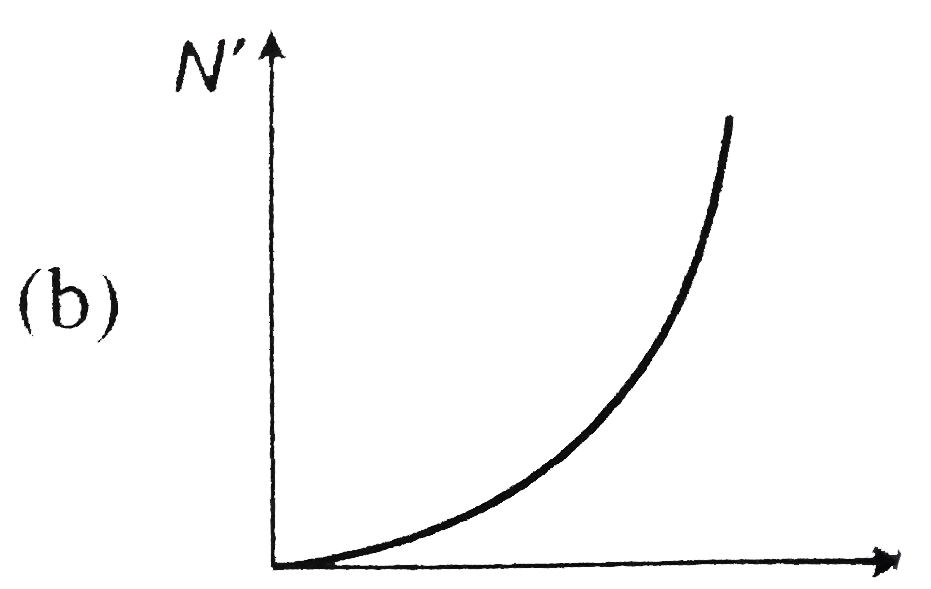 .C
.C .D
.D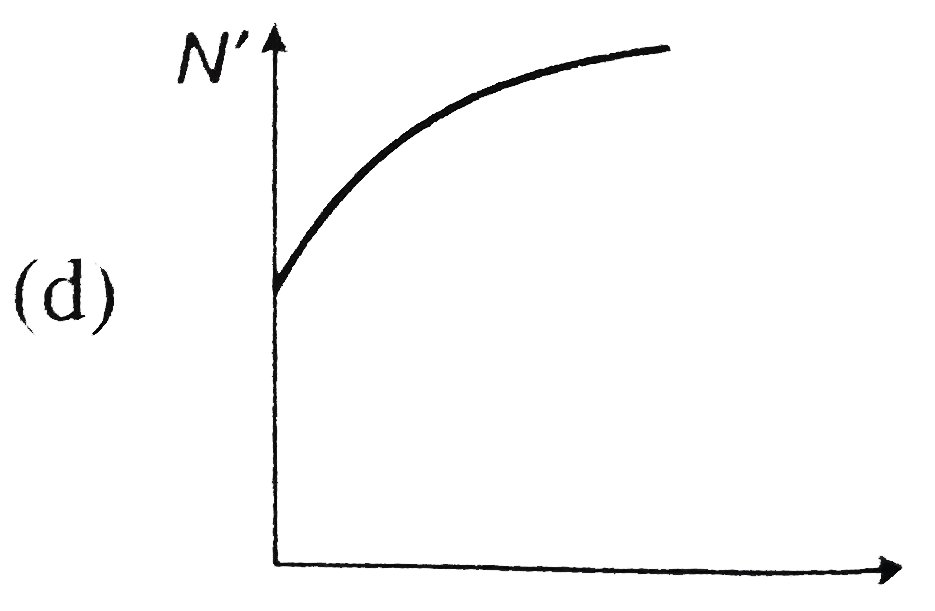 .
.Radioactive nucleus A decays into B with half-life 10sec. A also convert into C with half-life 100sec. Find half-life of A for both emission.
A6secB9secC3secD2secThe decay constant of a radioactive sample is λ. Its half -life is T1/2 and mean life is T.
AT1/2=1λ,T=In2λBT1/2=In2λ,T=1λCT1/2=λin2,T=1λDT1/2=λIn2,T=In2λ
The half life of a radioactive substance is T0. At t=0,the number of active nuclei are N0. Select the correct alternative.
View SolutionNucleus A decays into B with a decay constant λ1 and B further decays into C with a decay constant λ2 . Initially, at t = 0, the number of nuclei of A and B were 3N0 and N0 respectively. If at t = t0 number of nuclei of B becomes constant and equal to 2N0, then
View SolutionA fraction f1 of a radioactive sample decays in one mean life, and a fraction f2 decays in one half life. Then
View SolutionThe activity of a nucleus is inversely proportional to its half of average life. Thus, shorter the half life of an element, greater is its radioactivity, i.e., greater the number of atomsd disintegrating per second. The relation between half life and average life is t1/2=0.693λ=τ×0.693
or τ=1.44t1/2
The half life of a radioactive element is 10 years. What percentage of it will decay in 100 years?
View SolutionWhat is the value of decay constant of a compound having half life time of 2.95 days?
View Solution