A seconds pendulum is suspended from rof of a vehicle that is moving along a circular track of radius 10√3m with speed 10m/s. Its period of oscillation will be (g=10m/s2)
√2s
2s
1s
0.5s
The correct Answer is:A
To solve the problem of finding the period of oscillation of a seconds pendulum suspended from the roof of a vehicle moving along a circular track, we can follow these steps:
Step 1: Understand the Problem
We have a seconds pendulum (which has a period of 2 seconds) suspended from a vehicle that is moving in a circular path. The radius of the circular track is given as r=10√3 m, and the speed of the vehicle is v=10 m/s. We need to find the period of oscillation of the pendulum when the effective acceleration due to gravity is considered.
Step 2: Identify the Effective Gravity
When the vehicle is moving in a circular path, the pendulum experiences both gravitational force and centripetal acceleration. The effective acceleration g′ acting on the pendulum can be expressed as:
g′=g+ac
where ac is the centripetal acceleration given by:
ac=v2r
Substituting the values:
- g=10m/s2
- v=10m/s
- r=10√3
Step 3: Calculate Centripetal Acceleration
Now, we calculate ac:
ac=v2r=10210√3=10010√3=10√3m/s2
Step 4: Calculate Effective Gravity
Now, substituting ac back into the equation for effective gravity:
g′=g+ac=10+10√3
Step 5: Determine the Length of the Pendulum
For a seconds pendulum, the length L can be expressed as:
L=gπ2
Step 6: Calculate the Period of the Pendulum
The period T of the pendulum is given by:
T=2π√Lg′
Substituting L and g′:
T=2π
⎷gπ2g+10√3
This simplifies to:
T=2π√gπ2(g+10√3)
Step 7: Substitute the Values
Substituting g=10:
T=2π√10π2(10+10√3)=2π√1010π2(1+√3)=2√1π2(1+√3)
Step 8: Final Calculation
Now, we can calculate the numerical value of T:
T=2π√11+√3
This gives us the final period of oscillation of the pendulum.
Final Answer
The period of oscillation of the seconds pendulum is approximately √2 seconds.
---
We have a seconds pendulum (which has a period of 2 seconds) suspended from a vehicle that is moving in a circular path. The radius of the circular track is given as r=10√3 m, and the speed of the vehicle is v=10 m/s. We need to find the period of oscillation of the pendulum when the effective acceleration due to gravity is considered.
When the vehicle is moving in a circular path, the pendulum experiences both gravitational force and centripetal acceleration. The effective acceleration g′ acting on the pendulum can be expressed as:
g′=g+ac
where ac is the centripetal acceleration given by:
ac=v2r
Substituting the values:
- g=10m/s2
- v=10m/s
- r=10√3
Now, we calculate ac:
ac=v2r=10210√3=10010√3=10√3m/s2
Now, substituting ac back into the equation for effective gravity:
g′=g+ac=10+10√3
For a seconds pendulum, the length L can be expressed as:
L=gπ2
The period T of the pendulum is given by:
T=2π√Lg′
Substituting L and g′:
T=2π
⎷gπ2g+10√3
This simplifies to:
T=2π√gπ2(g+10√3)
Substituting g=10:
T=2π√10π2(10+10√3)=2π√1010π2(1+√3)=2√1π2(1+√3)
Now, we can calculate the numerical value of T:
T=2π√11+√3
This gives us the final period of oscillation of the pendulum.
The period of oscillation of the seconds pendulum is approximately √2 seconds.
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - DAMPED AND FORCED OSCILLATIONS
2 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL-II (H.W)
1 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - OSCILLATIONS DUE TO A SPRING
13 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
An electron is revolving in a circular path of radius 2×10−10 m with a speed of 3×106 m/s. The magnetic field at the centre of circular path will be-
View SolutionA simple pendulum of length l and having a bob of mass M is suspended ina car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium, what will be its time period ?
View Solution
Knowledge Check
A scooter is going round a circular road of radius 100 m at a speed of 10m/s . The angular speed of the scooter will be
A0.01rad/sB0.1rad/sC1rad/sD10rad/sA seconds pendulum is suspended form the roof of a lift. If the lift is moving up with an acceleration 9.8m/s2, its time period is
A1sB√2C1√2sD2√2sA seconds pendulum is suspended from the ceiling of a trolley moving horizontally with an acceleration of 4m/s2 . Its period of oscillation is
A1.90sB1.70sC2.30sD1.40s
A car of mass m wants to move on a circular turn of radius 120m with 30m/s .What should be the banking angle for circular turn ?(g=10m/s^(2))
View SolutionCalculate the angular speed of againt wheel of radius 10 m, moving with a speed of 10m/s.
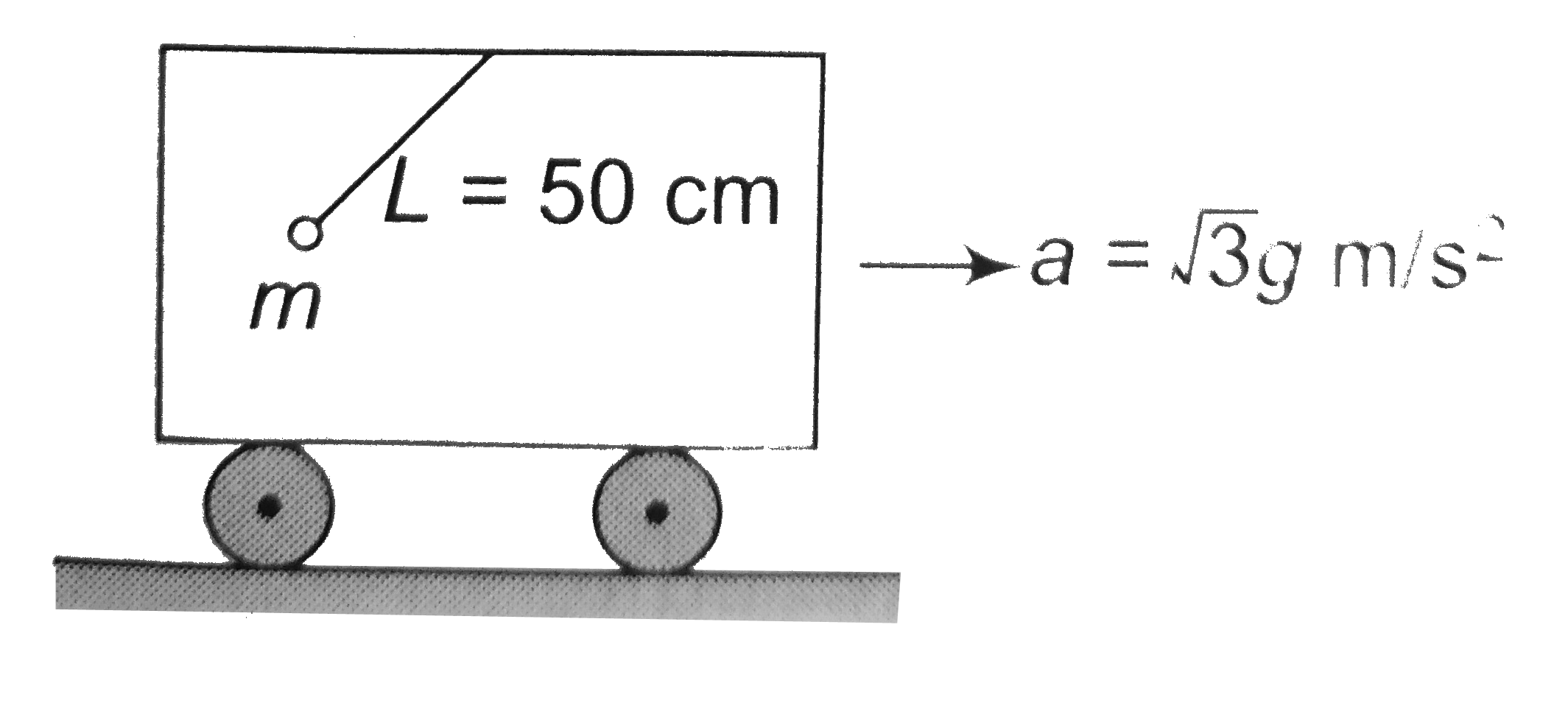
View SolutionA simple pendulum 50cm long is suspended from the roof of a acceleration in the horizontal direction with constant acceleration √3gm/s−1. The period of small oscillations of the pendulum about its equilibrium position is (g=π2m/s2) ltbRgt
View SolutionThe electron in a hydrogen atom moves in circular orbit of radius 5×10−11m with a speed of 0.6π×106m/s then
View SolutionA second pendulum is attached to roof of a car that is moving with acceleration 10m/s2 on a straight road. Its frequenct of oscillation is
View Solution
