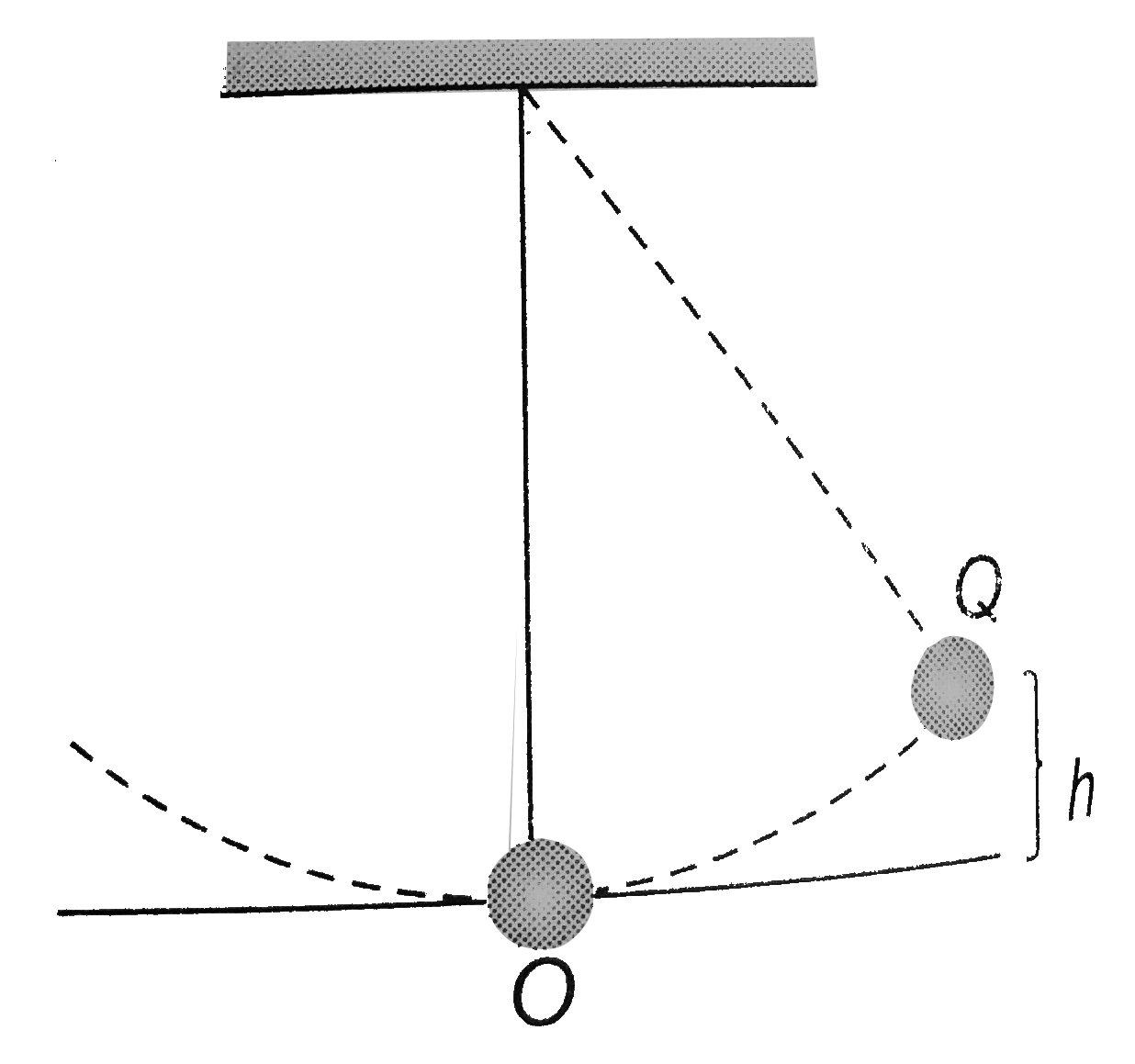
The bob of a simple pendulum is displaced from its equilibrium position 'O' to a position 'Q' which is at a height 'h' above 'O' and the bob is then released. Assuming the mass of the bob to be 'm' and time period of oscillation to be 2.0s, the tension in the string when the bob passes through 'O' is
m(g+2π2h)
m(g+π2h)
m(g+π22h)
m(g+π23h)
The correct Answer is:A
To find the tension in the string when the bob of the simple pendulum passes through the equilibrium position 'O', we can follow these steps:
Step 1: Understand the System
The bob is displaced to a height 'h' above the equilibrium position 'O' and then released. As it swings down, it will convert its potential energy at height 'h' into kinetic energy at the lowest point 'O'.
Step 2: Calculate the Velocity at Point 'O'
Using the conservation of energy, we can equate the potential energy at height 'h' to the kinetic energy at the lowest point 'O':
PE=KE
mgh=12mv2
From this, we can solve for v2:
v2=2gh
Step 3: Apply Newton's Second Law at Point 'O'
At the lowest point 'O', the forces acting on the bob are:
1. The gravitational force downward: mg
2. The tension in the string upward: T
Using Newton's second law, we can write:
T−mg=mv2L
Where L is the length of the pendulum (which is the radius of circular motion).
Step 4: Substitute the Expression for Velocity
Substituting v2 from Step 2 into the equation:
T−mg=m(2gh)L
Rearranging gives:
T=mg+2mghL
Step 5: Relate Length L to Time Period
The time period T of a simple pendulum is given by:
T=2π√Lg
Given that the time period is 2.0 seconds, we can set up the equation:
2=2π√Lg
Squaring both sides:
1=π2Lg⟹L=gπ2
Step 6: Substitute L Back into the Tension Equation
Now substitute L into the tension equation:
T=mg+2mghgπ2=mg+2mghπ2g
This simplifies to:
T=mg+2mghπ2g
Final Expression for Tension
Thus, the final expression for the tension in the string when the bob passes through 'O' is:
T=mg+2mhπ2g
The bob is displaced to a height 'h' above the equilibrium position 'O' and then released. As it swings down, it will convert its potential energy at height 'h' into kinetic energy at the lowest point 'O'.
Using the conservation of energy, we can equate the potential energy at height 'h' to the kinetic energy at the lowest point 'O':
PE=KE
mgh=12mv2
From this, we can solve for v2:
v2=2gh
At the lowest point 'O', the forces acting on the bob are:
1. The gravitational force downward: mg
2. The tension in the string upward: T
T−mg=mv2L
Where L is the length of the pendulum (which is the radius of circular motion).
Substituting v2 from Step 2 into the equation:
T−mg=m(2gh)L
Rearranging gives:
T=mg+2mghL
The time period T of a simple pendulum is given by:
T=2π√Lg
Given that the time period is 2.0 seconds, we can set up the equation:
2=2π√Lg
Squaring both sides:
1=π2Lg⟹L=gπ2
Now substitute L into the tension equation:
T=mg+2mghgπ2=mg+2mghπ2g
This simplifies to:
T=mg+2mghπ2g
Thus, the final expression for the tension in the string when the bob passes through 'O' is:
T=mg+2mhπ2g
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - NCERT BASED QUESTIONS
1 Video
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - MULTIPLE ANSWER QUESTIONS
23 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL -II (C.W)
36 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
The bob of pendulum of length l is pulled aside from its equilibrium position through an angle θ and then released. Find the speed v with which the bob passes through the equilibrium position.
View SolutionThe string of a pendulum is horizontal. The mass of the bob is m. Now the string is released. The tension in the string in the lowest position is -
View Solution
Knowledge Check
The bob of a simple pendulum it displaced position O to a equilibrium position Q which is at height it above O and the bob to then mass released Assuming the mass of the bob to be m and 2.0 sec of oscillation to be string when the bob passes through O is
 Am(g+π√2gh)Bm(g+π√π2gh)Cm(g+√π22gh)Dm(g+√π23gh
Am(g+π√2gh)Bm(g+π√π2gh)Cm(g+√π22gh)Dm(g+√π23ghA simple pendulum of length l and bob of mass m is displaced from its equilibrium position O to a position P so that height of P above O is h . If is then released. What is the tension in the string when the bob passes through the through the equilibrium position O ? Neglect friction. v is the velocity of the bob at O
Am(g+v2l)B2mghlCmg(1+hl)Dmg(1+2hl)The bob of simple pendulum having length 1, is displaced from mean position to an angular position o with respect to vertical. If it is released, then velocity of bob at equilibrium position is
A√2g(1−cosθ)B√2g(1+cosθ)C√2glcosθD√2gl
The bob of a simple pendulum of length L, is displaced through 90∘, from its mean position and then released. What will be the tension in the string when the bob of mass m will be its lowest position ?
View SolutionThe bob of a simple pendulum of length L, is displaced through 90∘, from its mean position and then released. What will be the tension in the string when the bob of mass m will be at its lowest position?
View SolutionThe periodic time of a simple pendulum is 3 sec. The mass of its hollow spherical bob is 100 gram. The bob is then filled with sand, so that the mass of the bob becomes 200 gram. Then the new period of oscillation of the simple pendulum wil be
View SolutionThe bob of a pendulum of length l is pulled a side from its equilibrium position through an angle θ and then released the bob will then pass through its equilibrium position with a speed v where v equals to
View SolutionThe bob of a pendulum of length l is pulled a side from its equilibrium position through an angle θ and then released the bob will then pass through its equilibrium position with a speed v where v equals to
View Solution