A particle of mass 4g is in a gravitational potential V=(800x2+150)erg/g. Its frequency of oscillation is
5πHz
15πHz
50πHz
50πHz
The correct Answer is:B
To find the frequency of oscillation for a particle of mass 4g in the given gravitational potential V=800x2+150 erg/g, we can follow these steps:
Step 1: Understand the potential energy
The gravitational potential V is given as:
V=800x2+150 erg/g
This represents the potential energy per unit mass.
Step 2: Calculate the potential energy U
The total potential energy U of the particle can be calculated by multiplying the potential V by the mass m:
U=V⋅m=(800x2+150)⋅4 g
U=3200x2+600 erg
Step 3: Determine the force F
The force F acting on the particle is given by the negative gradient of the potential energy:
F=−dUdx
We differentiate U with respect to x:
dUdx=ddx(3200x2+600)=6400x
Thus, the force is:
F=−6400x
Step 4: Relate force to acceleration
According to Newton's second law, F=ma, where m is the mass of the particle. Therefore:
ma=−6400x
Since the mass m=4g (or 0.004 kg), we can simplify:
4a=−6400x⟹a=−1600x
Step 5: Identify the oscillation equation
The equation a=−1600x is in the form of simple harmonic motion (SHM), which can be expressed as:
a=−ω2x
From this, we can identify:
ω2=1600⟹ω=√1600=40 rad/s
Step 6: Calculate the frequency f
The relationship between angular frequency ω and frequency f is given by:
ω=2πf
Thus, we can solve for f:
f=ω2π=402π=20π Hz
Final Answer
The frequency of oscillation is:
f=20π Hz
---
The gravitational potential V is given as:
V=800x2+150 erg/g
This represents the potential energy per unit mass.
The total potential energy U of the particle can be calculated by multiplying the potential V by the mass m:
U=V⋅m=(800x2+150)⋅4 g
U=3200x2+600 erg
The force F acting on the particle is given by the negative gradient of the potential energy:
F=−dUdx
We differentiate U with respect to x:
dUdx=ddx(3200x2+600)=6400x
Thus, the force is:
F=−6400x
According to Newton's second law, F=ma, where m is the mass of the particle. Therefore:
ma=−6400x
Since the mass m=4g (or 0.004 kg), we can simplify:
4a=−6400x⟹a=−1600x
The equation a=−1600x is in the form of simple harmonic motion (SHM), which can be expressed as:
a=−ω2x
From this, we can identify:
ω2=1600⟹ω=√1600=40 rad/s
The relationship between angular frequency ω and frequency f is given by:
ω=2πf
Thus, we can solve for f:
f=ω2π=402π=20π Hz
The frequency of oscillation is:
f=20π Hz
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - NCERT BASED QUESTIONS
1 Video
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - MULTIPLE ANSWER QUESTIONS
23 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL -II (C.W)
36 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
Knowledge Check
A particle of mass 10gm is placed in a potential field given by V=(50x2+100)J/kg. The frequency of oscilltion in cyc≤/sec is
A10πB5πC100πD50πA particle of mass 5 kg is placed in a field of gravitational potential
v=(7x2−21x)J/kg . Then its motionAis SHM with angular frequency 1.67rad/sBis SHM with angular frequency 3.74rad/sCIs oscillarotry but no SHMDis SHM with amplitude 5.5mWhen a particle oscillates simple harmonically, its potential energy varies periodically. If the frequency of oscillation of the particle is n, the frequency of potential energy variation is
An/2BnC2nD4n
If gravitational potential is V=xy2, find the gravitational field at (2,1)
View SolutionA particle of mass = 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is nπ5 second. Find value of n.
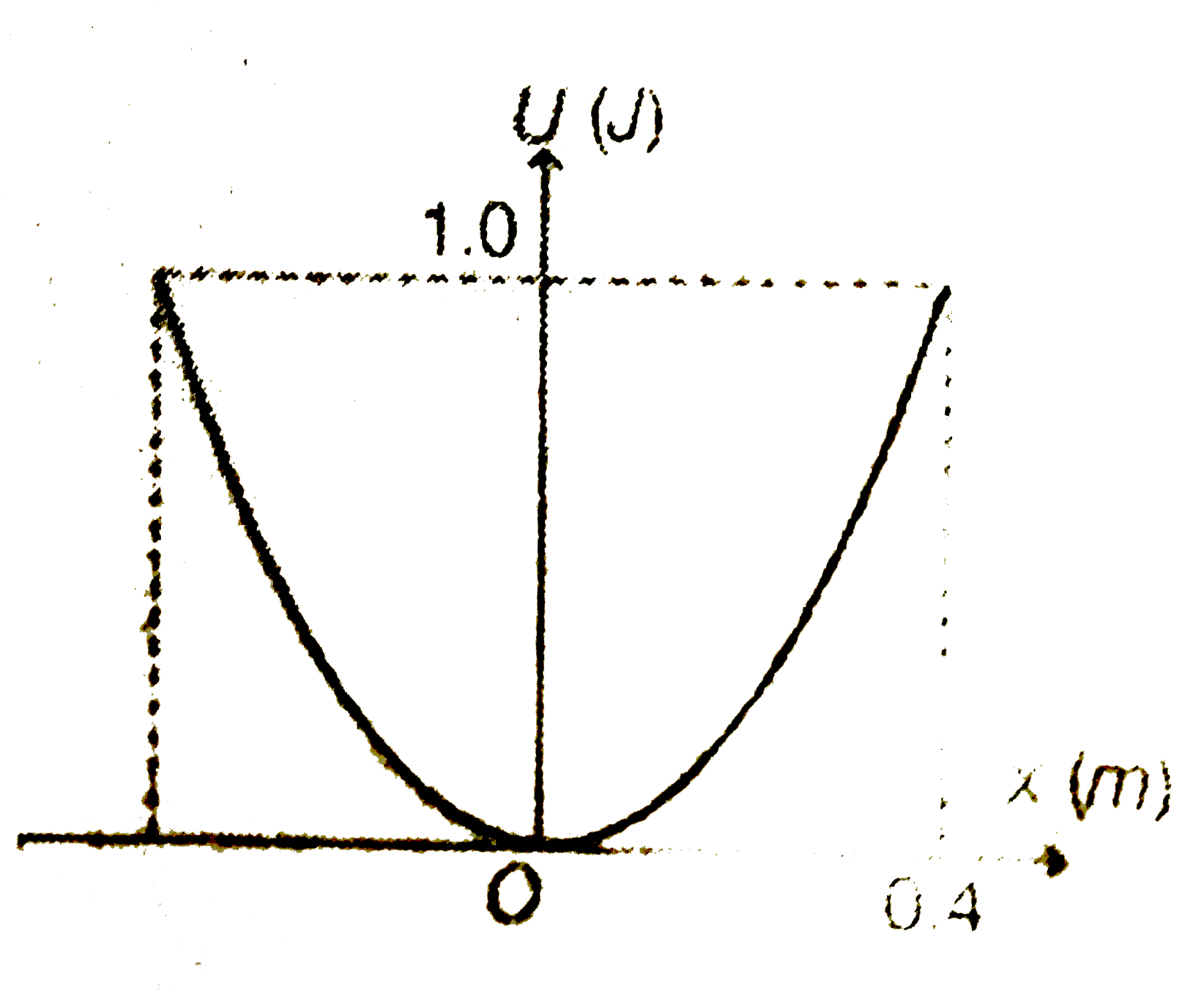
View SolutionA particle of mass m moves in a one dimensional potential energy U(x)=−ax2+bx4, where a and b are positive constant. The angular frequency of small oscillation about the minima of the potential energy is equal to
View SolutionA partical of mass m is moving along the x-axis under the potential V(x)=kx22+λ Where k and x are positive constants of appropriate dimensions . The particle is slightly displaced from its equilibrium position . The particle oscillates with the the angular frequency (ω) given by
View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View Solution
