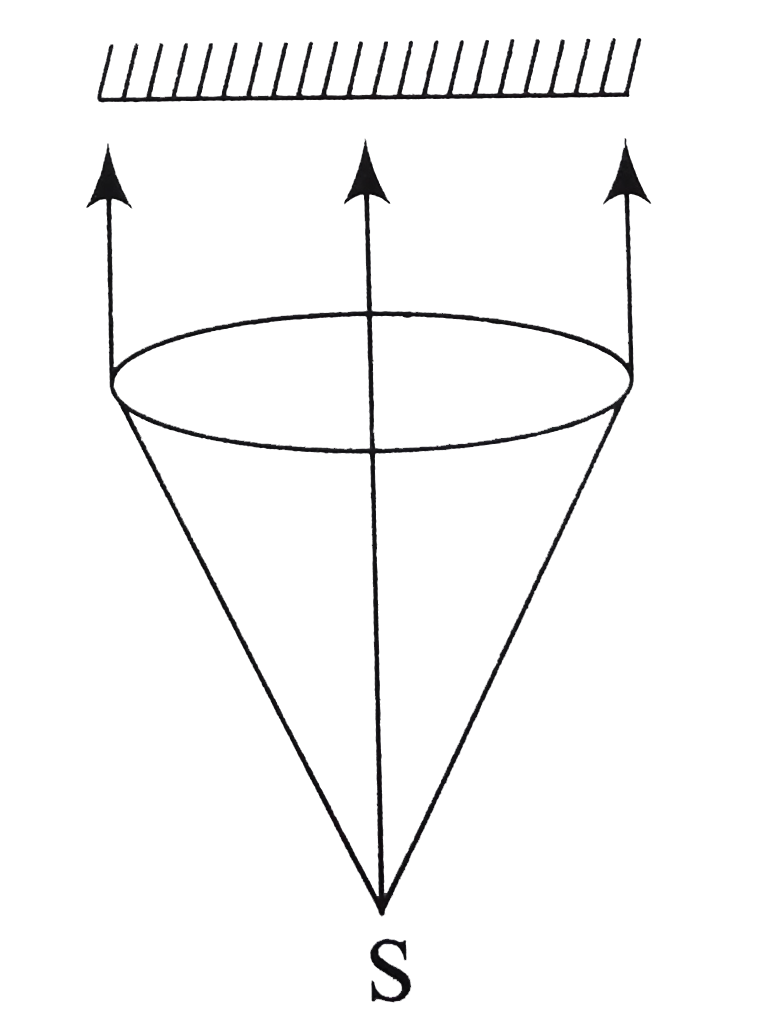
A totally reflecting, small plane mirror placed horizontally faces a parallel beam of light as shown in the Fig. The mass of the mirror is 20 g. Assume that there is no absorption in in the lens and that 30% of the light emitted by the source goes through the lens. Find the power (in×108W) of the source needed to support the weight of the mirror. Take g=10ms−2
(a) Let P: power of lens. 30% of light passes through lens and light is completely reflected.
Force exerted by lilght =2(0.3P)c=0.6Pc
Weight of mirror = mg
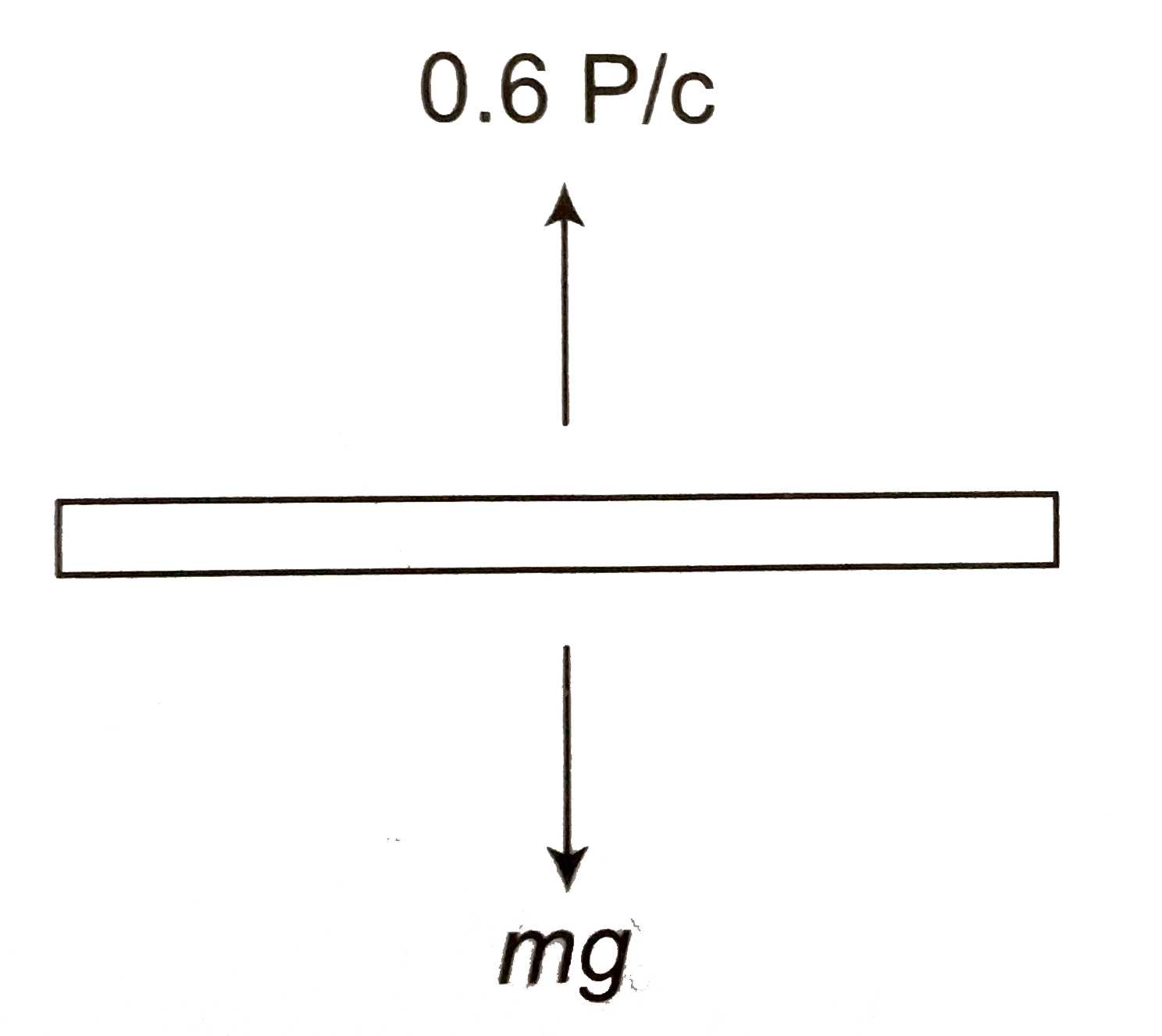
In equilibrium
0.6Pc=mg
P=mgc0.6=20×10−3×10×3×1080.6=108W
(b) 
Intensity of light at surface
I=0.6P4πr2
Pressure exerted by light
p=Ic=0.6P4πr2c=110×0.64π(0.2)2×3×108
=4.4×10−6N/m2
(c) 
(i) Force exerted by light F=P/c
tanθ=P/cmg=Pmgs
θ=tan−1(Pmgc)
(ii) Time period of simple pendulum
T=2π√La
a: effective acceleration.
a=√(mg)2+(P/c)2m
√g2+(Pmc)2
T=2π√L[g2+(Pmc)2]1/4
Topper's Solved these Questions
Similar Questions
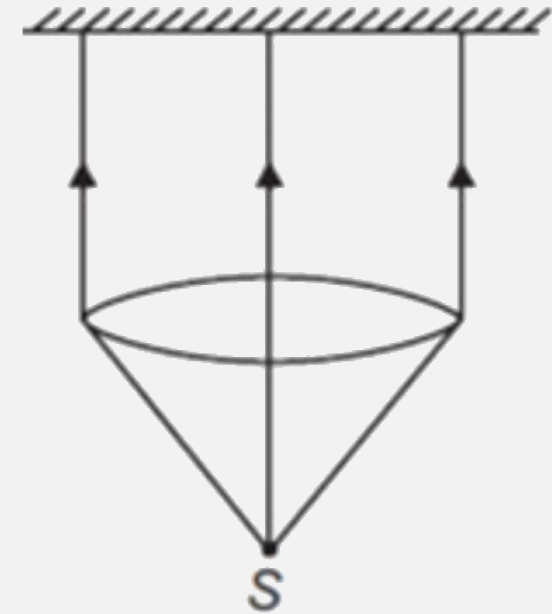
A totally reflecting, small plane mirror placed horizontally faces a parallel beam of lighy as shown in figure. The mass of the mirror is 20g. Assume that there is no absorption in the lens and that 30% of the light emitted by the source goes through the lens. Find the power of the source needed to support the weight of the mirror. Take g= 10 m s^-2.
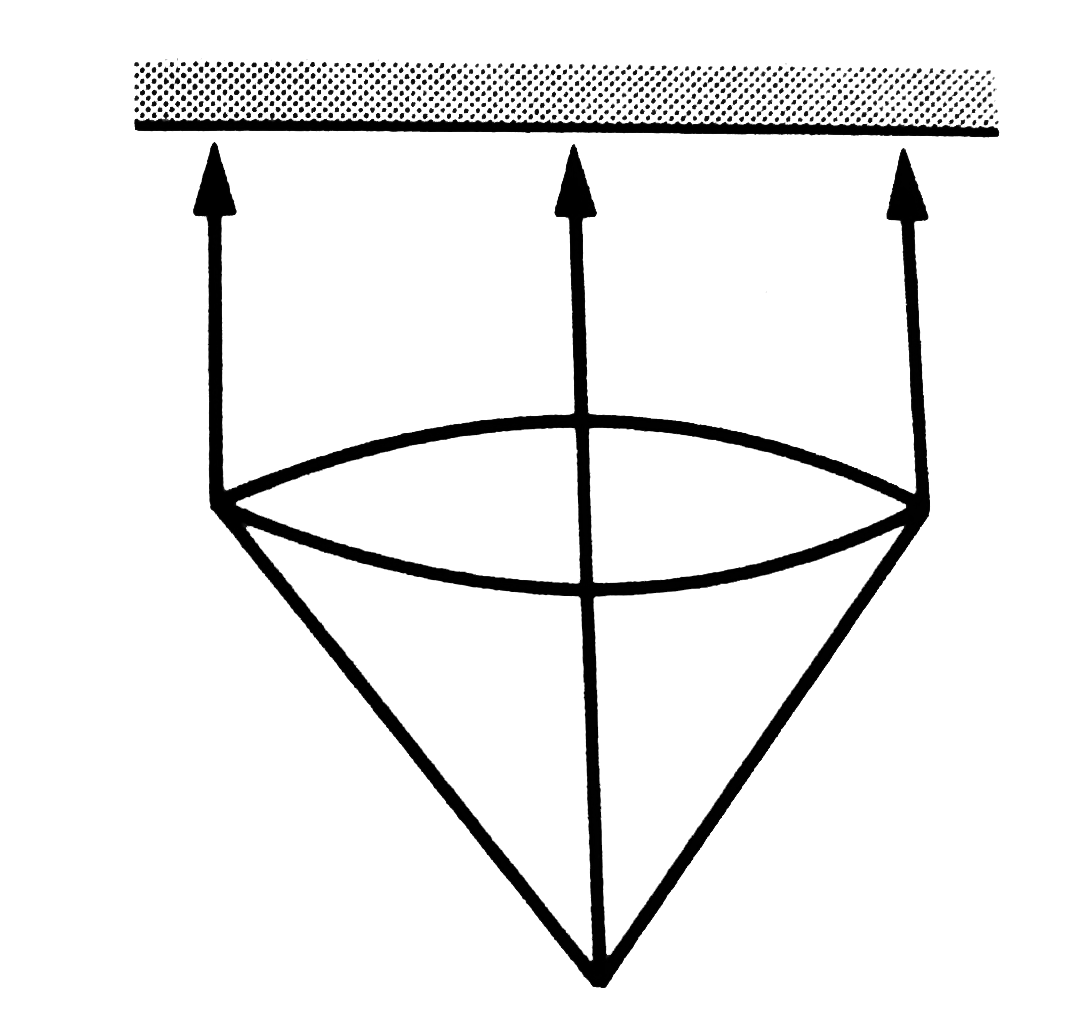
View SolutionA totally reflecting small plane mirror placed horizontally faces a parallel beam of light as shown in the figure. The mass of the mirror is 200 g. Assume that there is no absorption in the lens and that 20% of the light emitted by the source goes through the lens. The power of the source needs to support the weight of the mirror is P×108 watt, where P is [take g=10ms−2]
View Solution
Knowledge Check
A convex lens of focal length 15 cm and concave mirror of focal length 30 cm are kept their optical axes PQ and RS parallel but separated in vertical direction by 0.6 m, as shown. The distance between the lens and mirror is 30 cm. An upright object AB of height 1.2 m is placed on the optic axic PQ of the lens at a distance of 20 cm from the lens.

Find the linear magnification of the second image after reflection from the mirror.A+2B−2C+12D−12The separation between the screen and a plane mirror is 2 r . An isotropic point source of light is placed exactly midway between the mirror and the screen. Assume that mirror reflects 100% of incident light. Then the ratio of illuminances on the screen with and without the mirror is
A10:1B2:1C10:9D9:1A point source of light is placed at 2f from a converging lens of focal length f. A flat mirror is placed on the other side of the lens at a distanc d such that rays reflected from the mirror are parallel after passing through the lens again. If f = 30 cm, then d is equal to
A15 cmB30 cmC45 cmD75 cm
A converging lens and a diverging mirror are placed at a separation of 20 cm. The focal length of the lens is 30 cm and that of the mirror is 50 cm. Where should a point source be placed between the lens and the miror, so that the light, after getting reflected by the mirror and then getting transmitted by the lens, comes out parallel to the principal axis?
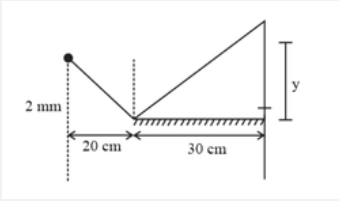
View SolutionA plane mirror of length 30 cm is placed horizontally along with a vertical screen. A monochromatic point source of light is placed 20 cm to the left off the left edge of the mirror, at a height of 2 mm above the plane of the mirror. If the wavelength of light used is 6400Å, then find the number of complete bright fringes formed.
View SolutionTwo identical mirrors are placed in a hollow cylindrical tube as show in the figure. A light ray incident on one of the mirrors undergoes multiple reflections. In the length of each mirror is 3 m, and the velocity of light is 3×108ms−1, then find the time raken by the light ray incident on the mirror to come out of the bollow cylinder.
View SolutionTwo identical mirrors are placed in a hollow cylindrical tube as show in the figure. A light ray incident on one of the mirrors undergoes multiple reflections. In the length of each mirror is 3 m, and the velocity of light is 3×108ms−1, then find the time raken by the light ray incident on the mirror to come out of the bollow cylinder.
View SolutionA source of light is located at double focal length from a convergent lens. The focal length of the lens is f=30cm. At what distance from the lens should a flat mirror be placed, so that the rays reflected from the mirror are parallel after passing through the lens for the second time?
View Solution