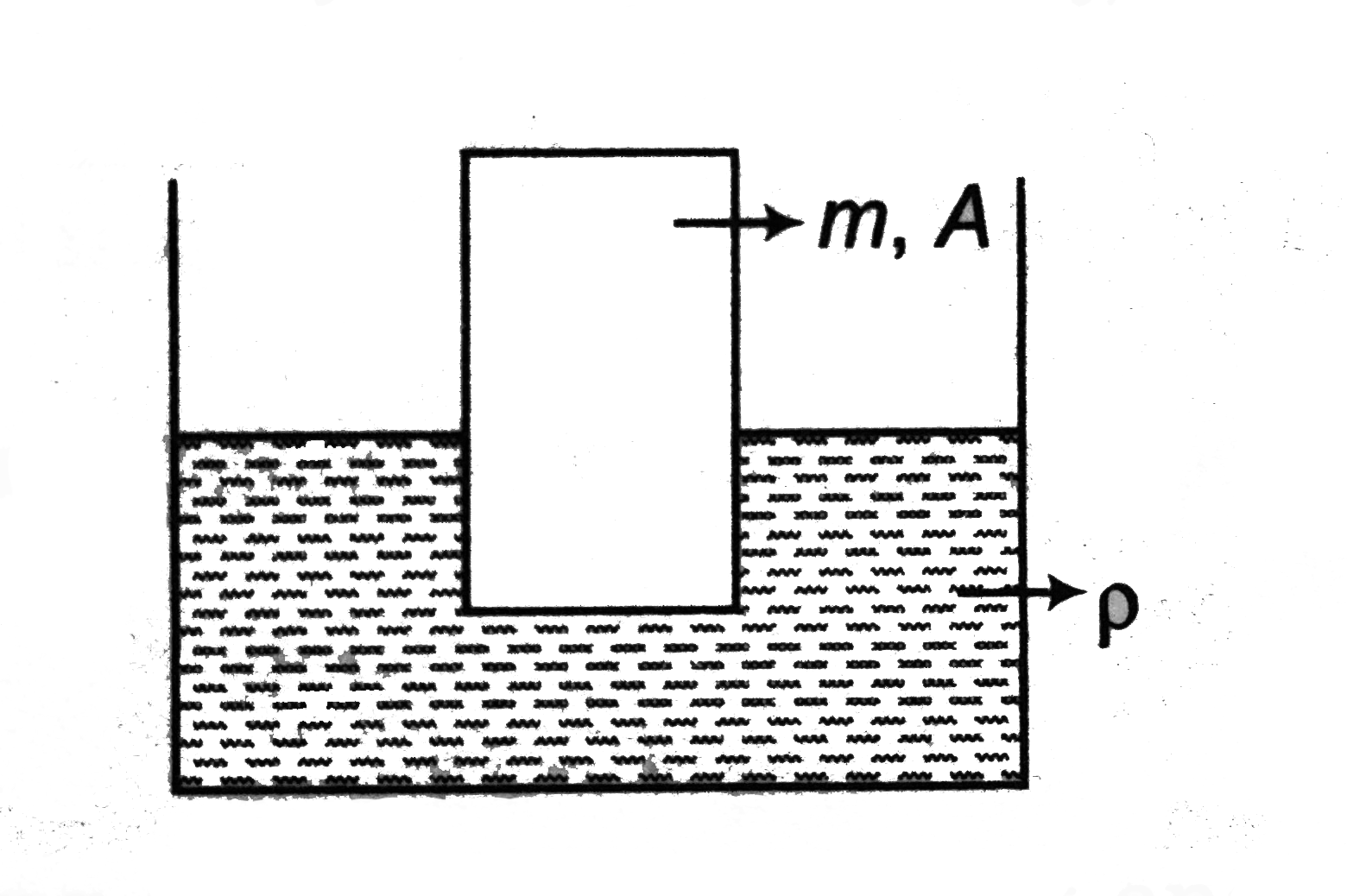
A rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T.
(i) T∝√m
(ii) T∝√ρ
(iii) T∝1√A
(iv) T∝1√ρ.
(i),(ii),(iii)
(i),(iii),(iv)
(i),(iii)
(iii),(iv)
The correct Answer is:B
To solve the problem, we need to analyze the oscillation of a rectangular block floating in a liquid. Let's break down the steps:
Step 1: Understand the forces acting on the block
When the block is floating in equilibrium, the weight of the block (W) is balanced by the buoyant force (FB). The weight of the block is given by:
W=mg
where m is the mass of the block and g is the acceleration due to gravity.
The buoyant force is given by Archimedes' principle:
FB=ρVg
where ρ is the density of the liquid, and V is the volume of the liquid displaced by the block. For a rectangular block with area of cross-section A and height H, the volume displaced is:
V=A⋅h
where h is the height of the submerged part of the block.
Step 2: Establish equilibrium condition
At equilibrium, the weight of the block equals the buoyant force:
mg=ρAHg
This gives us the relationship between the mass of the block, the area of cross-section, and the density of the liquid.
Step 3: Analyze small vertical displacements
When the block is displaced vertically by a small distance y, the new submerged volume becomes:
V′=A(H+y)
The new buoyant force is:
F′B=ρA(H+y)g
The change in buoyant force due to the displacement is:
ΔFB=F′B−FB=ρA(H+y)g−ρAHg=ρAyg
Step 4: Determine the restoring force
The restoring force acting on the block when it is displaced by y is given by:
F=−ΔFB=−ρAyg
Step 5: Apply Newton's second law
According to Newton's second law, the acceleration a of the block can be expressed as:
ma=−ρAyg
This can be rewritten as:
a=−ρAgmy
Step 6: Relate to simple harmonic motion
This equation is of the form:
a=−ω2y
where ω2=ρAgm.
Step 7: Find the time period T
The time period T of oscillation is related to the angular frequency ω by:
T=2π√mρAg
Step 8: Analyze the proportional relationships
From the expression for T:
1. T∝√m (True)
2. T∝√ρ (False)
3. T∝1√A (True)
4. T∝1√ρ (False)
Conclusion
The correct proportional relationships are:
- T∝√m
- T∝1√A
Thus, the correct options are (i) and (iii).
When the block is floating in equilibrium, the weight of the block (W) is balanced by the buoyant force (FB). The weight of the block is given by:
W=mg
where m is the mass of the block and g is the acceleration due to gravity.
FB=ρVg
where ρ is the density of the liquid, and V is the volume of the liquid displaced by the block. For a rectangular block with area of cross-section A and height H, the volume displaced is:
V=A⋅h
where h is the height of the submerged part of the block.
At equilibrium, the weight of the block equals the buoyant force:
mg=ρAHg
This gives us the relationship between the mass of the block, the area of cross-section, and the density of the liquid.
When the block is displaced vertically by a small distance y, the new submerged volume becomes:
V′=A(H+y)
The new buoyant force is:
F′B=ρA(H+y)g
The change in buoyant force due to the displacement is:
ΔFB=F′B−FB=ρA(H+y)g−ρAHg=ρAyg
The restoring force acting on the block when it is displaced by y is given by:
F=−ΔFB=−ρAyg
According to Newton's second law, the acceleration a of the block can be expressed as:
ma=−ρAyg
This can be rewritten as:
a=−ρAgmy
This equation is of the form:
a=−ω2y
where ω2=ρAgm.
The time period T of oscillation is related to the angular frequency ω by:
T=2π√mρAg
From the expression for T:
1. T∝√m (True)
2. T∝√ρ (False)
3. T∝1√A (True)
4. T∝1√ρ (False)
The correct proportional relationships are:
- T∝√m
- T∝1√A
Topper's Solved these Questions
Similar Questions
A plank of mass 'm' and area of cross - section A is floating in a non - viscous liquid of desity ρ. When displaced slightly from the mean position, it starts oscillating. Prove that oscillations are simple harmonic and find its time period.
View SolutionA rectangular block of mass m and area of cross section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium it undergoes with a time period T, then
View Solution
Knowledge Check
A rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
AT∝√ρBT∝1√ACT∝1ρDT∝1√mA rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
AT∝√ρBT∝1√ACT∝1√ρDT∝1√mA rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
AT∝√ρBT∝1√ACT∝1∝DT∝1√m
A rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is givan a small vertical displacement from equilibrium, it undergoes oscillation with a time period T, then select the wrong alternative.
View SolutionA block of rectangular size of mass m and area of cross section A, float in a liquid of density ρ.If we give a small vertical displacement from equilibrium, It undergoes SHM with time period T, then
View SolutionA rectangular block of mass m and area of cross a small vertical displacement from equilibrium it undergoes oscillation with a time period T then
View SolutionA cylinderical block of wood of mass m and area cross-section A is floating in water (density = ρ) when its axis vertical. When dressed a little and the released the block starts oscillating. The period oscillations is
View SolutionAccording to the kinetic theory of gases
(i) P∝vrms
(ii) vrms∝T
(iii) vrms∝T1/2
(iv) P∝v2rms
View Solution

