A liquid of density 800kg/m3 flowing steadily in a tube of varying cross-section. If area of cross-section at A is 4cm2 and at B is 2cm2. If speed of liquid at A is 10cm/s, calculate
(i) the rate of flow
(ii) the difference in pressures at A and B.
(i) Rate of flow Q=aAvA=aBvB
Q=aAvA=4×10−4×10×10−2=4×10−5m3/s
(ii) From continuity equation
aAvA=aBvB
4×10=2×vB⇒v2=20cm/s
Applying Bernoulli's equation
PA+ρghA+12ρv2A=PB+ρghB+12ρv2B
Here hA=hB
PA−PB=12ρ(v2B−v2A)=12×800(202−102)×10−4
=400×300×10−4
=12N/m2.
Topper's Solved these Questions
Similar Questions
Figure shows a liquid of densith 1200kgm−3 flowing steadily in a tube of varying cross section. The cross section at a point A is 1.0cm2 and that at B is 20mm2, the points A and B are in the same horizontal plane.The speed of the liquid at A is 10 cms−1. Calculate the difference in pressure at A and B.

View SolutionWater flows through a tube shown in figure. The areas of cross section at A and B are 1cm2and0.5cm2 respectively. The height difference between A and B is 5m. If the speed of water at A is 10 cms−1 find a the speed at B and b the difference in pressures at A and B.

View Solution
Knowledge Check
A non viscous liquid of constant density 103kg/m3 flows in stream line motion along a vertical tube PQ of variable cross-section. Height of P and Q are 2m and 2.5m respectively. Area of tube at Q is equal to 3 times the area of tube at 'P'. Then work done per unit volume by pressure as liquid flows from P and Q. Speed of liquid at 'P' is 3m/s.
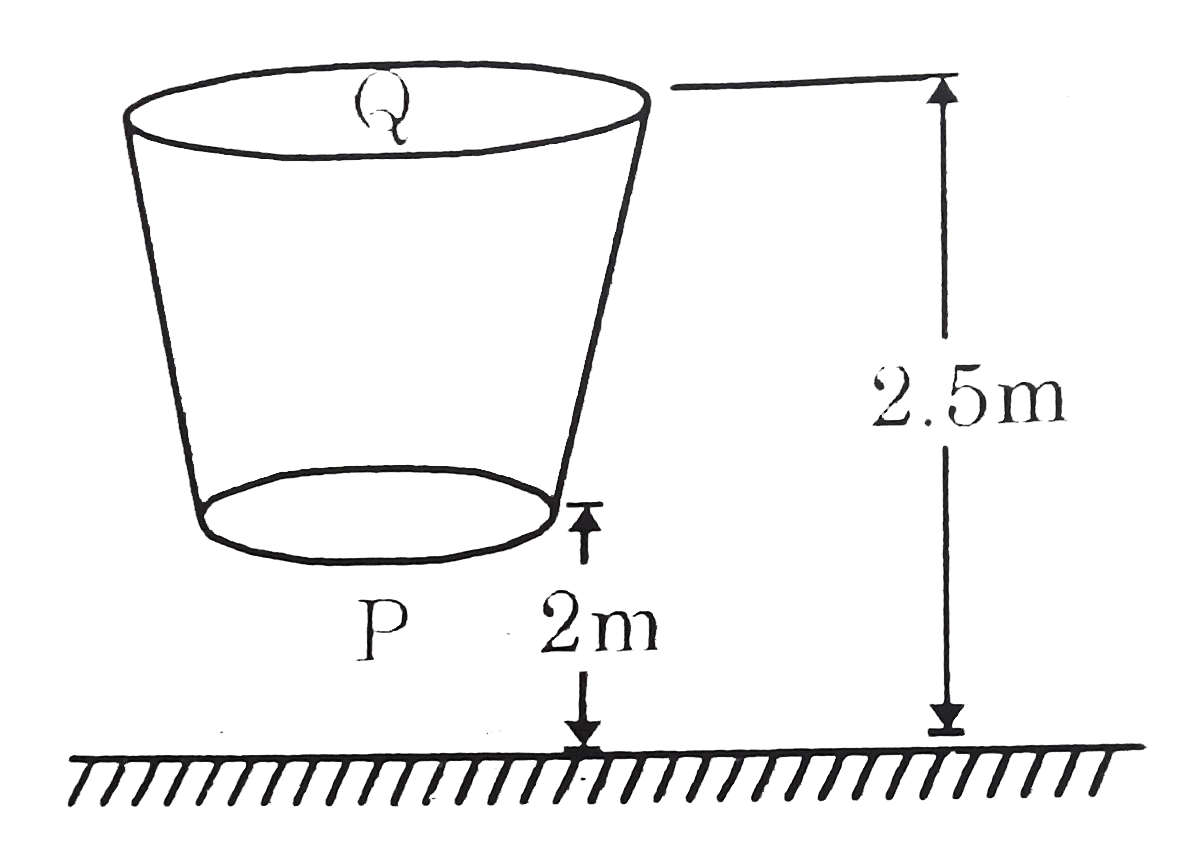 A2000J/m3B1000J/m3C1500J/m3D9000J/m3
A2000J/m3B1000J/m3C1500J/m3D9000J/m3In the previous question, at the mouth of the tap the area of cross-section is 2.5cm2 and the speed of water in 3m/s. The area of cross-section of the water column 80cm below the tap is.
A2cm2B1.5cm2C1cm2D0.5cm2
A liquid uis flowing through a pape of varying cross-section. At a certain cross-section,the dimerter of the pipe is 5 cm and Velocity of flow of the liquid is 25cms−1. Colculate the velocity of flow at another cross-sectionwhere the dimeter is 1 cm.
View SolutionA liquid is flowing through a horizontal pipe line of varying cross - section .At a certin point the diameter of the pipe is 6cm and the velocityof flow of liquid is2.0cms−1 Calculate the velocity of flow at another point where the diameter is 1.5 cm.
View SolutionA non-viscous liquid of constant density 500kg/m3 flows in a variable cross-sectional tube. The area of cross section of the tube at two points P and Q at heights of 3m and 6m are 2×10−3m3 and 4×10−3m3, respectively. Find the work done per unit volume by the forces of gravity as the fluid flows from point P to Q.
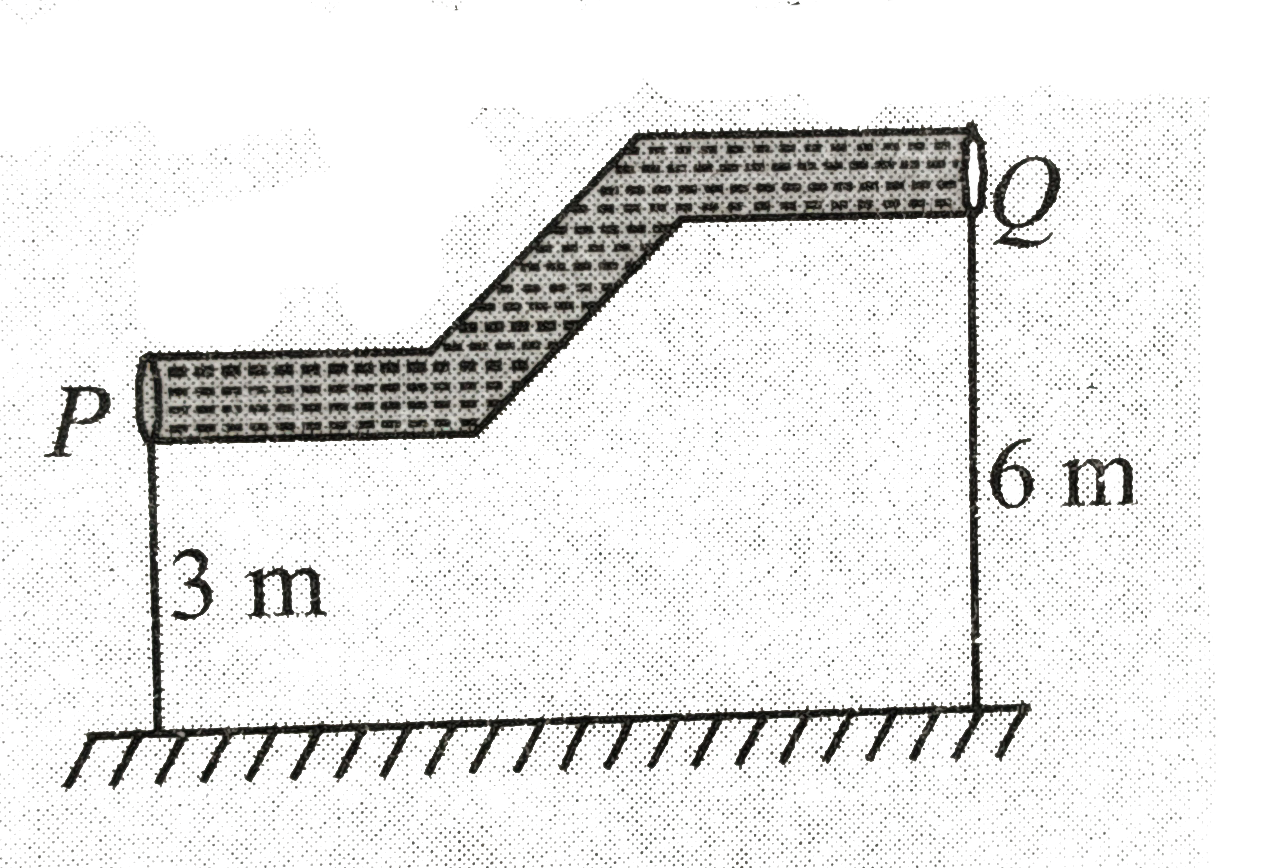
View SolutionIn this figure, an ideal liquid flows through the tube having uniform area of cross-section and is held in vertical plane. Find the ratio of speed of liquid at A and B and also find the pressure difference between- these points.

View SolutionWaster flows throgh a horizontal tube of variable cross section.The area of cross section at A and B are 4 mm2and2mm2 respectively. If 1 cc of water enters per seconds through. A find a. The speed of water at A, b. the speed of river at B and c. the pressure difference PA−PB.

View SolutionFigure shows a liquid being pushed out of a tube by pressing a piston. The area of cross section of the piston is 1.0 cm^2 and that of the tube at the outlet is 20mm2. If the piston is pushed at a speed of 2cms−1. What is the speed of the outgoing liquid?

View Solution
