A cube ofice of edge 4 cm is placed in an empty cylindrical glass of inner diameter 6 cm. Assume that the ice melts uniformly from each side so that it always retains its cubical shape. Remembering that ice lighter than water, finding the length of the edge of the ice cube at the instant it just leaves contact with the bottom of the glass.
Let edge of cube is a when some ice is melted.
Mass of melted ice = mass of water formed
σice(43−a3)=ρω[π(3)2−a2]h
0.9(64−a3)=1(9π−a2)h..(i)
FB+N=mg,N=0, when cube leaves contact
ρωa2h=σicea2g
h=0.9a ....(ii)
Form (i) and (ii)
0.9(64−a3)=(9π−a2)(0.9a)
64−a3=9πa−a3
a=649πcm
=2.26cm.

Topper's Solved these Questions
Similar Questions
A cube of ice of edge 4 cm is placed in an empty cylindrical glass of inner diameter 6 cm. Assume that the ice melts uniformly from each side so that it always retains its cubical shape. Remembering that ice is lighter than water, find the length (in cm) of the edge of the ice at the instant it just leaves the contact with the bottom of the glass.
View SolutionAn ice cube of edge a is placed in an empty cylindrical vessel of radius 2a. Find the edge (in cm) of ice cube when it just leaves the contact with the bottom assuming that ice melts uniformly maintaining its cubical shape. Take a = 12 π cm (Ice is lighter than water)
View Solution
Knowledge Check
3 ice cubes of side π cm when dropped into a cylindrical glass of base diameter 2π cm increase the level of water in the glass by 3 cm.
A(i)(ii)(iii)(iv)FTTFB(i)(ii)(iii)(iv)TTFFC(i)(ii)(iii)(iv)TFTTD(i)(ii)(iii)(iv)TFTFTwo ice cubes of side 10cm, having cavity of volume 20cm3 at centre of cube but filled with different materials A and B respectively. The specific gravity of material B is 1.9 Now these cubes are placed in two different vessels of same base area as shown in figure. The water level before putting blocks in vessels are same Assume that ice melts uniformly from all sides and with same constant rate in both the vessels. (specific gravity of ice=0.9)
 Choose the correct graph showing the variation of heights of water- level in two vessels with timeA
Choose the correct graph showing the variation of heights of water- level in two vessels with timeA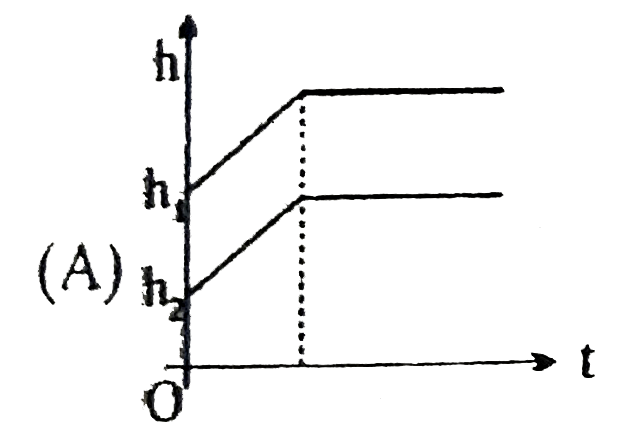 B
B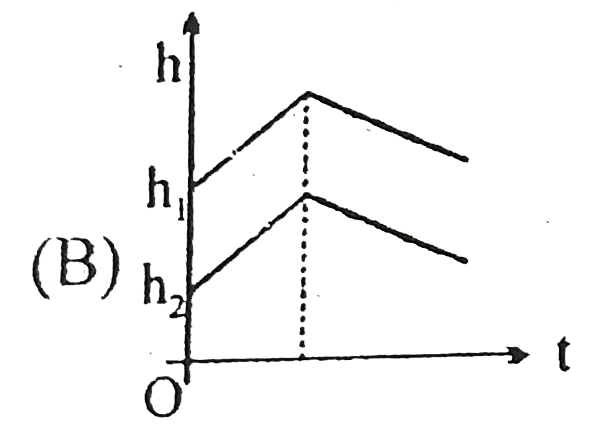 C
C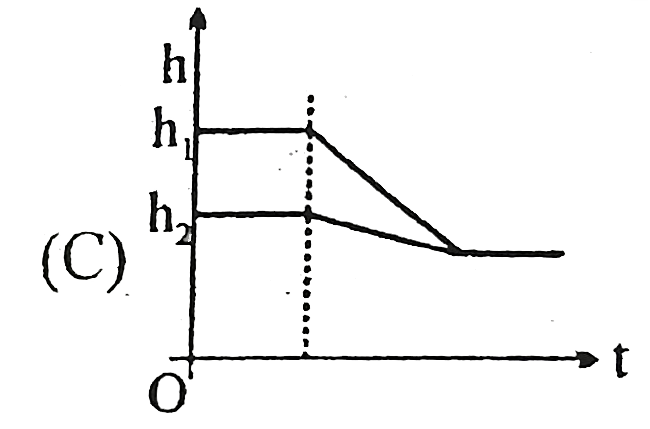 D
D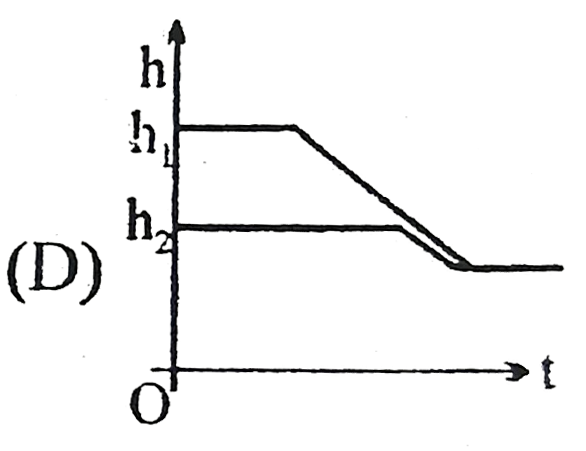
Two ice cubes of side 10cm, having cavity of volume 20cm3 at centre of cube but filled with different materials A and B respectively. The specific gravity of material B is 1.9 Now these cubes are placed in two different vessels of same base area as shown in figure. The water level before putting blocks in vessels are same Assume that ice melts uniformly from all sides and with same constant rate in both the vessels. (specific gravity of ice=0.9)
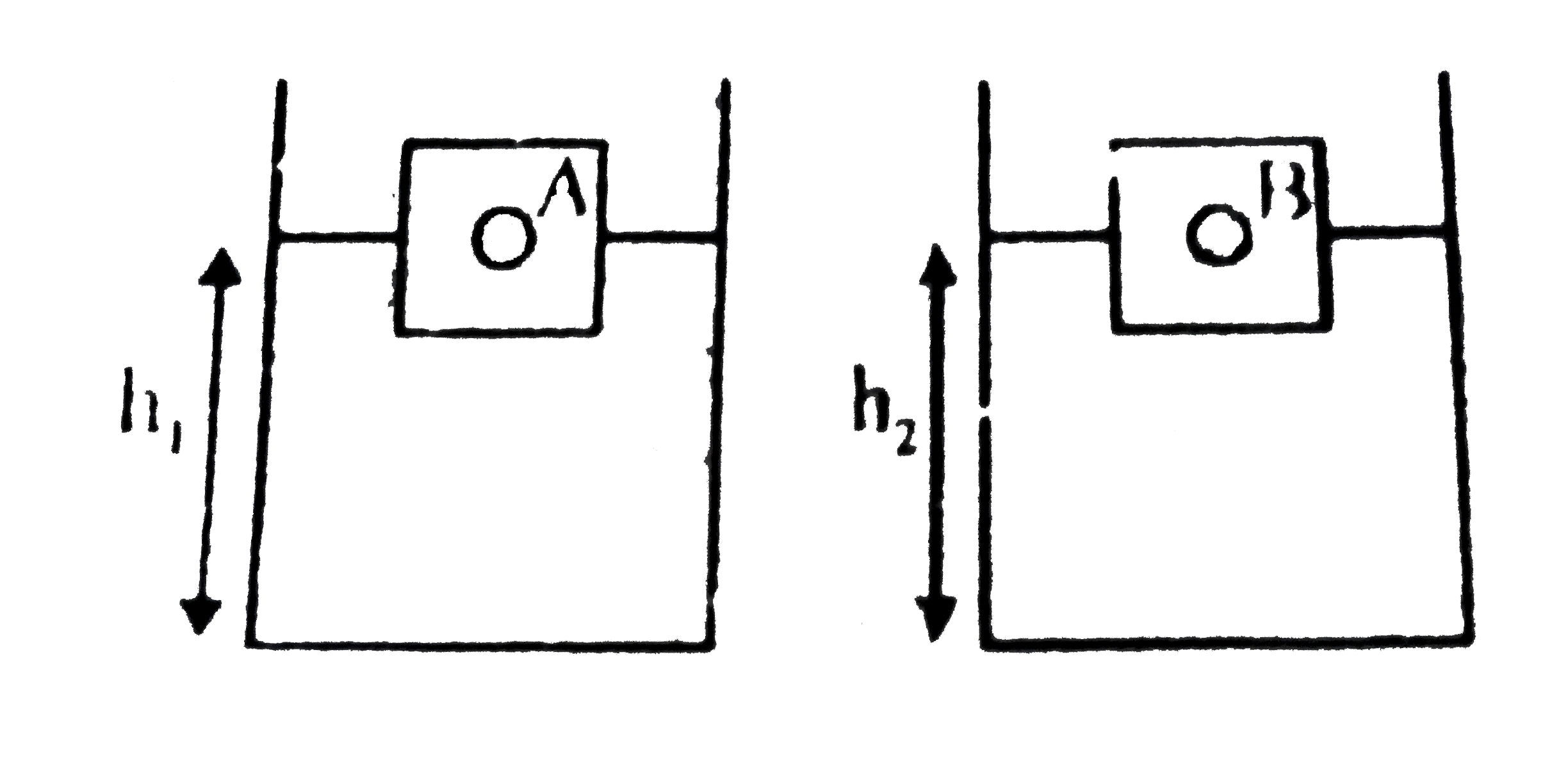 Find the ratio of initial submerged volumes of the blocks containing A and B respectivelyA4946B1:1C4919D4:1
Find the ratio of initial submerged volumes of the blocks containing A and B respectivelyA4946B1:1C4919D4:1
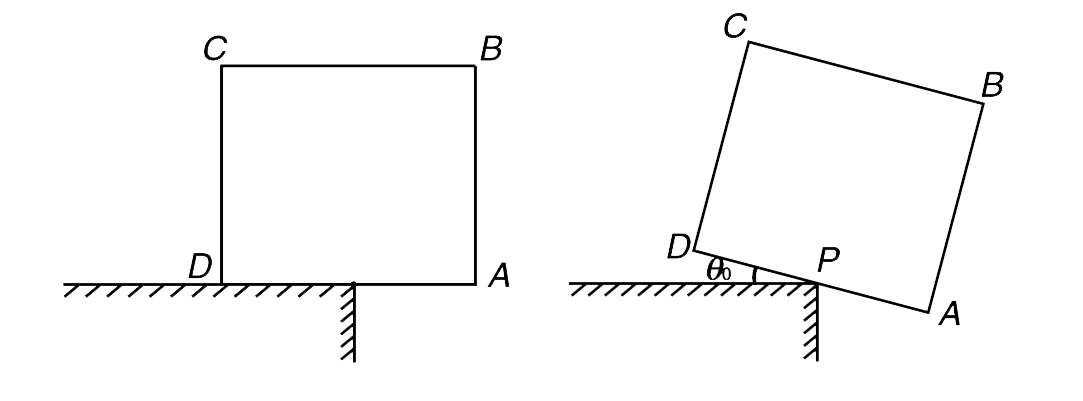
A uniform cube of mass M and side length a is placed at rest at the edge of a table. With half of the cube overhanging from the table, the cube begins to roll off the edge. There is sufficient friction at the edge so that the cube does not slip at the edge of the table. Find -
(a) the angle θ0 through which the cube rotates before it leaves contact with the table.
(b) the speed of the centre of the cube at the instant it breaks off the table.
(c) the rotational kinetic energy of the cube at the instant its face AB becomes horizontal.
View SolutionA flat bottomed thin-walled glass tube has a diameter of 4 cm and it weights 30 g. the centre of gravity of the empty tube is 10 cm above the bottom, find the amount of water which must be poured into the tube so that when it is floating vertically in a tank of water, the centre of gravity of the tube and its contents is at the midpoint ot the immersed length of the tube.
View SolutionConsider an ice cube of edge 1.0 cm kept in a gravity-free hall. Find the surface area of the water when the ice melts. Neglect the difference in densities of ice and water.
View SolutionAn ice cube of side 1cm is floating at the interface of kerosene and water in a beaker of base area 10cm2. The level of kerosene is just covering the top surface of the ice cube.
a. Find the depth of submergence in the kerosene and that in the water.
b. Find the change in the total level of the liquid when the whole ice melts into water.

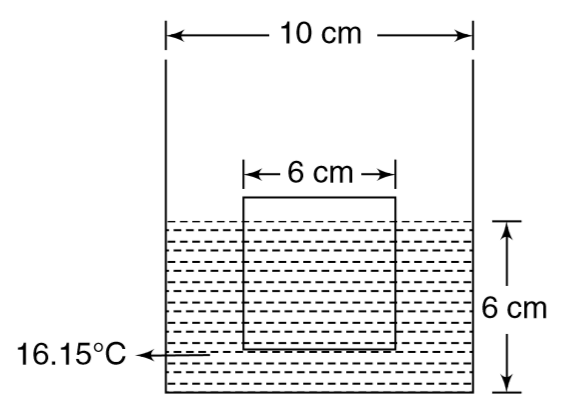
View SolutionA container has a square cross-section of 10cm×10cm. A cubical ice block of side length 6 cm is floating in water in the container. Water level in the container is 6 cm high. The ice block is at a temperature of 0∘C and the water is at 16.15∘C. Assume that heat exchange take place between the ice block and water only. What length of ice block will remain submerged in water when the system reaches thermal equilibrium? Assume that the ice block maintains its cubical shape as it melts. Take - density of ice =0.9g/cc, density of water = 1.0g/cc
Specific heat capacity of water =1calg−1.∘C−1, Specific latent heat of fusion of ice =80calg−1
View Solution
