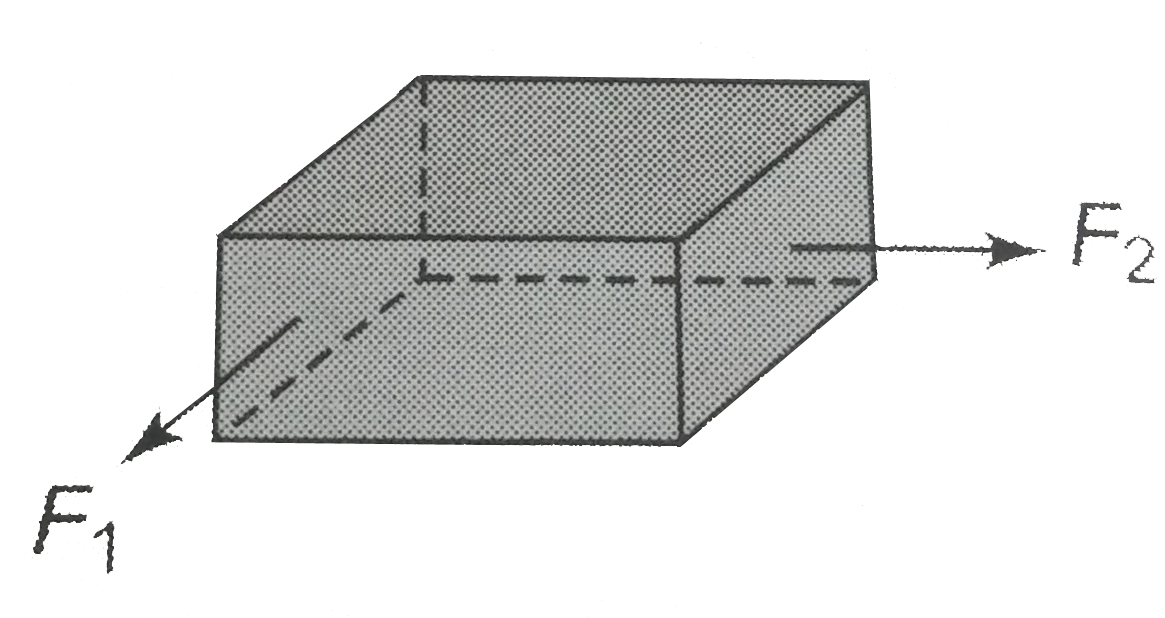
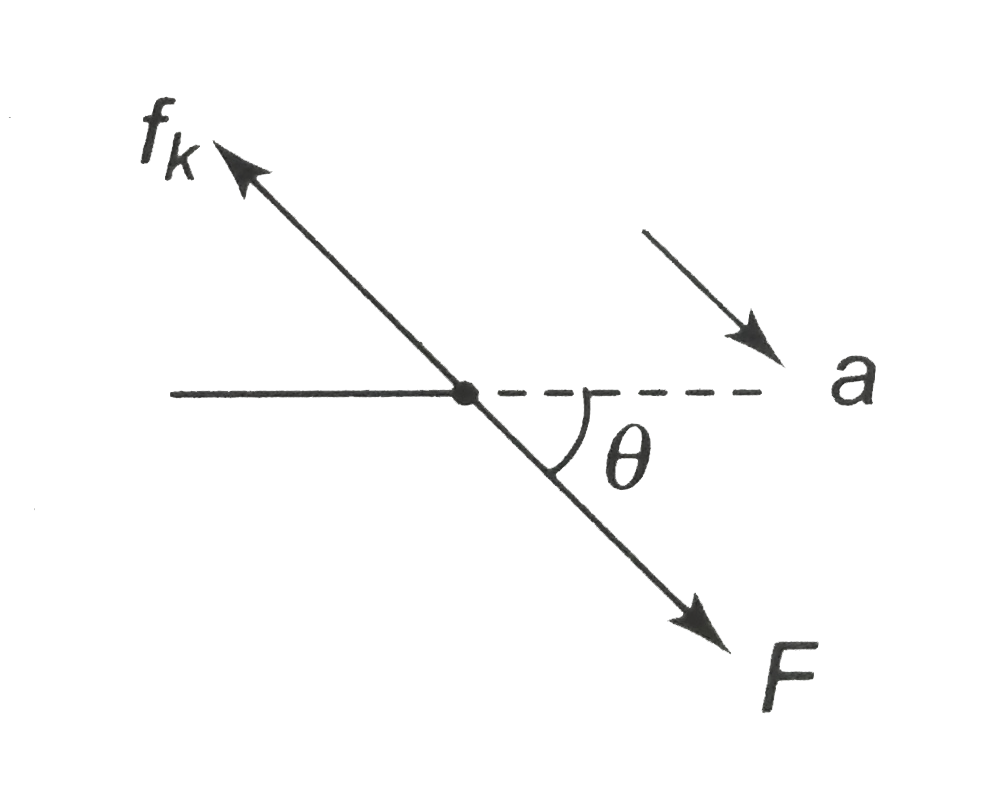
A block of mass 8kg is kept on a rough floor. The coefficients of friction are μs=0.5 and μk=0.4. Force F1=15N and F2=20N are applied on the block as shown.
(a) Find the magnitude and the direction of friction force .
(b) If F1=30N,F2=40N, find the acceleration of the block.
(a) N0=80N
(fs)max=μsN=0.5×80=40N
Resultant external force :
F=√F21+F22=√(15)2+(20)2=25N
tanθ=1520=34⇒θ=37∘
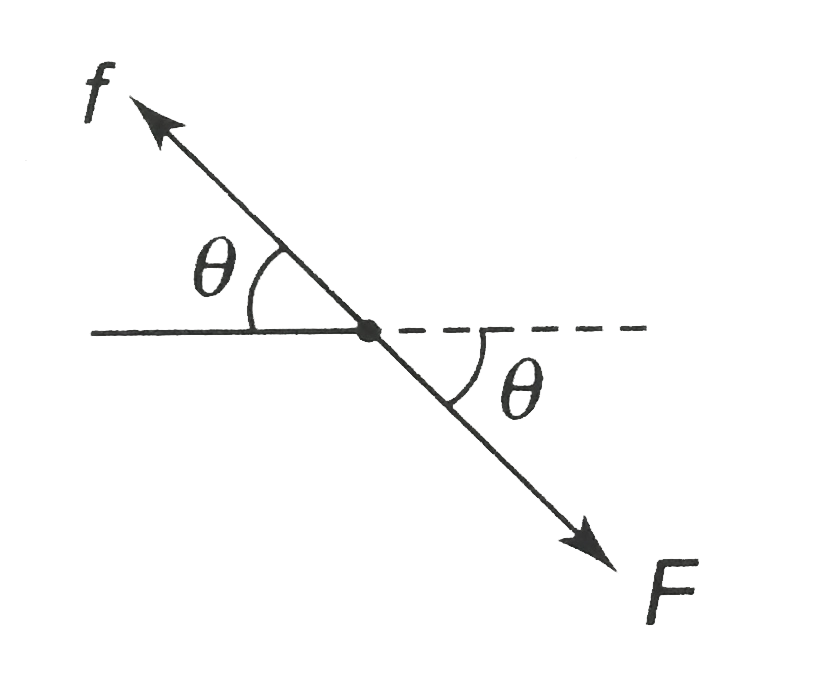
Since F<(fs)max, the block is at rest. The friction force f will act opposite to the direction of resultant force.
Friction=25N
(b) Resultant force:
F=√F21+F22=√(30)2+(40)2=50N
Now F>(fs)max , the block is in motion.
f=fk=μkN=0.4×80=32N
F−fk=ma
50−32=18a
a=188=94=2.25m/s2
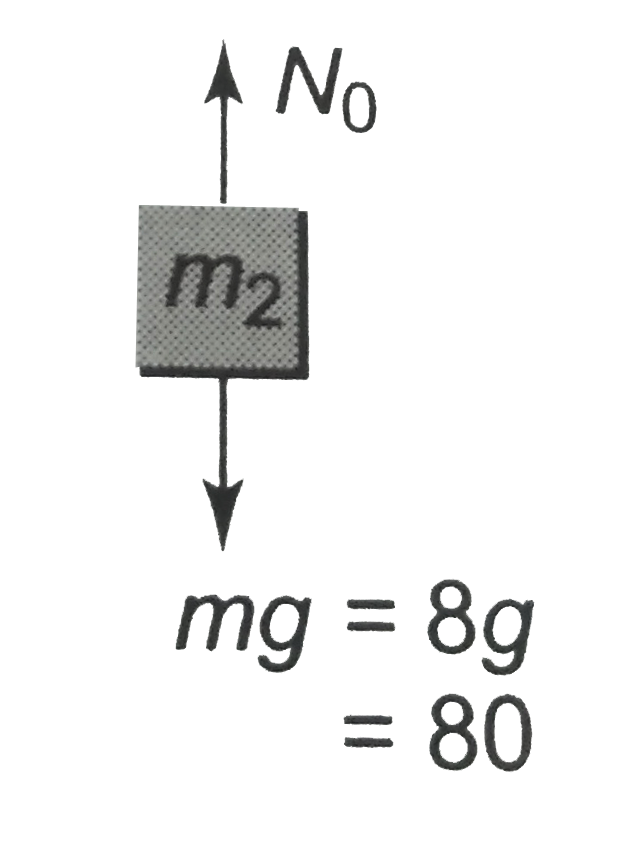
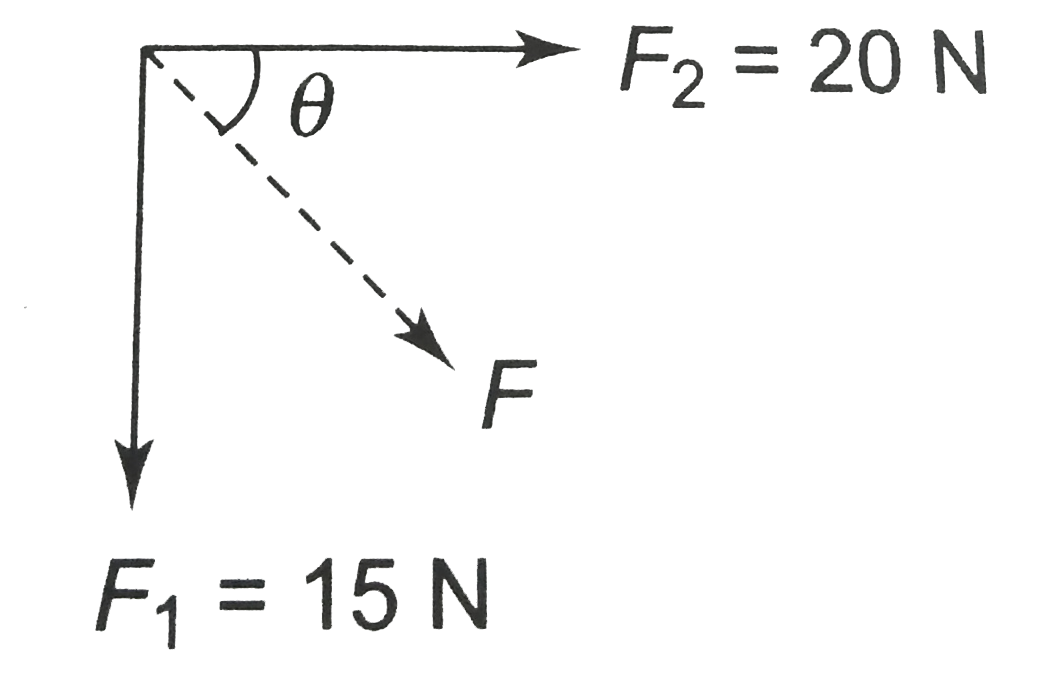
Topper's Solved these Questions
Similar Questions
A block of mass 2 kg is placed on the floor. The coefficient of static friction is 0.4.A force F of 2.5 N is applied on the block, as shown. Calculate the force of friction between the block and the floor. (g = 9.8 ms–2)
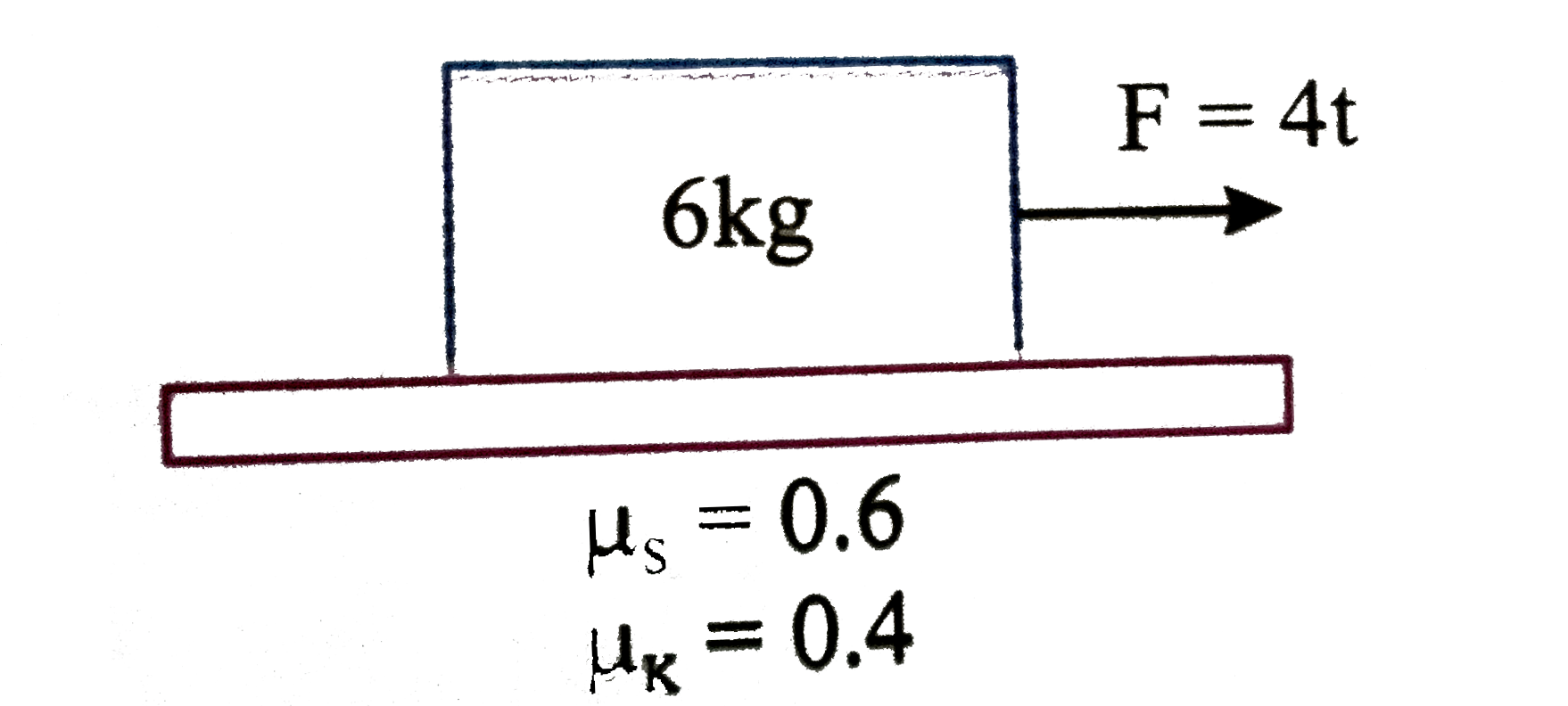
View SolutionA 6kg blocks is kept over a rough surface with coefficients of friction μs=0.6 and μk=0.4 as shown in figure. A time varying force F=4t ( F in newton and t in second) is applied on the block as shown. Find the acceleration of block at t=5sec. ( Taking g=10m/s2)
View Solution
Knowledge Check
A block of mass 10kg is kept on a rought floor .The coefficient of friction between floor and block are μs=0.4 and μk=0.3 forcesF1=5N and F2=4N are applied on the block as shown in figure
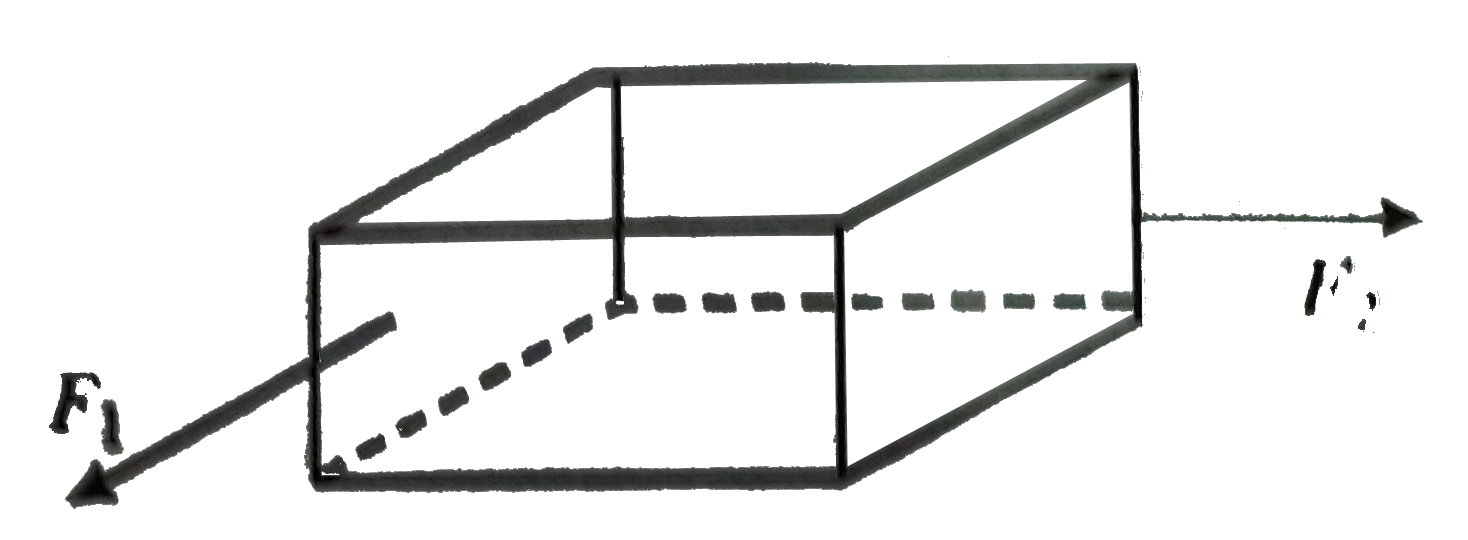
If F1=5N and F2=aN for what maximum value of a the motion of block impenride?A√1557NB√1225NC√1664ND√875NA block of mass 2kg is kept on the floor. The coefficient of static friction is 0.4 . If a force F of 2.5N is applied on the block as shown in the figure, the frictional force between the block and the floor will be.
 A2.5NB5NC7.84ND10N
A2.5NB5NC7.84ND10NA block of mass 4 kg is kept on a rough horizontal surface. The coefficient of static friction is 0.8. If a force of 19 N is applied on the block parallel to the floor, then the force of friction between the block and floor is
A32 NB18 NC19 ND9.8 N
A block of mass 5 kg is kept on a rough horizontal surface. The coefficient of friction for the contact force block and surface are μs=0⋅1andμk=0⋅9 respectively . A horizontal force F given by F 0⋅5t is applied at t = 0 . Here t represent time in seconds . Determine the force of friction and acceleration of the block at
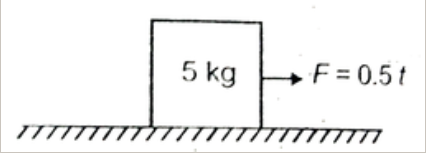
(i) t = 1s (ii) t= 10 s (iii) t = 12 s
View SolutionA block of mass 2 kg is placed on the floor. The coefficient of static friction is 0.4. A force F of 3 N is applied on the block as shown in figure. The force of friction between the block and the floor is (Take g=10ms−2)

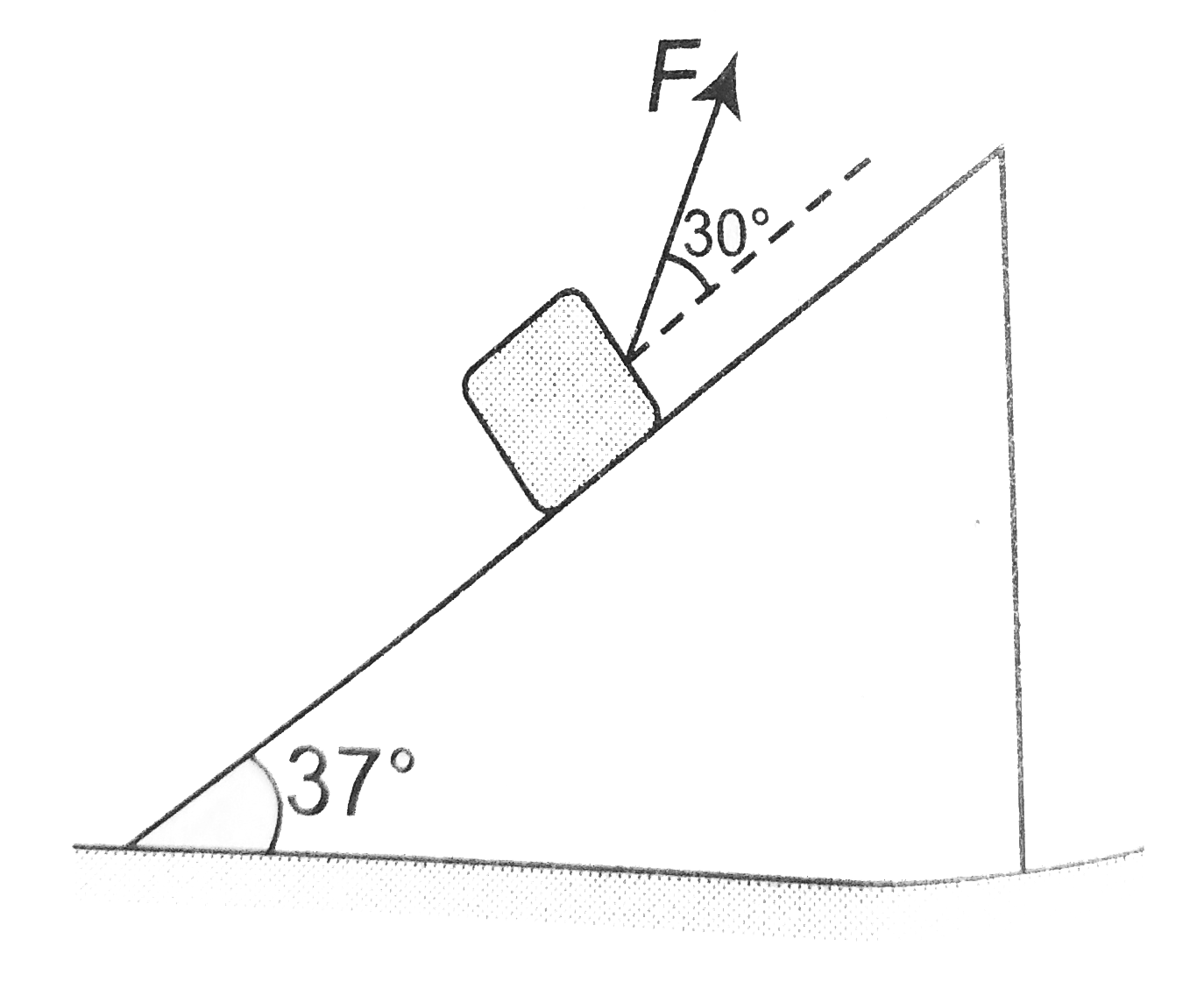
View SolutionA block of mass m=4kg is placed oner a rough inclined plane as shown in figure. The coefficient of friction between the block and the plane is μ=0.5 . A force F=10N is applied on the block at an angle of 30∘ .
View SolutionA block of mass 2 kg is kept on a rough horizontal floor an pulled with a force F. If the coefficient of friction is 0.5. then the minimum force required to move the block is :-

View SolutionA block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
View Solution
