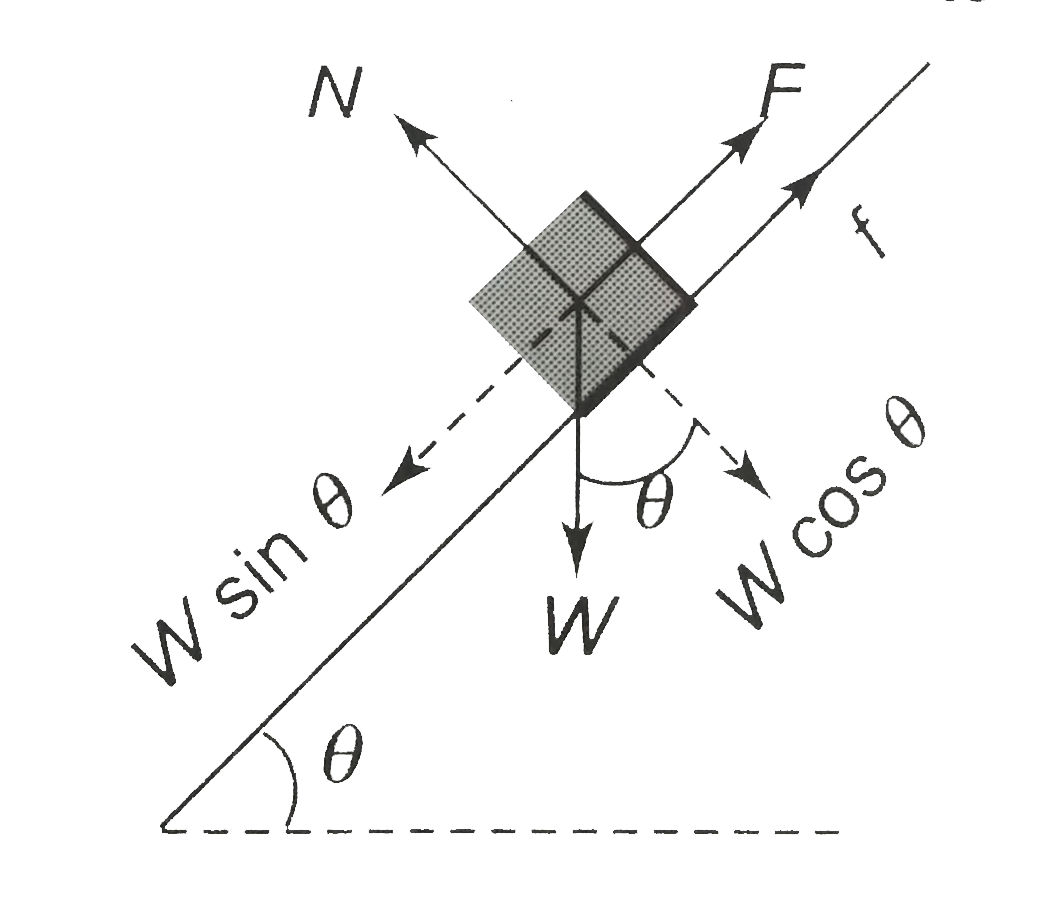
A Weight $W$ can be just supported on a rough inclined plane by a force either acting along the plane or horizontally. The angle of friction is $ϕ$ . Find the angle of inclined plane and applied force.

Video Solution

Text Solution

Verified by Experts

Let the angle of inclination of plane is $θ$ and applied force is $F$ .
When the force is acting along the plane
$⊥^{a r}$ to the plane : $N = W cos θ$
$f = μ N = μ W cos θ$
Along the plane : $F + f = W sin θ$
$F = W sin θ - μ W cos θ$
$= W sin θ - tan ϕ W cos θ [sin c w μ = tan ϕ]$
$= W (sin θ - \frac{sin ϕ}{cos ϕ} cos θ)$
$= \frac{W (sin θ cos ϕ - cos θ sin ϕ)}{cos ϕ}$
$F = \frac{W sin (θ - ϕ)}{cos ϕ}$ (i)
$⊥^{a r}$ to the plane : $N = W cos θ + F sin θ$
$f' = μ N = μ (W cos θ + F sin θ)$
Along the plane : $F cos θ + f' = W sin θ$
$F cos θ + μ (W cos θ + F sin θ) = W sin θ$
$F (cos θ + μ sin θ) = W (sin θ - μ cos θ)$
$F (cos θ + \frac{sin ϕ}{cos ϕ} sin θ) = W (sin θ - \frac{sin ϕ}{cos ϕ} cos θ)$
$\frac{F (cos θ cos ϕ + sin θ sin ϕ)}{cos ϕ} = \frac{W sin (θ - ϕ)}{cos ϕ}$
$F cos (θ - ϕ) = W sin (θ - ϕ)$
$F = \frac{W sin (θ - ϕ)}{cos (θ - ϕ)}$ (ii)
Equating (i) and (ii) , we get
$cos (θ - ϕ) = cos ϕ$
$θ - ϕ = ϕ \Rightarrow θ = 2 ϕ$
$F = \frac{W sin (θ - ϕ)}{cos ϕ} = \frac{W sin ϕ}{cos ϕ} = W tan ϕ$
Angle of inclined plane : $θ = 2 ϕ$
Applied force : $F = W tan ϕ$

Updated on:21/07/2023

A weight W can be just supported on a rough inclined place by a force F either acting along the plane or horizontally. If $θ$ is the angle of friction, then F/W is
A $tan θ$
B $sec θ$
C $sin θ$
D $cos θ$
A weight W can be just supported on a rough inclined place by a force F either acting along the plane or horizontally. If $θ$ is the angle of friction, then F/W is
A $tan ϕ$
B $sec ϕ$
C $sin ϕ$
DNone of these
A brick of mass 2kg just begins to slide down on inclined plane at an angle of $45^{\circ}$ with the horizontal. The force of friction will be
A $19.6 {sin 45}^{\circ}$
B $19.6 {cos 45}^{\circ}$
C $9.8 {sin 45}^{\circ}$
D $9.8 {cos 45}^{\circ}$