The length of second's hand in watch is 1cm. The change in Velocity of its tip in 15 seconds is
A
Zero
B
π30√2cm/sec
C
π30cm/sec
D
π√230cm/sec
Video Solution
Text Solution
The correct Answer is:D
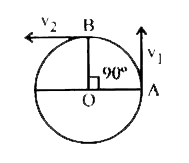
For the secong hand , T = 60 s
∴In 15 s , it will rotate through moves through 90∘
In U .C.M when the particle moves through an angle θ
the change in velocity |d→v|=2vsin(θ2)
in this case θ=90∘ and v=rωandsin(θ2)=sin45∘
∴dv=2ωsin45∘=2r(2πT)sin45∘
=2×1×2π60×1√2[∵T=60s]
∴dv=√2π30cm/s
|
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - MARVEL PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - TEST YOUR GRASP-1
1 Video
- CIRCULAR MOTIONBOOK - MARVEL PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - TEST YOUR GRASP-2
1 Video
- ATOMS, MOLECULES AND NUCLEI BOOK - MARVEL PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEI EXERCISE - TEST YOUR GRASP
30 Videos
- COMMUNICATION SYSTEMS BOOK - MARVEL PUBLICATIONCHAPTER - COMMUNICATION SYSTEMS EXERCISE - TEST YOUR GRASP -20
10 Videos
Similar Questions
Knowledge Check
The length of a seconds hand in watch is 1cm. The change in velocity of its tip in 15s is
AzeroBπ30√2cm/sCπ30cm/sDπ(√2)30cm/sThe length of second's hand in a watch is 1 cm. The change in velocity of its tip in a period of 12 s is
AZeroB(π15√2)cms−1C(π15)cms−1D(π√2)15⎞⎟ ⎟⎠cms−1The angular speed of second hand in a watch is
Aπ60rad/sBπ30rad/sCπ120rad/sDπ2rad/s
The angular velocity of second's hand of a watch will be.
View SolutionIf the length of the second's hand in a stop clock is 3 cm the angular velocity and linear velocity of the tip is
View SolutionThe angular velocity of the seconds hand in a watch is
View SolutionIf the length of second's hand of a clock is 10 cm, the speed of its dip (in cms−1) is nearly
View SolutionIf the length of second's hand of a clock is 10cm , the speed of its dip (in cm−1)is nearly .
View Solution
