Non-inertial frame of reference have
zero acceleration.
some acceleration with respect to inertial frame of reference.
zero velocity.
constant velocity with respect to inertial frame of reference.
The correct Answer is:B
Step by step video, text & image solution for Non-inertial frame of reference have by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FORCE BOOK - TARGET PUBLICATIONCHAPTER - FORCE EXERCISE - Classical Thinking (4.6 Moment of force)
5 Videos
- FORCE BOOK - TARGET PUBLICATIONCHAPTER - FORCE EXERCISE - Classical Thinking (4.7 Couple and properties of couple)
8 Videos
- FORCE BOOK - TARGET PUBLICATIONCHAPTER - FORCE EXERCISE - Classical Thinking (4.4 Elastic and inelastic collision in one and two dimensions)
10 Videos
- ELECTRONS AND PHOTONSBOOK - TARGET PUBLICATIONCHAPTER - ELECTRONS AND PHOTONSEXERCISE - Evaluation Test
19 Videos
- FRICTION IS SOLIDS AND LIQUIDS BOOK - TARGET PUBLICATIONCHAPTER - FRICTION IS SOLIDS AND LIQUIDS EXERCISE - MCQ (EVALUATION TEST)
21 Videos
Similar Questions
Assertion: The driver in a vechile moving with a constant speed on a straight road is in a non-inertial fram of reference.
Reason: A reference frame in which Newton's law of motion are applicable is non-inertial.
View SolutionAssertion: For the object moving on the earth, earth is non-inertial frame of reference.
Reason: Newton's first law of motion does hot hold good for the earth.
View Solution
Knowledge Check
Statement I: A concept of pseudo force is valid both for inertial as well as non-inertial frame of reference.
Statement II: A frame accelerated with respect to an inertial frame is a non-inertial frame.AStatement I is true, statement II is true, Statement II is the correct explanation for statement I.BStatemet I is true, Statement II is true , Statement II is NOT the correct explanation for Statement ICStatement I is True, Statement II is False.DStatement I is False, Statement II is trueIn an inertial frame of reference, the magnetic force on a moving charged particle is F. Its value in another inertial frame of reference will be
Aremained sameBchanged due to change in the amount of chargeCchanged due to change in velocity of charged particleDchanged due to change in field directionIn order to apply Newton's law of motion in an accelerated (non-inertial ) frame of reference, we make the use fo
Aelectrostatic forceBgravitationa forceCpseudo forceDelectromagnetic force
Assertion: We can apply τ=Iα about the centre of mass of the system in non-inertial frame of reference.
Reason: Torque of pseudo forces about centre of mass is zero
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
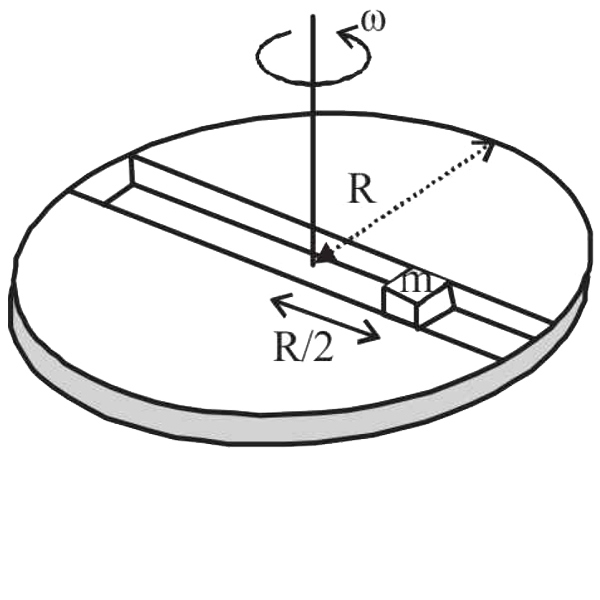
The distance r of the block at time is
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
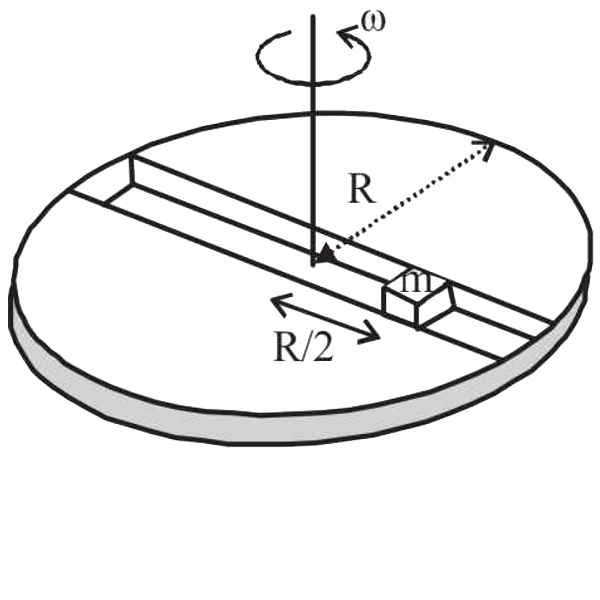
The net reaction of the disc on the block is
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionIn an inertial frame of reference, a body performing uniform circular motion in clockwise direction has
View Solution
