If and α-paricle of mass m, charged q and velocity v is incident on a nucleus charge Q and mass m, then the distance of closest approach is
Qq4πε0m2v2
Qq2πε0mv2
Qqmv22
Qqmv2
The correct Answer is:B
Distance of closest approach,
r0=Zke2KE=qQ4πε01/2mv2=qQ2πε0mv2
Topper's Solved these Questions
- ATOMS, MOLECULES AND NUCLEI Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:ATOMS, MOLECULES AND NUCLEI Exercise:Exercise 2 (MISCELLANEOUS PROBLEMS)
Explore 26 Videos
- ATOMS, MOLECULES AND NUCLEI Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:ATOMS, MOLECULES AND NUCLEI Exercise:MHT CET Corner
Explore 30 Videos
- ATOMS, MOLECULES AND NUCLEI Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:ATOMS, MOLECULES AND NUCLEI Exercise:MHT CET Corner
Explore 30 Videos
- CIRCULAR MOTIONBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:CIRCULAR MOTIONExercise:MHT CET CORNER
Explore 21 Videos
Similar Questions
A charged particle of mass m and charge q is kept initially at rest on a frictionless surface. Another charged particle of mass 4m and charge 2q starts moving with velocity v towards it. Calculate the distance of the closest approach for both the charged particles.
View SolutionFigure shows a charge +Q clamped at a point in free space. From a large distance another charge particle of charge -q an.d mass m is thrown toward +Q with an impact parameter d as shown with speed v. Find the distance of closest approach of the two particles.
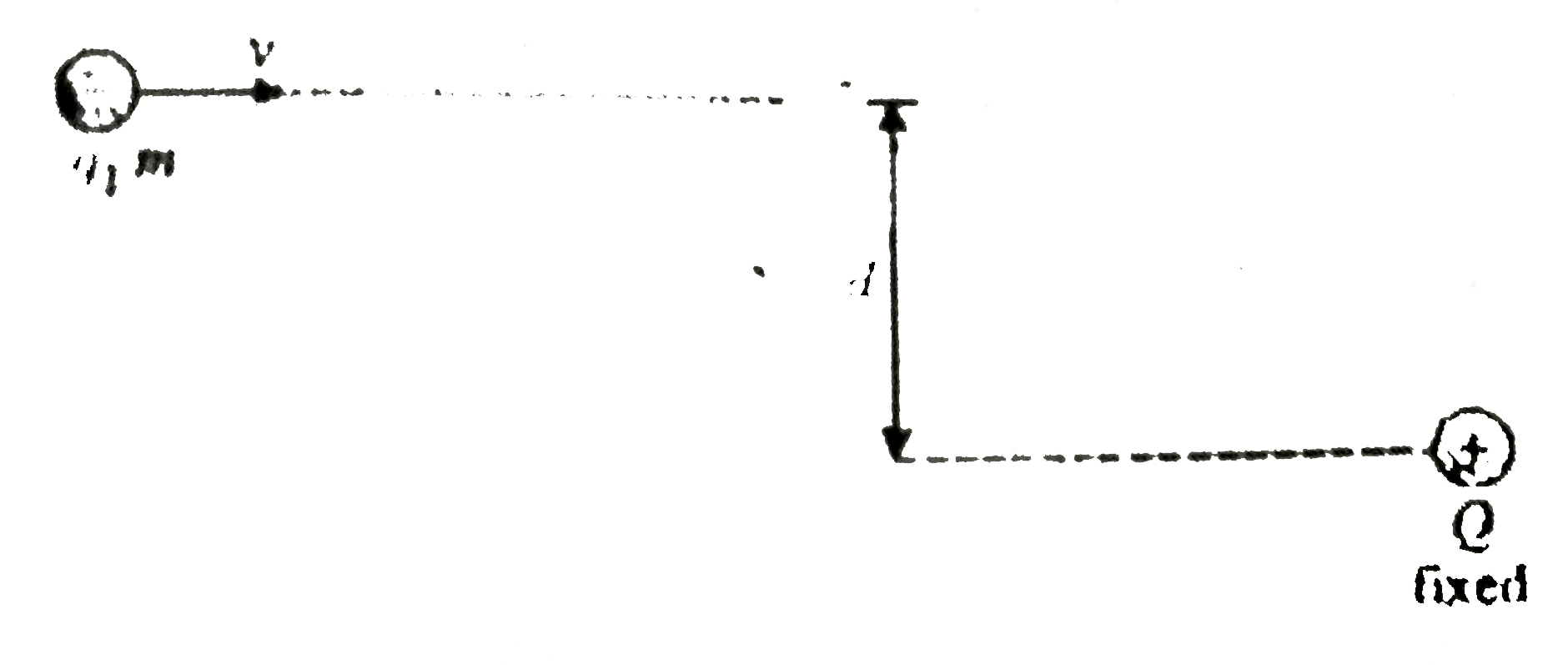
View Solution
Knowledge Check
When an α particle of mass m moving with velocity v bombards on a heavy nucleus of charge Ze, its distance of closest approach form the nucleus depends on m as
A1√mB1m2CmD1mWhen an α−particle of mass 'm' moving with velocity 'v' bombards on a heavy nucleus of charge 'Ze' its distance of closest approach from the nucleus depends on m as :
AmB1mC1√mD1m2When an a-particle of mass 'm' moving with velocity 'v' bombards on a heavy nucleus of charge 'Ze', its distance of closest approach from the nucleus depends on v as:
A1vB1√vC1v2Dv
An alpha particle of velocity 1.6×107ms−1 approaches a gold nucleus (Z=79). Calculate the distance of the closest approach. Mass of an alpha particle is 6.6×10−27 kg. What is the significance of this closest approach?
View SolutionIn a Rutherford scattering experiment when a projectile of charge Z1 and mass M1 approaches a target nucleus of charge Z1 and mass M2 , the distance of closest approach is r0 . The energy of the projectile is .
View SolutionWhen an α particle of mass m moving with velocity v bombards on a heavy nucleus of charge Ze, its distance of closest approach form the nucleus depends on m as
View SolutionIf an α-particle is incident directly towards a nucleus then it will stop when the distance between them is the distance of closest approach. Which of these is correct?
View SolutionA beam of specific kind of particles of velocity 2.1×107m/s is scattered by a gold (Z=79) nuclei. Find out specific charge (charge/mass) of this particle if the distance of closest approach is 2.5×10−14m.
View Solution

